Burnside引理与polya定理

1、置换

　　置换简单来说就是对元素进行重排列，如下图所示。置换是[1,n]到[1,n]的一一映射。

　　举个直观的例子，将正方形绕其中心逆时针旋转90度，可以看成是正方形四个顶点的一个置换。关于置换、置换群的具体理论，请参考其他资料，此处有个大致印象就好。下面描述几个结论。 

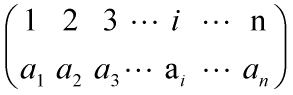
　　（1）置换可以分解成若干循环，方法为：连边1->a₁,2->a₂,…，i->a_i，…,n->a_n，任取一个元素，顺着有向边走，直到回到出发点，即形成一个环，剩余元素如法炮制。

　　（2）如果一个状态经过置换 f 后跟原来相同，即S[1] = S[a₁], S[2] = S[a₂], …, S[n] = S[a_n]。则称该状态为 f 的不动点。

　　（3）题目中常常出现“本质不同的方案数”，一般是指等价类的数目，题目定义一个等价关系，满足等价关系的元素属于同一等价类。等价关系通常是一个置换集合F，如果一个置换能把其中一个方案映射到另一个方案，则二者是等价的。

2、burnside引理

　　对于一个置换f,若一个染色方案s经过置换后不变，称s为f的不动点。将f的不动点数目记为C(f)，则可以证明等价类数目为所有C(f)的平均值。

 

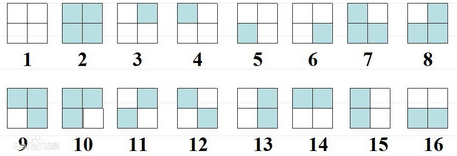
　　如上图（图片来自百度百科“burnside引理”）所示，对于四个置换{逆时针旋转0°,逆时针旋转90°,逆时针旋转180°,逆时针旋转270°}，其不动点数分别为16, 2, 4, 2。所以等价类数目为(16+2+4+2)/4 = 6。

3、polya定理

 　　polay定理实际上是burnside引理的具体化，提供了计算不动点的具体方法。

　　假设一个置换有k个循环，易知每个循环对应的所有位置颜色需一致，而任意两个循环之间选什么颜色互不影响。因此，如果有m种可选颜色，则该置换对应的不动点个数为m^k。用其替换burnside引理中的C(f)，得到等价类数目为：

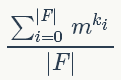
　　其中|F|表示置换的数目，k_i表示第i个置换包含的循环个数。 

4、例题

// LA_3641 Leonardo's Notebook
#include <cstdio>
using namespace std;

int main()
{
    int T;
    char B[30];
    int c[30];
    bool v[30];
    scanf("%d", &T);
    while(T--)
    {
        scanf("%s", B);
        for(int i = 0; i <= 26; i++) c[i] = 0, v[i] = 0;
        for(int i = 0; i < 26; i++){
            if(v[i] == 0) {
                v[i] = 1;
                int t = 1, j = B[i]-'A';
                for(; j != i; j = B[j]-'A') t++, v[j] = 1;
                c[t]++;
            }
        }
        bool flag = true;
        for(int i = 2; i <= 26; i += 2) if(c[i]&1) flag = false;
        puts(flag ? "Yes" : "No");
    }
    return 0;
}

// LA_3510 Pixel Shuffle
#include <cstdio>
#include <cctype>
#include <cstring>
using namespace std;

char oper[35][10];

const int maxn = 1024;

int ori[maxn*maxn];
#define ID(i, j) ((i)*n+(j))//注意这样定义函数的时候，一定不要偷懒，省略任意一个括号，都可能产生致命的后果


int NewPos(int i, int j, int n, char *op)
{
    if(op[0] == 'i') return ID(i, j);
    if(op[0] == 'r') return ID(n-1-j, i);
    if(op[0] == 's') return ID(i, n-1-j);
    if(op[0] == 'b' && op[1] == 'h') return (2*i >= n) ? ID(i, n-1-j) : ID(i, j);
    if(op[0] == 'b' && op[1] == 'v') return (2*i >= n) ? ID(n/2+n-i-1, j) : ID(i, j);
    if(op[0] == 'd') return (i&1) ? ID(n/2+i/2, j) : ID(i/2, j);
    if(op[0] == 'm') {
        int k = (i>>1)<<1;
        if(j < n/2) return ID(k, (j<<1)+(k!=i));
        else {
            j -= n/2;
            return ID(k+1, (j<<1)+(k!=i));
        }
    }
}

void apply(int* image, int n, char *op)//维护一个当前的序列
{
    bool div = 0;
    if(op[strlen(op)-1] == '-') div = 1;
    for(int i = 0; i < n*n; i++) ori[i] = image[i];
    int mx = -1, mi = -1;
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++){
            int p = ID(i, j), p2 = NewPos(i, j, n, op);
            if(div) image[p] = ori[p2];
            else image[p2] = ori[p];
        }
    }
}

bool v[maxn*maxn];

int gcd(int x, int y) { return y == 0 ? x : gcd(y, x%y);}
int lcm(int x, int y) { return x/gcd(x, y)*y; }

int solve(int* image, int n)//对于给定的置换，计算其各个循环长度的最小公倍数
{
    int ans = 1;
    for(int i = 0; i < n; i++) v[i] = 0;
    for(int i = 0; i < n; i++){
        if(!v[i]){
            v[i] = 1;
            int c = 1, j = image[i];
            for( ; j != i; j = image[j]) c++, v[j] = 1;
            ans = lcm(ans, c);
        }
    }
    return ans;
}
int cur[maxn*maxn];
int main()
{
    int T, n;
    scanf("%d %d", &T, &n);
    while(T--)
    {
        int c = 0, n1;
        while(~scanf("%s", oper[c]))
        {
            if(isdigit(oper[c][0])){
                sscanf(oper[c], "%d", &n1);
                break;
            }
            c++;
        }
        for(int i = 0; i < n*n; i++) cur[i] = i;
        for(int i = c-1; i >= 0; i--)
            apply(cur, n, oper[i]);
        printf("%d
", solve(cur, n*n));
        if(T) puts("");
        n = n1;
    }
    return 0;
}