最近很累 南昌打铁 选拔赛打的一塌糊涂 没有心态了 颓了好久 今天写写st表
首先 RMQ(Range MIinimum/Maximum Query 离线查询区间最大最小值)
有很多种写法比如线段树(蔡) 树状数组(不会) st表
那么来讲讲st表
首先st表的主体其实就是一个预处理的数组
预处理时间复杂度o(nlogn) 查询时间复杂度o(1) 空间复杂度o(n)
首先我们来看预处理代码 然后根据代码讲解st表的
for (int i = 1; i <= n; i++) cin >> f[i][0]; for (int j = 1; j <= 20; j++) for (int i = 1; i <= n; i++) if (i + (1 << j) - 1 <= n) f[i][j] = min(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
如果一个区间i的长度为1,那么f[i][0]就为位置i对应的值 对于一个长度为2的区间a—>b,
我们可以用f[a][1]来表示这个区间的极值,那么对于这个区间而言,
f[a][1]的最小值就可以看做min(a,b),即可以看做min(f[a][0],f[a+(1<<0)][0])。
如果我们把 左端点记做i,区间长度改为j呢 那么f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1];
所有我们在预处理的时候,我们不妨先枚举区间长度j,再枚举区间左端点i。
只要能保证i+(1<<j)-1≤n,那么我们便可以将各种区间给预处理出来。

(偷luogu的图)
那么预处理完了 怎么才能做到o(1)查询呢
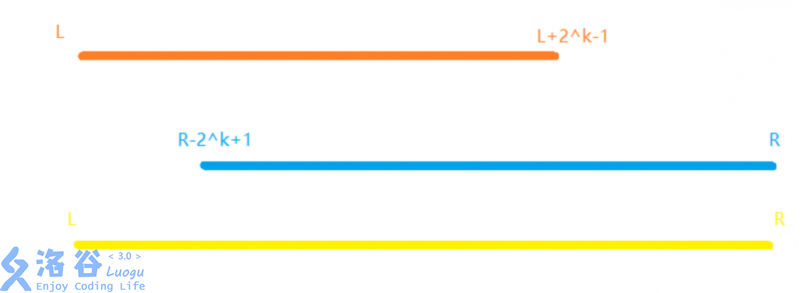
因为无法做到输入的l与r一定是2的次方数 所以无法做到精准查询 不过我们看上图 可以发现 要查询的区间可以通过两个区间的并集来得到
所以我们有代码
int check(int l, int r) { int z = log2(r - l + 1); return min(f[l][z], f[r - (1 << z) + 1][z]); }
这样我们就做到了o(1)的查询