Clustering by Passing Messages Between Data Points(Brendan J.Frey* and Delbert Dueck)译文与认识
原创文章，禁止转载
摘要：在处理感知信号和检测数据中的模式中，通过识具有代表性的例子进行数据聚类是十分重要的，这样的exemplars可以通过随机选择初始化数据集合，然后迭代精炼该集合，该方法仅仅在随机选择接近于一个良好的解时是很有用的。我们提出一种方法叫做affinity propagation，其将成对数据间的的相似性度量作为输入。数据之间交换实值消息，直到一个高质量exemplars的集合和其对应的簇逐渐产生。我们使用affinity propagation在人脸的图像分类，微阵列数据中检测基因，识别本原稿中代表性的句子，识别在航空旅行中可以获得的有效城市。Affinity propagation在相比其他方法上找到更低误差的簇，并且花费不到百分之一的时间（与其他方法比较）。
正文
基于相似性度量的数据聚类是在数据分析和工程系统中一种重要的手段。一种常用的方法是使用数据去学习一系列的中心点，该中心点使得数据与最邻近的中心点的平法误差和最小，当中心点选择为实际数据时，这些选择的数据中心实例点叫做exemplars。流行的k-centers聚类技术就是开始于一些随机exemplars，然后以减少误差平方和为目标来进行迭代精炼该集合。k-centers聚类对于初始选择的exemplars十分敏感！通常需要重新计算很多不同初始化情况试图找到最优的解。然而这种方法只在聚类规模小，并且初始化靠近一个良好的解时，效果良好。我们现在用不同的方法并且介绍一种方法：同时考虑所有的点作为潜在的exemplars，把所有的数据点视为网络中的结点，我们设计一种方法，伴随着网络中的边递归的传递实值消息，直到一个良好exemplars的集合和对应的簇出现。正如稍后描述的那样，消息更新基于简单的公式，搜索一个恰当选择能量函数的最小值。在任何时间点，每一个消息的大小反映了一个数据点选择另一个数据点作为它exemplar的当前affinity（亲和力，吸引力）。所以我们把我们的方法叫做“affinity propagation”，图1A表示在消息传递过程中，簇是如何逐步产生的。
AP把数据点之间实值的相似度作为输入，相似度s(i，k)表示多大程度上k索引的数据点适合作为数据点i的exemplar。当目标是最小化平方误差时，每一个相似度设定为负的平方误差（欧几里得距离）。对于点xi和xk,
，确实，这里描述的方法可以应用到优化准则更加一般的情况下，随后，我们描述的工作：相似度来自是成对图像、成对微阵列测量测量、成对的英语句子、成对的城市。当exemplar依赖的概率模型是可以得到的时候，s(i，k)可以设定为给定数据点i的exemplar为k时，数据点i的对数似然函数。或者，在恰当的时候，相似度可以手动设定。
AP把实数s(k，k)作为每一个数据点k的输入，而不并不需要预先设定簇的数目。那些具有更大s(k，k)的数据点，具有更大的可能被选作一个exemplar。这些值（即输入的s(k，k)）被叫做preferences（参考度）。识别exemplars的数目（簇的数目）受到输入参考度的影响，在消息传递过程中慢慢浮现。假使有一个先验，所有数据点都是同等适合作为exemplars，那么参考度应该设定为同大小的值——这个值的改变可以引起不同类别数，该值可以设定为输入相似度的中值（产生适中的簇数目）或者他们的最小值（产生一个小数量的簇数目）。
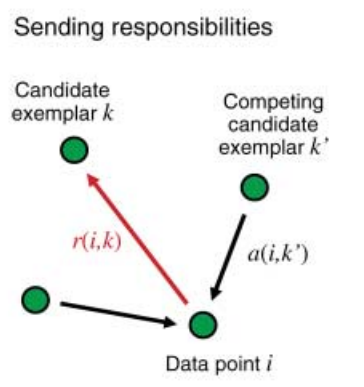
这里数据点有两种消息交换，每一种考虑不同的竞争。消息在每一个阶段可以被结合起来决定哪个点作为exemplars，对每一个其他点，它属于哪个exemplar。responsibility r(i，k)，从点i发送消息到点k，考虑i的其他候潜在选exemplars，反映k适合作为点i的exemplar的累积证据。
补充： 在一个亲子关系的分析时，我看到对于responsibility和availability的一些解释，我认为能够帮助理解这两个消息的含义。
尽责程度responsibility：父亲在抚养孩子时，在多大程度上去满足孩子成长所需要的资源要求，包括物质资源和其他无形的资源。
（r(i，k)有两部分组成，其中s(i，k)为k作为i的exemplar的适合程度，是不是就可以理解为k能够满足表达i的程度，另一部分是其他候选exemplar点k’对于i表达程度与可及程度之和，作减法体现出k相对于k’来说，在表达i的时候呈现的竞争优势）
可及程度availability：父亲对于孩子来说，可以潜在地“触及”或者“得到”的程度，孩子觉得自己需要父亲时，能够多大程度上得到对于对方的支持与回应。
（a(i，k)的理解还不完全，先看做k作为自身exemplar的累积证据加上从其他点得到k为exemplar的累积证据，k对于自身的尽责程度加上k对于其他点的优势表达程度反映k对于i的可及程度（？为什么是对于别人的优势表达和作为自身的exemplar能够体现出可及程度？对别的点优势表达程度明显，又十分适合作为自身的exemplar，这样传递给i点什么意思呢？我能够很好的表达其他点，自身有自信，所以也适合你选择我是合适的），即k传递给i，自己能够给予的回应程度）
availability，a(i,k)从候选exemplar点k传递给点i，反映的是考虑来自其他点对k应该成为一个exemplar的支持，i选择k作为exemplar的合适程度。
r(i，k)和a(i，k)可以看做对数概率的比率。
- 初始，a(i，k)初始化为0，即a(i，k)=0
- responsibility的计算使用下面的规则
- 由于a(i，k)=0，r(i，k)设定为k作为i的exemplar的输入相似度减去i与其他候选exemplar的最大相似度，这个计算更新是数据驱动的，而不考虑有多少其他的数据点对每一个exemplar的赞成。
- 随后的迭代中，一些数据点被有效的分配给其他exemplars，这时它们的availability就会如同下面的更新规则中描述的那样，下降到0以下。这些负的availability会减少上面更新规则中一些输入的相似度s(i，k’)的有效值，在竞争中，移去对应候选exemplar的力量。
- 对于k=i，responsibility r（k，k）设定为输入参考度s(k，k)减去i与其他候选exemplar的最大相似度，这种self-responsibility，反映k作为一个exemplar的累积证据，基于通过将它分配其他exemplar有多么不合适来调节其输入参考度。
- 上面r(i，k)的更新，即让所有的候选exemplars竞争对于数据点的所有权（ownership）
- 下面a(i，k)的更新，对于每一个候选exemplar，从数据点搜集其是否可以成为一个好的exemplar的证据。
-
a(i，k)设定为self-responsibility加上候选exemplar点k从其他数据点接收到的正的responsibility。只有进来的responsibility的正的部分被加，因为只需要一个好的exemplar能够很好的解释一些数据点（positive responsibility），忽略它对于解释其他数据点（negative responsibility）是多么不充分。
- self-responsibility r(k，k)如果为负的话（表示点k当前最好属于另一个exemplar，而不是以自身为exemplar）。在一些数据点选择k为exemplar的时候获得正的responsibility（k具有更强的竞争能力，在表达这些数据点具有很好的效果）时，k作为一个exemplar的availability会增加。
- 为了限制进来positive responsibility的强大影响，整个和的阈值不会超过0。
- self-availability a(k，k)更新规则如下，基于其他数据点传送给候选exemplar点k的正的responsibility，反映k作为一个exemplar的累积证据。
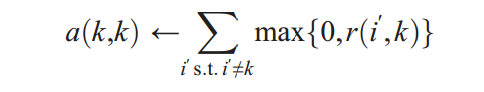
- 上面的更新规则只需要简单的局部计算，并且容易实现，消息只在已知相似度的成对结点之间交换。
- 在AP过程中，每一个点使用availability和responsibility结合鉴别exemplars。
- 对于点i来说，不论k=i与否，使得a(i,k)+r(i,k)取值最大的那个k即为点i的exemplar。
- 消息传递过程终止于一个固定的迭代次数，或者消息的变化下降到一个阈值，或者局部决定在一定迭代次数中为常量。
- 在更新消息时，使他们衰减，从而避免在某些情况下数值震荡。每一个消息设定为前一次消息的λ倍加上（1-λ）倍指定的更新值，阻尼因子λ取值为0到1之间，在我们所有的实验中，我们取默认阻尼因子λ为0.5。
- 每一次迭代包括（i）在给出availability的情况下更新所有的responsibility
（ii）在给出responsibility的情况下更新所有的availability
（iii）结合availability和responsibility监控exemplar决定和在这些决定在10次迭代中均不再改变时，迭代终止算法