Codeforces Round #273 (Div. 2)

联系:http://codeforces.com/contest/478

A. Initial Bet

time limit per test

1 second

memory limit per test

256 megabytes

There are five people playing a game called "Generosity". Each person gives some non-zero number of coinsb as an initial bet. After all players make their bets ofb coins, the following operation is repeated for several times: a coin is passed from one player to some other player.

Your task is to write a program that can, given the number of coins each player has at the end of the game, determine the sizeb of the initial bet or find out that such outcome of the game cannot be obtained for any positive number of coinsb in the initial bet.

Input

The input consists of a single line containing five integersc₁, c₂, c₃, c₄ andc₅ — the number of coins that the first, second, third, fourth and fifth players respectively have at the end of the game (0 ≤ c₁, c₂, c₃, c₄, c₅ ≤ 100).

Output

Print the only line containing a single positive integerb — the number of coins in the initial bet of each player. If there is no such value ofb, then print the only value "-1" (quotes for clarity).

Sample test(s)

Input

2 5 4 0 4

Output

3

Input

4 5 9 2 1

Output

-1

Note

In the first sample the following sequence of operations is possible:

1. One coin is passed from the fourth player to the second player;
2. One coin is passed from the fourth player to the fifth player;
3. One coin is passed from the first player to the third player;
4. One coin is passed from the fourth player to the second player.

分析: 签到，注意0的时候特判－1

#include <cstdio>
int main()
{
    int a, b, c, d, e;
    scanf("%d %d %d %d %d", &a, &b, &c, &d, &e);
    int sum = a + b + c + d + e;
    if(sum == 0)
        printf("-1
");
    else if(sum % 5 == 0)
        printf("%d
", sum / 5);
    else
        printf("-1
");
}

B. Random Teams

time limit per test

1 second

memory limit per test

256 megabytes

n participants of the competition were split intom teams in some manner so that each team has at least one participant. After the competition each pair of participants from the same team became friends.

Your task is to write a program that will find the minimum and the maximum number of pairs of friends that could have formed by the end of the competition.

Input

The only line of input contains two integers n and m, separated by a single space (1 ≤ m ≤ n ≤ 10⁹) — the number of participants and the number of teams respectively.

Output

The only line of the output should contain two integersk_min andk_max — the minimum possible number of pairs of friends and the maximum possible number of pairs of friends respectively.

Sample test(s)

Input

5 1

Output

10 10

Input

3 2

Output

1 1

Input

6 3

Output

3 6

Note

In the first sample all the participants get into one team, so there will be exactly ten pairs of friends.

In the second sample at any possible arrangement one team will always have two participants and the other team will always have one participant. Thus, the number of pairs of friends will always be equal to one.

In the third sample minimum number of newly formed friendships can be achieved if participants were split on teams consisting of2 people, maximum number can be achieved if participants were split on teams of1, 1 and 4 people.

分析: 贪心。最大值显然是n－m＋1人为一组。最小值则是尽可能均分，均分的话将余数均分分别加到商上就可以

#include <cstdio>
#define ll long long

ll cal(ll x)
{
    return x * (x - 1) / 2;
}

int main()
{
    ll n, m;
    ll ma, mi;
    scanf("%I64d %I64d", &n, &m);
    ma = cal(n - m + 1);
    ll tmp = n % m;
    ll a = n / m;
    ll num = 0;
    if(tmp == 0)
        mi = m * cal(a);
    else
        mi = tmp * cal(a + 1) + (m - tmp) * cal(a);
    printf("%I64d %I64d
", mi, ma);
}

C. Table Decorations

time limit per test

1 second

memory limit per test

256 megabytes

You have r red,g green and b blue balloons. To decorate a single table for the banquet you need exactly three balloons. Three balloons attached to some table shouldn't have the same color. What maximum number t of tables can be decorated if we know number of balloons of each color?

Your task is to write a program that for given valuesr, g andb will find the maximum number t of tables, that can be decorated in the required manner.

Input

The single line contains three integers r, g and b (0 ≤ r, g, b ≤ 2·10⁹) — the number of red, green and blue baloons respectively. The numbers are separated by exactly one space.

Output

Print a single integer t — the maximum number of tables that can be decorated in the required manner.

Sample test(s)

Input

5 4 3

Output

4

Input

1 1 1

Output

1

Input

2 3 3

Output

2

Note

In the first sample you can decorate the tables with the following balloon sets: "rgg", "gbb", "brr", "rrg", where "r", "g" and "b" represent the red, green and blue balls, respectively.

分析:大概写几个yy一下

#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;

int main()
{
    ll a[3], ans = 0;
    scanf("%I64d %I64d %I64d", &a[0], &a[1], &a[2]);
    sort(a, a + 3);
    if((a[0] + a[1]) <= a[2] / 2)
        ans = a[0] + a[1];
    else
        ans = (a[0] + a[1] + a[2]) / 3;
    printf("%I64d
",ans);
}

D. Red-Green Towers

time limit per test

2 seconds

memory limit per test

256 megabytes

There are r red andg green blocks for construction of the red-green tower. Red-green tower can be built following next rules:

• Red-green tower is consisting of some number of levels;

• Let the red-green tower consist of n levels, then the first level of this tower should consist of n blocks, second level — of n - 1 blocks, the third one — ofn - 2 blocks, and so on — the last level of such tower should consist of the one block. In other words, each successive level should contain one block less than the previous one;

• Each level of the red-green tower should contain blocks of the same color.

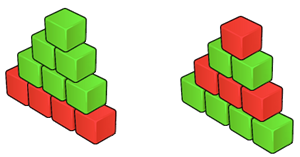
Let h be the maximum possible number of levels of red-green tower, that can be built out ofr red and g green blocks meeting the rules above. The task is to determine how many different red-green towers havingh levels can be built out of the available blocks.

Two red-green towers are considered different if there exists some level, that consists of red blocks in the one tower and consists of green blocks in the other tower.

You are to write a program that will find the number of different red-green towers of heighth modulo 10⁹ + 7.

Input

The only line of input contains two integers r and g, separated by a single space — the number of available red and green blocks respectively (0 ≤ r, g ≤ 2·10⁵,r + g ≥ 1).

Output

Output the only integer — the number of different possible red-green towers of heighth modulo 10⁹ + 7.

Sample test(s)

Input

4 6

Output

2

Input

9 7

Output

6

Input

1 1

Output

2

Note

The image in the problem statement shows all possible red-green towers for the first sample.

分析 :dp。算下高度，然后算出r的最小须要的个数，高度i。1-h枚举。红色j。r－0枚举dp[j] += dp[j - i]；最后把满足条件的dp值加起来就可以

#include <cstdio> 
#include <cstring>
#define ll long long   
int const MOD = 1e9 + 7;
int const MAX = 200000 + 5;
int dp[MAX];

int main()
{
    int r, g, h, ans = 0, tmp = 0;
    scanf("%d %d", &r, &g);
    ll min_r;
    memset(dp, 0, sizeof(dp));
    dp[0] = 1;
    for(int i = 1; tmp <= (r + g) ;i++)
    {
        tmp += i;
        if(tmp > (r + g))
        {
            h = i - 1;
            break;
        }
    }
    min_r = h * (h + 1) / 2 - g;
    for(int i = 1; i <= h; i++) 
    {
        for(int j = r; j >= 0; j--)  
        {
            if(j - i >= 0)
                dp[j] = (dp[j] % MOD + dp[j - i] % MOD) % MOD;
            if(i == h && j >= min_r) 
                ans = (ans % MOD + dp[j] % MOD) % MOD;
        }
    }
    printf("%d
", ans);
}

版权声明：本文博主原创文章，博客，未经同意不得转载。