PAT.1053 Path of Equal Weight(dfs, died)

1053 Path of Equal Weight (30分)

 

Given a non-empty tree with root R, and with weight W​i​​ assigned to each tree node T​i​​. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.

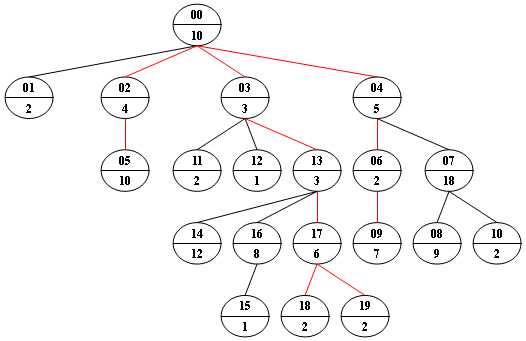
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let's consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0, the number of nodes in a tree, M (<), the number of non-leaf nodes, and 0, the given weight number. The next line contains N positive numbers where W​i​​ (<) corresponds to the tree node T​i​​. Then M lines follow, each in the format:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 00.

Output Specification:

For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.

Note: sequence { is said to be greater than sequence { if there exists 1 such that A​i​​=B​i​​ for ,, and A​k+1​​>B​k+1​​.

Sample Input:

20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19

Sample Output:

10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2



行吧，又是一道想杀死自己的题目。
这题，一上来愣头青写了一发，结果第一个样例死活wrong。吐了。
原因呢？是因为没有认真审题(其实就是菜)，题目要求路径起点必须是root，重点必须是leaf node.....
行吧，我知道自己菜了。微笑脸.jpg

顺便强烈推荐一下这题我的写法，我存图用的是链式前向星，这个数据结构是真的好用，干啥都好，有需要的兄弟可以
传送门走一波/xyx

哦，对了，还记录一个小插曲。
如下
我那未编辑完且未发送的自信和躁动...还专门找了个算法笔记的pdf去看了看，结果人家一上来就告诉我我错哪了....

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;

const int maxn = 100 + 5;

int weight[maxn];

int n, m, s;

struct Edge {
    int to, next;
} edges[maxn * maxn];

int head[maxn], cnt;

void init() {
    memset(head, -1, sizeof head);
    cnt = 2;
}

void addedge(int u, int v) {
    edges[cnt].to = v; edges[cnt].next= head[u];
    head[u] = cnt ++;
}

vector <int> path;
vector <int> ans[maxn];

int tot, tot_path;


void dfs(int u) {
    if(tot == s && !~head[u]) {
        ans[tot_path ++] = path;
        return;
    } else if(tot > s) {
        return;
    }
    for(int k = head[u]; ~k; k = edges[k].next) {
        int v = edges[k].to;
        tot += weight[v];
        path.push_back(weight[v]);
        dfs(v);
        tot -= weight[v];
        path.pop_back();
    }
}

bool cmp(vector <int> a, vector <int> b) {
    for(int i = 0; i < min(a.size(), b.size()); i ++) {
        if(a[i] != b[i]) return a[i] > b[i];
    }
    return a.size() > b.size();
}

int main() {
    init();
    scanf("%d %d %d", &n, &m, &s);
    for(int i = 0; i < n; i ++) {
        scanf("%d", &weight[i]);
    }
    int u, v, num;
    while(m --) {
        scanf("%d %d", &u, &num);
        while(num --) {
            scanf("%d", &v);
            addedge(u, v);
        }
    }
    for(int i = 0; i < 1; i ++) {
        path.clear();
        tot = weight[i];
        path.push_back(weight[i]);
        dfs(i);
    }
    sort(ans, ans + tot_path, cmp);
    for(int i = 0; i < tot_path; i ++) {
        for(int j = 0; j < ans[i].size(); j ++) {
            if(j) printf(" ");
            printf("%d", ans[i][j]);
        }
        printf("
");
    }
    return 0;
}