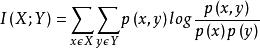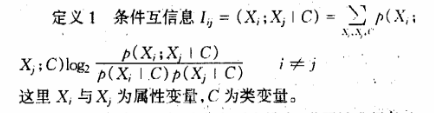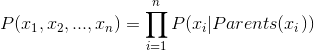前言
在前面的时间里已经学习过了NB朴素贝叶斯算法, 又刚刚初步的学习了贝叶斯网络的一些基本概念和常用的计算方法。于是就有了上篇初识贝叶斯网络的文章,由于本人最近一直在研究学习<<贝叶斯网引论>>,也接触到了许多与贝叶斯网络相关的知识,可以说朴素贝叶斯算法这些只是我们所了解贝叶斯知识的很小的一部分。今天我要总结的学习成果就是基于NB算法的,叫做Tree Augmented Naive Bays,中文意思就是树型朴素贝叶斯算法,简单理解就是树增强型NB算法,那么问题来了,他是如何增强的呢,请继续往下正文的描述。
朴素贝叶斯算法
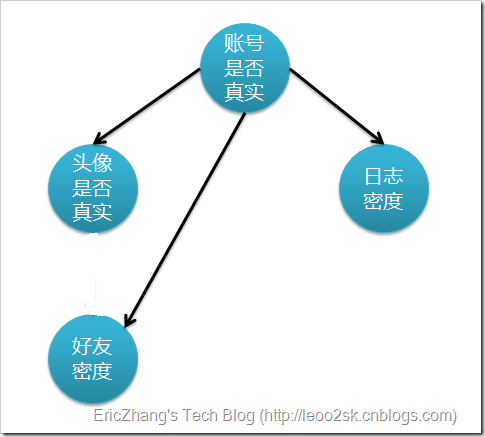
又得要从朴素贝叶斯算法开始讲起了,因为在前言中已经说了,TAN算法是对NB算法的增强,了解过NB算法的,一定知道NB算法在使用的时候是假设属性事件是相互独立的,而决策属性的分类结果是依赖于各个条件属性的情况的,最后选择分类属性中拥有最大后验概率的值为决策属性。比如下面这个模型可以描述一个简单的模型,
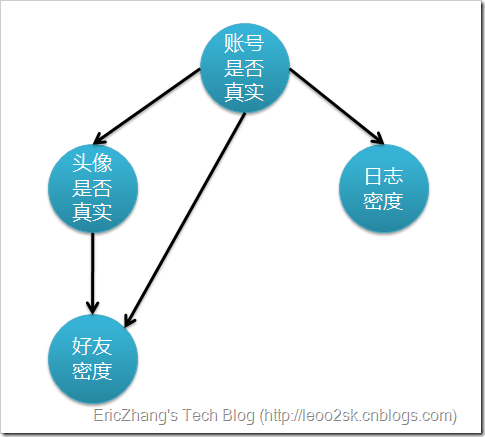
上面账号是否真实的依赖属性条件有3个,好友密度,是否使用真实头像,日志密度,假设这3个属性是相互独立的,但是事实上,在这里的头像是否真实和好友密度其实是有关联的,所以更加真实的情况是下面这张情况;
OK,TAN的出现就解决了条件间的部分属性依赖的问题。在上面的例子中我们是根据自己的主观意识判断出头像和好友密度的关系,但是在真实算法中,我们当然希望机器能够自己根据所给数据集帮我们得出这样的关系,令人高兴的事,TAN帮我们做到了这点。
TAN算法
互信息值
互信息值,在百度百科中的解释如下:
互信息值是信息论中一个有用的信息度量。它可以看出是一个信息量里包含另一个随机变量的信息量。
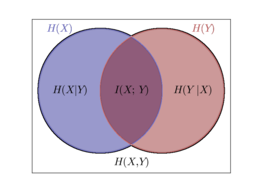
用图线来表示就是下面这样。
中间的I(x;y)就是互信息值,X,Y代表的2种属性。于是下面这个属性就很好理解了,互信息值越大,就代表2个属性关联性越大。互信息值的标准公式如下:
但是在TAN中会有少许的不一样,会有类变量属性的加入,因为属性之间的关联性的前提是要在某一分类属性确定下进行重新计算,不同的类属性值会有不同的属性关联性。下面是TAN中的I(x;Y)计算公式:
现在看不懂不要紧,后面在给出的程序代码中可自行调试。
算法实现过程
TAN的算法过程其实并不简单,在计算完各个属性对的互信息值之后,要进行贝叶斯网络的构建,这个是TAN中最难的部分,这个部分有下面几个阶段。
1、根据各个属性对的互信息值降序排序,依次取出其中的节点对,遵循不产生环路的原则,构造最大权重跨度树,直到选择完n-1条边为止(因为总共n个属性节点,n-1条边即可确定)。按照互信息值从高到低选择的原因就是要保留关联性更高的关联依赖性的边。
2、上述过程构成的是一个无向图,接下来为整个无向图确定边的方向。选择任意一个属性节点作为根节点,由根节点向外的方向为属性节点之间的方向。
3、为每一个属性节点添加父节点,父节点就是分类属性节点,至此贝叶斯网络结构构造完毕。
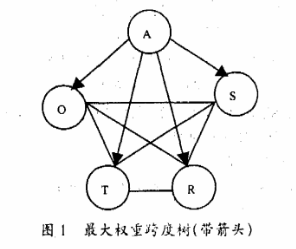
为了方便大家理解,我在网上截了几张图,下面这张是在5个属性节点中优先选择了互信息值最大的4条作为无向图:
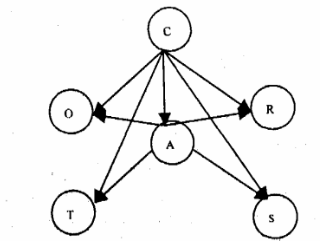
上述带了箭头是因为,我选择的A作为树的根节点,然后方向就全部确定了,因为A直接连着4个属性节点,然后再此基础上添加父节点,就是下面这个样子了。
OK,这样应该就比较好理解了吧,如果还不理解,请仔细分析我写的程序,从代码中去理解这个过程也可以。
分类结果概率的计算
分类结果概率的计算其实非常简单,只要把查询的条件属性传入分类模型中,然后计算不同类属性下的概率值,拥有最大概率值的分类属性值为最终的分类结果。下面是计算公式,就是联合概率分布公式:
代码实现
测试数据集input.txt:
OutLook Temperature Humidity Wind PlayTennis
Sunny Hot High Weak No
Sunny Hot High Strong No
Overcast Hot High Weak Yes
Rainy Mild High Weak Yes
Rainy Cool Normal Weak Yes
Rainy Cool Normal Strong No
Overcast Cool Normal Strong Yes
Sunny Mild High Weak No
Sunny Cool Normal Weak Yes
Rainy Mild Normal Weak Yes
Sunny Mild Normal Strong Yes
Overcast Mild High Strong Yes
Overcast Hot Normal Weak Yes
Rainy Mild High Strong No
package DataMining_TAN;
import java.util.ArrayList;
/**
* 贝叶斯网络节点类
*
* @author lyq
*
*/
public class Node {
//节点唯一id,方便后面节点连接方向的确定
int id;
// 节点的属性名称
String name;
// 该节点所连续的节点
ArrayList<Node> connectedNodes;
public Node(int id, String name) {
this.id = id;
this.name = name;
// 初始化变量
this.connectedNodes = new ArrayList<>();
}
/**
* 将自身节点连接到目标给定的节点
*
* @param node
* 下游节点
*/
public void connectNode(Node node) {
//避免连接自身
if(this.id == node.id){
return;
}
// 将节点加入自身节点的节点列表中
this.connectedNodes.add(node);
// 将自身节点加入到目标节点的列表中
node.connectedNodes.add(this);
}
/**
* 判断与目标节点是否相同,主要比较名称是否相同即可
*
* @param node
* 目标结点
* @return
*/
public boolean isEqual(Node node) {
boolean isEqual;
isEqual = false;
// 节点名称相同则视为相等
if (this.id == node.id) {
isEqual = true;
}
return isEqual;
}
}互信息值类.java:
package DataMining_TAN;
/**
* 属性之间的互信息值,表示属性之间的关联性大小
* @author lyq
*
*/
public class AttrMutualInfo implements Comparable<AttrMutualInfo>{
//互信息值
Double value;
//关联属性值对
Node[] nodeArray;
public AttrMutualInfo(double value, Node node1, Node node2){
this.value = value;
this.nodeArray = new Node[2];
this.nodeArray[0] = node1;
this.nodeArray[1] = node2;
}
@Override
public int compareTo(AttrMutualInfo o) {
// TODO Auto-generated method stub
return o.value.compareTo(this.value);
}
}算法主程序类TANTool.java:
package DataMining_TAN;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
/**
* TAN树型朴素贝叶斯算法工具类
*
* @author lyq
*
*/
public class TANTool {
// 测试数据集地址
private String filePath;
// 数据集属性总数,其中一个个分类属性
private int attrNum;
// 分类属性名
private String classAttrName;
// 属性列名称行
private String[] attrNames;
// 贝叶斯网络边的方向,数组内的数值为节点id,从i->j
private int[][] edges;
// 属性名到列下标的映射
private HashMap<String, Integer> attr2Column;
// 属性,属性对取值集合映射对
private HashMap<String, ArrayList<String>> attr2Values;
// 贝叶斯网络总节点列表
private ArrayList<Node> totalNodes;
// 总的测试数据
private ArrayList<String[]> totalDatas;
public TANTool(String filePath) {
this.filePath = filePath;
readDataFile();
}
/**
* 从文件中读取数据
*/
private void readDataFile() {
File file = new File(filePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] array;
while ((str = in.readLine()) != null) {
array = str.split(" ");
dataArray.add(array);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
this.totalDatas = dataArray;
this.attrNames = this.totalDatas.get(0);
this.attrNum = this.attrNames.length;
this.classAttrName = this.attrNames[attrNum - 1];
Node node;
this.edges = new int[attrNum][attrNum];
this.totalNodes = new ArrayList<>();
this.attr2Column = new HashMap<>();
this.attr2Values = new HashMap<>();
// 分类属性节点id最小设为0
node = new Node(0, attrNames[attrNum - 1]);
this.totalNodes.add(node);
for (int i = 0; i < attrNames.length; i++) {
if (i < attrNum - 1) {
// 创建贝叶斯网络节点,每个属性一个节点
node = new Node(i + 1, attrNames[i]);
this.totalNodes.add(node);
}
// 添加属性到列下标的映射
this.attr2Column.put(attrNames[i], i);
}
String[] temp;
ArrayList<String> values;
// 进行属性名,属性值对的映射匹配
for (int i = 1; i < this.totalDatas.size(); i++) {
temp = this.totalDatas.get(i);
for (int j = 0; j < temp.length; j++) {
// 判断map中是否包含此属性名
if (this.attr2Values.containsKey(attrNames[j])) {
values = this.attr2Values.get(attrNames[j]);
} else {
values = new ArrayList<>();
}
if (!values.contains(temp[j])) {
// 加入新的属性值
values.add(temp[j]);
}
this.attr2Values.put(attrNames[j], values);
}
}
}
/**
* 根据条件互信息度对构建最大权重跨度树,返回第一个节点为根节点
*
* @param iArray
*/
private Node constructWeightTree(ArrayList<Node[]> iArray) {
Node node1;
Node node2;
Node root;
ArrayList<Node> existNodes;
existNodes = new ArrayList<>();
for (Node[] i : iArray) {
node1 = i[0];
node2 = i[1];
// 将2个节点进行连接
node1.connectNode(node2);
// 避免出现环路现象
addIfNotExist(node1, existNodes);
addIfNotExist(node2, existNodes);
if (existNodes.size() == attrNum - 1) {
break;
}
}
// 返回第一个作为根节点
root = existNodes.get(0);
return root;
}
/**
* 为树型结构确定边的方向,方向为属性根节点方向指向其他属性节点方向
*
* @param root
* 当前遍历到的节点
*/
private void confirmGraphDirection(Node currentNode) {
int i;
int j;
ArrayList<Node> connectedNodes;
connectedNodes = currentNode.connectedNodes;
i = currentNode.id;
for (Node n : connectedNodes) {
j = n.id;
// 判断连接此2节点的方向是否被确定
if (edges[i][j] == 0 && edges[j][i] == 0) {
// 如果没有确定,则制定方向为i->j
edges[i][j] = 1;
// 递归继续搜索
confirmGraphDirection(n);
}
}
}
/**
* 为属性节点添加分类属性节点为父节点
*
* @param parentNode
* 父节点
* @param nodeList
* 子节点列表
*/
private void addParentNode() {
// 分类属性节点
Node parentNode;
parentNode = null;
for (Node n : this.totalNodes) {
if (n.id == 0) {
parentNode = n;
break;
}
}
for (Node child : this.totalNodes) {
parentNode.connectNode(child);
if (child.id != 0) {
// 确定连接方向
this.edges[0][child.id] = 1;
}
}
}
/**
* 在节点集合中添加节点
*
* @param node
* 待添加节点
* @param existNodes
* 已存在的节点列表
* @return
*/
public boolean addIfNotExist(Node node, ArrayList<Node> existNodes) {
boolean canAdd;
canAdd = true;
for (Node n : existNodes) {
// 如果节点列表中已经含有节点,则算添加失败
if (n.isEqual(node)) {
canAdd = false;
break;
}
}
if (canAdd) {
existNodes.add(node);
}
return canAdd;
}
/**
* 计算节点条件概率
*
* @param node
* 关于node的后验概率
* @param queryParam
* 查询的属性参数
* @return
*/
private double calConditionPro(Node node, HashMap<String, String> queryParam) {
int id;
double pro;
String value;
String[] attrValue;
ArrayList<String[]> priorAttrInfos;
ArrayList<String[]> backAttrInfos;
ArrayList<Node> parentNodes;
pro = 1;
id = node.id;
parentNodes = new ArrayList<>();
priorAttrInfos = new ArrayList<>();
backAttrInfos = new ArrayList<>();
for (int i = 0; i < this.edges.length; i++) {
// 寻找父节点id
if (this.edges[i][id] == 1) {
for (Node temp : this.totalNodes) {
// 寻找目标节点id
if (temp.id == i) {
parentNodes.add(temp);
break;
}
}
}
}
// 获取先验属性的属性值,首先添加先验属性
value = queryParam.get(node.name);
attrValue = new String[2];
attrValue[0] = node.name;
attrValue[1] = value;
priorAttrInfos.add(attrValue);
// 逐一添加后验属性
for (Node p : parentNodes) {
value = queryParam.get(p.name);
attrValue = new String[2];
attrValue[0] = p.name;
attrValue[1] = value;
backAttrInfos.add(attrValue);
}
pro = queryConditionPro(priorAttrInfos, backAttrInfos);
return pro;
}
/**
* 查询条件概率
*
* @param attrValues
* 条件属性值
* @return
*/
private double queryConditionPro(ArrayList<String[]> priorValues,
ArrayList<String[]> backValues) {
// 判断是否满足先验属性值条件
boolean hasPrior;
// 判断是否满足后验属性值条件
boolean hasBack;
int attrIndex;
double backPro;
double totalPro;
double pro;
String[] tempData;
pro = 0;
totalPro = 0;
backPro = 0;
// 跳过第一行的属性名称行
for (int i = 1; i < this.totalDatas.size(); i++) {
tempData = this.totalDatas.get(i);
hasPrior = true;
hasBack = true;
// 判断是否满足先验条件
for (String[] array : priorValues) {
attrIndex = this.attr2Column.get(array[0]);
// 判断值是否满足条件
if (!tempData[attrIndex].equals(array[1])) {
hasPrior = false;
break;
}
}
// 判断是否满足后验条件
for (String[] array : backValues) {
attrIndex = this.attr2Column.get(array[0]);
// 判断值是否满足条件
if (!tempData[attrIndex].equals(array[1])) {
hasBack = false;
break;
}
}
// 进行计数统计,分别计算满足后验属性的值和同时满足条件的个数
if (hasBack) {
backPro++;
if (hasPrior) {
totalPro++;
}
} else if (hasPrior && backValues.size() == 0) {
// 如果只有先验概率则为纯概率的计算
totalPro++;
backPro = 1.0;
}
}
if (backPro == 0) {
pro = 0;
} else {
// 计算总的概率=都发生概率/只发生后验条件的时间概率
pro = totalPro / backPro;
}
return pro;
}
/**
* 输入查询条件参数,计算发生概率
*
* @param queryParam
* 条件参数
* @return
*/
public double calHappenedPro(String queryParam) {
double result;
double temp;
// 分类属性值
String classAttrValue;
String[] array;
String[] array2;
HashMap<String, String> params;
result = 1;
params = new HashMap<>();
// 进行查询字符的参数分解
array = queryParam.split(",");
for (String s : array) {
array2 = s.split("=");
params.put(array2[0], array2[1]);
}
classAttrValue = params.get(classAttrName);
// 构建贝叶斯网络结构
constructBayesNetWork(classAttrValue);
for (Node n : this.totalNodes) {
temp = calConditionPro(n, params);
// 为了避免出现条件概率为0的现象,进行轻微矫正
if (temp == 0) {
temp = 0.001;
}
// 按照联合概率公式,进行乘积运算
result *= temp;
}
return result;
}
/**
* 构建树型贝叶斯网络结构
*
* @param value
* 类别量值
*/
private void constructBayesNetWork(String value) {
Node rootNode;
ArrayList<AttrMutualInfo> mInfoArray;
// 互信息度对
ArrayList<Node[]> iArray;
iArray = null;
rootNode = null;
// 在每次重新构建贝叶斯网络结构的时候,清空原有的连接结构
for (Node n : this.totalNodes) {
n.connectedNodes.clear();
}
this.edges = new int[attrNum][attrNum];
// 从互信息对象中取出属性值对
iArray = new ArrayList<>();
mInfoArray = calAttrMutualInfoArray(value);
for (AttrMutualInfo v : mInfoArray) {
iArray.add(v.nodeArray);
}
// 构建最大权重跨度树
rootNode = constructWeightTree(iArray);
// 为无向图确定边的方向
confirmGraphDirection(rootNode);
// 为每个属性节点添加分类属性父节点
addParentNode();
}
/**
* 给定分类变量值,计算属性之间的互信息值
*
* @param value
* 分类变量值
* @return
*/
private ArrayList<AttrMutualInfo> calAttrMutualInfoArray(String value) {
double iValue;
Node node1;
Node node2;
AttrMutualInfo mInfo;
ArrayList<AttrMutualInfo> mInfoArray;
mInfoArray = new ArrayList<>();
for (int i = 0; i < this.totalNodes.size() - 1; i++) {
node1 = this.totalNodes.get(i);
// 跳过分类属性节点
if (node1.id == 0) {
continue;
}
for (int j = i + 1; j < this.totalNodes.size(); j++) {
node2 = this.totalNodes.get(j);
// 跳过分类属性节点
if (node2.id == 0) {
continue;
}
// 计算2个属性节点之间的互信息值
iValue = calMutualInfoValue(node1, node2, value);
mInfo = new AttrMutualInfo(iValue, node1, node2);
mInfoArray.add(mInfo);
}
}
// 将结果进行降序排列,让互信息值高的优先用于构建树
Collections.sort(mInfoArray);
return mInfoArray;
}
/**
* 计算2个属性节点的互信息值
*
* @param node1
* 节点1
* @param node2
* 节点2
* @param vlaue
* 分类变量值
*/
private double calMutualInfoValue(Node node1, Node node2, String value) {
double iValue;
double temp;
// 三种不同条件的后验概率
double pXiXj;
double pXi;
double pXj;
String[] array1;
String[] array2;
ArrayList<String> attrValues1;
ArrayList<String> attrValues2;
ArrayList<String[]> priorValues;
// 后验概率,在这里就是类变量值
ArrayList<String[]> backValues;
array1 = new String[2];
array2 = new String[2];
priorValues = new ArrayList<>();
backValues = new ArrayList<>();
iValue = 0;
array1[0] = classAttrName;
array1[1] = value;
// 后验属性都是类属性
backValues.add(array1);
// 获取节点属性的属性值集合
attrValues1 = this.attr2Values.get(node1.name);
attrValues2 = this.attr2Values.get(node2.name);
for (String v1 : attrValues1) {
for (String v2 : attrValues2) {
priorValues.clear();
array1 = new String[2];
array1[0] = node1.name;
array1[1] = v1;
priorValues.add(array1);
array2 = new String[2];
array2[0] = node2.name;
array2[1] = v2;
priorValues.add(array2);
// 计算3种条件下的概率
pXiXj = queryConditionPro(priorValues, backValues);
priorValues.clear();
priorValues.add(array1);
pXi = queryConditionPro(priorValues, backValues);
priorValues.clear();
priorValues.add(array2);
pXj = queryConditionPro(priorValues, backValues);
// 如果出现其中一个计数概率为0,则直接赋值为0处理
if (pXiXj == 0 || pXi == 0 || pXj == 0) {
temp = 0;
} else {
// 利用公式计算针对此属性值对组合的概率
temp = pXiXj * Math.log(pXiXj / (pXi * pXj)) / Math.log(2);
}
// 进行和属性值对组合的累加即为整个属性的互信息值
iValue += temp;
}
}
return iValue;
}
}
package DataMining_TAN;
/**
* TAN树型朴素贝叶斯算法
*
* @author lyq
*
*/
public class Client {
public static void main(String[] args) {
String filePath = "C:\Users\lyq\Desktop\icon\input.txt";
// 条件查询语句
String queryStr;
// 分类结果概率1
double classResult1;
// 分类结果概率2
double classResult2;
TANTool tool = new TANTool(filePath);
queryStr = "OutLook=Sunny,Temperature=Hot,Humidity=High,Wind=Weak,PlayTennis=No";
classResult1 = tool.calHappenedPro(queryStr);
queryStr = "OutLook=Sunny,Temperature=Hot,Humidity=High,Wind=Weak,PlayTennis=Yes";
classResult2 = tool.calHappenedPro(queryStr);
System.out.println(String.format("类别为%s所求得的概率为%s", "PlayTennis=No",
classResult1));
System.out.println(String.format("类别为%s所求得的概率为%s", "PlayTennis=Yes",
classResult2));
if (classResult1 > classResult2) {
System.out.println("分类类别为PlayTennis=No");
} else {
System.out.println("分类类别为PlayTennis=Yes");
}
}
}类别为PlayTennis=No所求得的概率为0.09523809523809525
类别为PlayTennis=Yes所求得的概率为3.571428571428571E-5
分类类别为PlayTennis=No
参考文献
百度百科
贝叶斯网络分类器与应用,作者:余民杰
用于数据挖掘的TAN分类器的研究和应用,作者:孙笑徽等4人
更多数据挖掘算法
https://github.com/linyiqun/DataMiningAlgorithm