CART分类回归树算法
与上次文章中提到的ID3算法和C4.5算法类似,CART算法也是一种决策树分类算法。CART分类回归树算法的本质也是对数据进行分类的,最终数据的表现形式也是以树形的模式展现的,与ID3,C4.5算法不同的是,他的分类标准所采用的算法不同了。下面列出了其中的一些不同之处:
1、CART最后形成的树是一个二叉树,每个节点会分成2个节点,左孩子节点和右孩子节点,而在ID3和C4.5中是按照分类属性的值类型进行划分,于是这就要求CART算法在所选定的属性中又要划分出最佳的属性划分值,节点如果选定了划分属性名称还要确定里面按照那个值做一个二元的划分。
2、CART算法对于属性的值采用的是基于Gini系数值的方式做比较,gini某个属性的某次值的划分的gini指数的值为:

比如体温为恒温时包含哺乳类5个、鸟类2个,则:
体温为非恒温时包含爬行类3个、鱼类3个、两栖类2个,则
所以如果按照“体温为恒温和非恒温”进行划分的话,我们得到GINI的增益(类比信息增益):
最好的划分就是使得GINI_Gain最小的划分。
通过比较每个属性的最小的gini指数值,作为最后的结果。3、CART算法在把数据进行分类之后,会对树进行一个剪枝,常用的用前剪枝和后剪枝法,而常见的后剪枝发包括代价复杂度剪枝,悲观误差剪枝等等,我写的此次算法采用的是代价复杂度剪枝法。代价复杂度剪枝的算法公式为:
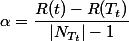
里面变量的意思为:
是子树中包含的叶子节点个数;
是节点t的误差代价,如果该节点被剪枝;
r(t)是节点t的误差率;
p(t)是节点t上的数据占所有数据的比例。
是子树Tt的误差代价,如果该节点不被剪枝。它等于子树Tt上所有叶子节点的误差代价之和。下面说说我对于这个公式的理解:其实这个公式的本质是对于剪枝前和剪枝后的样本偏差率做一个差值比较,一个好的分类当然是分类后的样本偏差率相较于没分类(就是剪枝掉的时候)的偏差率小,所以这时的值就会大,如果分类前后基本变化不大,则意味着分类不起什么效果,α值的分子位置就小,所以误差代价就小,可以被剪枝。但是一般分类后的偏差率会小于分类前的,因为偏差数在高层节点的时候肯定比子节点的多,子节点偏差数最多与父亲节点一样。
CART算法实现
首先是程序的备用数据,我是把他存在了一个文字中,通过程序进行逐行的读取:
Rid Age Income Student CreditRating BuysComputer
1 Youth High No Fair No
2 Youth High No Excellent No
3 MiddleAged High No Fair Yes
4 Senior Medium No Fair Yes
5 Senior Low Yes Fair Yes
6 Senior Low Yes Excellent No
7 MiddleAged Low Yes Excellent Yes
8 Youth Medium No Fair No
9 Youth Low Yes Fair Yes
10 Senior Medium Yes Fair Yes
11 Youth Medium Yes Excellent Yes
12 MiddleAged Medium No Excellent Yes
13 MiddleAged High Yes Fair Yes
14 Senior Medium No Excellent No
package DataMing_CART;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Map;
import java.util.Queue;
import javax.lang.model.element.NestingKind;
import javax.swing.text.DefaultEditorKit.CutAction;
import javax.swing.text.html.MinimalHTMLWriter;
/**
* CART分类回归树算法工具类
*
* @author lyq
*
*/
public class CARTTool {
// 类标号的值类型
private final String YES = "Yes";
private final String NO = "No";
// 所有属性的类型总数,在这里就是data源数据的列数
private int attrNum;
private String filePath;
// 初始源数据,用一个二维字符数组存放模仿表格数据
private String[][] data;
// 数据的属性行的名字
private String[] attrNames;
// 每个属性的值所有类型
private HashMap<String, ArrayList<String>> attrValue;
public CARTTool(String filePath) {
this.filePath = filePath;
attrValue = new HashMap<>();
}
/**
* 从文件中读取数据
*/
public void readDataFile() {
File file = new File(filePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
data = new String[dataArray.size()][];
dataArray.toArray(data);
attrNum = data[0].length;
attrNames = data[0];
/*
* for (int i = 0; i < data.length; i++) { for (int j = 0; j <
* data[0].length; j++) { System.out.print(" " + data[i][j]); }
* System.out.print("
"); }
*/
}
/**
* 首先初始化每种属性的值的所有类型,用于后面的子类熵的计算时用
*/
public void initAttrValue() {
ArrayList<String> tempValues;
// 按照列的方式,从左往右找
for (int j = 1; j < attrNum; j++) {
// 从一列中的上往下开始寻找值
tempValues = new ArrayList<>();
for (int i = 1; i < data.length; i++) {
if (!tempValues.contains(data[i][j])) {
// 如果这个属性的值没有添加过,则添加
tempValues.add(data[i][j]);
}
}
// 一列属性的值已经遍历完毕,复制到map属性表中
attrValue.put(data[0][j], tempValues);
}
/*
* for (Map.Entry entry : attrValue.entrySet()) {
* System.out.println("key:value " + entry.getKey() + ":" +
* entry.getValue()); }
*/
}
/**
* 计算机基尼指数
*
* @param remainData
* 剩余数据
* @param attrName
* 属性名称
* @param value
* 属性值
* @param beLongValue
* 分类是否属于此属性值
* @return
*/
public double computeGini(String[][] remainData, String attrName,
String value, boolean beLongValue) {
// 实例总数
int total = 0;
// 正实例数
int posNum = 0;
// 负实例数
int negNum = 0;
// 基尼指数
double gini = 0;
// 还是按列从左往右遍历属性
for (int j = 1; j < attrNames.length; j++) {
// 找到了指定的属性
if (attrName.equals(attrNames[j])) {
for (int i = 1; i < remainData.length; i++) {
// 统计正负实例按照属于和不属于值类型进行划分
if ((beLongValue && remainData[i][j].equals(value))
|| (!beLongValue && !remainData[i][j].equals(value))) {
if (remainData[i][attrNames.length - 1].equals(YES)) {
// 判断此行数据是否为正实例
posNum++;
} else {
negNum++;
}
}
}
}
}
total = posNum + negNum;
double posProbobly = (double) posNum / total;
double negProbobly = (double) negNum / total;
gini = 1 - posProbobly * posProbobly - negProbobly * negProbobly;
// 返回计算基尼指数
return gini;
}
/**
* 计算属性划分的最小基尼指数,返回最小的属性值划分和最小的基尼指数,保存在一个数组中
*
* @param remainData
* 剩余谁
* @param attrName
* 属性名称
* @return
*/
public String[] computeAttrGini(String[][] remainData, String attrName) {
String[] str = new String[2];
// 最终该属性的划分类型值
String spiltValue = "";
// 临时变量
int tempNum = 0;
// 保存属性的值划分时的最小的基尼指数
double minGini = Integer.MAX_VALUE;
ArrayList<String> valueTypes = attrValue.get(attrName);
// 属于此属性值的实例数
HashMap<String, Integer> belongNum = new HashMap<>();
for (String string : valueTypes) {
// 重新计数的时候,数字归0
tempNum = 0;
// 按列从左往右遍历属性
for (int j = 1; j < attrNames.length; j++) {
// 找到了指定的属性
if (attrName.equals(attrNames[j])) {
for (int i = 1; i < remainData.length; i++) {
// 统计正负实例按照属于和不属于值类型进行划分
if (remainData[i][j].equals(string)) {
tempNum++;
}
}
}
}
belongNum.put(string, tempNum);
}
double tempGini = 0;
double posProbably = 1.0;
double negProbably = 1.0;
for (String string : valueTypes) {
tempGini = 0;
posProbably = 1.0 * belongNum.get(string) / (remainData.length - 1);
negProbably = 1 - posProbably;
tempGini += posProbably
* computeGini(remainData, attrName, string, true);
tempGini += negProbably
* computeGini(remainData, attrName, string, false);
if (tempGini < minGini) {
minGini = tempGini;
spiltValue = string;
}
}
str[0] = spiltValue;
str[1] = minGini + "";
return str;
}
public void buildDecisionTree(AttrNode node, String parentAttrValue,
String[][] remainData, ArrayList<String> remainAttr,
boolean beLongParentValue) {
// 属性划分值
String valueType = "";
// 划分属性名称
String spiltAttrName = "";
double minGini = Integer.MAX_VALUE;
double tempGini = 0;
// 基尼指数数组,保存了基尼指数和此基尼指数的划分属性值
String[] giniArray;
if (beLongParentValue) {
node.setParentAttrValue(parentAttrValue);
} else {
node.setParentAttrValue("!" + parentAttrValue);
}
if (remainAttr.size() == 0) {
if (remainData.length > 1) {
ArrayList<String> indexArray = new ArrayList<>();
for (int i = 1; i < remainData.length; i++) {
indexArray.add(remainData[i][0]);
}
node.setDataIndex(indexArray);
}
System.out.println("attr remain null");
return;
}
for (String str : remainAttr) {
giniArray = computeAttrGini(remainData, str);
tempGini = Double.parseDouble(giniArray[1]);
if (tempGini < minGini) {
spiltAttrName = str;
minGini = tempGini;
valueType = giniArray[0];
}
}
// 移除划分属性
remainAttr.remove(spiltAttrName);
node.setAttrName(spiltAttrName);
// 孩子节点,分类回归树中,每次二元划分,分出2个孩子节点
AttrNode[] childNode = new AttrNode[2];
String[][] rData;
boolean[] bArray = new boolean[] { true, false };
for (int i = 0; i < bArray.length; i++) {
// 二元划分属于属性值的划分
rData = removeData(remainData, spiltAttrName, valueType, bArray[i]);
boolean sameClass = true;
ArrayList<String> indexArray = new ArrayList<>();
for (int k = 1; k < rData.length; k++) {
indexArray.add(rData[k][0]);
// 判断是否为同一类的
if (!rData[k][attrNames.length - 1]
.equals(rData[1][attrNames.length - 1])) {
// 只要有1个不相等,就不是同类型的
sameClass = false;
break;
}
}
childNode[i] = new AttrNode();
if (!sameClass) {
// 创建新的对象属性,对象的同个引用会出错
ArrayList<String> rAttr = new ArrayList<>();
for (String str : remainAttr) {
rAttr.add(str);
}
buildDecisionTree(childNode[i], valueType, rData, rAttr,
bArray[i]);
} else {
String pAtr = (bArray[i] ? valueType : "!" + valueType);
childNode[i].setParentAttrValue(pAtr);
childNode[i].setDataIndex(indexArray);
}
}
node.setChildAttrNode(childNode);
}
/**
* 属性划分完毕,进行数据的移除
*
* @param srcData
* 源数据
* @param attrName
* 划分的属性名称
* @param valueType
* 属性的值类型
* @parame beLongValue 分类是否属于此值类型
*/
private String[][] removeData(String[][] srcData, String attrName,
String valueType, boolean beLongValue) {
String[][] desDataArray;
ArrayList<String[]> desData = new ArrayList<>();
// 待删除数据
ArrayList<String[]> selectData = new ArrayList<>();
selectData.add(attrNames);
// 数组数据转化到列表中,方便移除
for (int i = 0; i < srcData.length; i++) {
desData.add(srcData[i]);
}
// 还是从左往右一列列的查找
for (int j = 1; j < attrNames.length; j++) {
if (attrNames[j].equals(attrName)) {
for (int i = 1; i < desData.size(); i++) {
if (desData.get(i)[j].equals(valueType)) {
// 如果匹配这个数据,则移除其他的数据
selectData.add(desData.get(i));
}
}
}
}
if (beLongValue) {
desDataArray = new String[selectData.size()][];
selectData.toArray(desDataArray);
} else {
// 属性名称行不移除
selectData.remove(attrNames);
// 如果是划分不属于此类型的数据时,进行移除
desData.removeAll(selectData);
desDataArray = new String[desData.size()][];
desData.toArray(desDataArray);
}
return desDataArray;
}
public void startBuildingTree() {
readDataFile();
initAttrValue();
ArrayList<String> remainAttr = new ArrayList<>();
// 添加属性,除了最后一个类标号属性
for (int i = 1; i < attrNames.length - 1; i++) {
remainAttr.add(attrNames[i]);
}
AttrNode rootNode = new AttrNode();
buildDecisionTree(rootNode, "", data, remainAttr, false);
setIndexAndAlpah(rootNode, 0, false);
System.out.println("剪枝前:");
showDecisionTree(rootNode, 1);
setIndexAndAlpah(rootNode, 0, true);
System.out.println("
剪枝后:");
showDecisionTree(rootNode, 1);
}
/**
* 显示决策树
*
* @param node
* 待显示的节点
* @param blankNum
* 行空格符,用于显示树型结构
*/
private void showDecisionTree(AttrNode node, int blankNum) {
System.out.println();
for (int i = 0; i < blankNum; i++) {
System.out.print(" ");
}
System.out.print("--");
// 显示分类的属性值
if (node.getParentAttrValue() != null
&& node.getParentAttrValue().length() > 0) {
System.out.print(node.getParentAttrValue());
} else {
System.out.print("--");
}
System.out.print("--");
if (node.getDataIndex() != null && node.getDataIndex().size() > 0) {
String i = node.getDataIndex().get(0);
System.out.print("【" + node.getNodeIndex() + "】类别:"
+ data[Integer.parseInt(i)][attrNames.length - 1]);
System.out.print("[");
for (String index : node.getDataIndex()) {
System.out.print(index + ", ");
}
System.out.print("]");
} else {
// 递归显示子节点
System.out.print("【" + node.getNodeIndex() + ":"
+ node.getAttrName() + "】");
if (node.getChildAttrNode() != null) {
for (AttrNode childNode : node.getChildAttrNode()) {
showDecisionTree(childNode, 2 * blankNum);
}
} else {
System.out.print("【 Child Null】");
}
}
}
/**
* 为节点设置序列号,并计算每个节点的误差率,用于后面剪枝
*
* @param node
* 开始的时候传入的是根节点
* @param index
* 开始的索引号,从1开始
* @param ifCutNode
* 是否需要剪枝
*/
private void setIndexAndAlpah(AttrNode node, int index, boolean ifCutNode) {
AttrNode tempNode;
// 最小误差代价节点,即将被剪枝的节点
AttrNode minAlphaNode = null;
double minAlpah = Integer.MAX_VALUE;
Queue<AttrNode> nodeQueue = new LinkedList<AttrNode>();
nodeQueue.add(node);
while (nodeQueue.size() > 0) {
index++;
// 从队列头部获取首个节点
tempNode = nodeQueue.poll();
tempNode.setNodeIndex(index);
if (tempNode.getChildAttrNode() != null) {
for (AttrNode childNode : tempNode.getChildAttrNode()) {
nodeQueue.add(childNode);
}
computeAlpha(tempNode);
if (tempNode.getAlpha() < minAlpah) {
minAlphaNode = tempNode;
minAlpah = tempNode.getAlpha();
} else if (tempNode.getAlpha() == minAlpah) {
// 如果误差代价值一样,比较包含的叶子节点个数,剪枝有多叶子节点数的节点
if (tempNode.getLeafNum() > minAlphaNode.getLeafNum()) {
minAlphaNode = tempNode;
}
}
}
}
if (ifCutNode) {
// 进行树的剪枝,让其左右孩子节点为null
minAlphaNode.setChildAttrNode(null);
}
}
/**
* 为非叶子节点计算误差代价,这里的后剪枝法用的是CCP代价复杂度剪枝
*
* @param node
* 待计算的非叶子节点
*/
private void computeAlpha(AttrNode node) {
double rt = 0;
double Rt = 0;
double alpha = 0;
// 当前节点的数据总数
int sumNum = 0;
// 最少的偏差数
int minNum = 0;
ArrayList<String> dataIndex;
ArrayList<AttrNode> leafNodes = new ArrayList<>();
addLeafNode(node, leafNodes);
node.setLeafNum(leafNodes.size());
for (AttrNode attrNode : leafNodes) {
dataIndex = attrNode.getDataIndex();
int num = 0;
sumNum += dataIndex.size();
for (String s : dataIndex) {
// 统计分类数据中的正负实例数
if (data[Integer.parseInt(s)][attrNames.length - 1].equals(YES)) {
num++;
}
}
minNum += num;
// 取小数量的值部分
if (1.0 * num / dataIndex.size() > 0.5) {
num = dataIndex.size() - num;
}
rt += (1.0 * num / (data.length - 1));
}
//同样取出少偏差的那部分
if (1.0 * minNum / sumNum > 0.5) {
minNum = sumNum - minNum;
}
Rt = 1.0 * minNum / (data.length - 1);
alpha = 1.0 * (Rt - rt) / (leafNodes.size() - 1);
node.setAlpha(alpha);
}
/**
* 筛选出节点所包含的叶子节点数
*
* @param node
* 待筛选节点
* @param leafNode
* 叶子节点列表容器
*/
private void addLeafNode(AttrNode node, ArrayList<AttrNode> leafNode) {
ArrayList<String> dataIndex;
if (node.getChildAttrNode() != null) {
for (AttrNode childNode : node.getChildAttrNode()) {
dataIndex = childNode.getDataIndex();
if (dataIndex != null && dataIndex.size() > 0) {
// 说明此节点为叶子节点
leafNode.add(childNode);
} else {
// 如果还是非叶子节点则继续递归调用
addLeafNode(childNode, leafNode);
}
}
}
}
}
/**
* 回归分类树节点
*
* @author lyq
*
*/
public class AttrNode {
// 节点属性名字
private String attrName;
// 节点索引标号
private int nodeIndex;
//包含的叶子节点数
private int leafNum;
// 节点误差率
private double alpha;
// 父亲分类属性值
private String parentAttrValue;
// 孩子节点
private AttrNode[] childAttrNode;
// 数据记录索引
private ArrayList<String> dataIndex;
.....
package DataMing_CART;
public class Client {
public static void main(String[] args){
String filePath = "C:\Users\lyq\Desktop\icon\input.txt";
CARTTool tool = new CARTTool(filePath);
tool.startBuildingTree();
}
}
剪枝前:
--!--【1:Age】
--MiddleAged--【2】类别:Yes[3, 7, 12, 13, ]
--!MiddleAged--【3:Student】
--No--【4:Income】
--High--【6】类别:No[1, 2, ]
--!High--【7:CreditRating】
--Fair--【10】类别:Yes[4, 8, ]
--!Fair--【11】类别:No[14, ]
--!No--【5:CreditRating】
--Fair--【8】类别:Yes[5, 9, 10, ]
--!Fair--【9:Income】
--Medium--【12】类别:Yes[11, ]
--!Medium--【13】类别:No[6, ]
剪枝后:
--!--【1:Age】
--MiddleAged--【2】类别:Yes[3, 7, 12, 13, ]
--!MiddleAged--【3:Student】
--No--【4:Income】【 Child Null】
--!No--【5:CreditRating】
--Fair--【8】类别:Yes[5, 9, 10, ]
--!Fair--【9:Income】
--Medium--【12】类别:Yes[11, ]
--!Medium--【13】类别:No[6, ]结果分析:
我在一开始的时候根据的是最后分类的数据是否为同一个类标识的,如果都为YES或者都为NO的,分类终止,一般情况下都说的通,但是如果最后属性划分完毕了,剩余的数据还有存在类标识不一样的情况就会偏差,比如说这里的7号CredaRating节点,下面Fair分支中的[4,8]就不是同类的。所以在后面的剪枝算法就被剪枝了。因为后面的4和7号节点的误差代价率为0,说明分类前后没有类偏差变化,这也见证了后剪枝算法的威力所在了。
在coding遇到的困难和改进的地方:
1、先说说在编码时遇到的困难,在对节点进行赋索引标号值的时候出了问题,因为是之前生成树的时候采用了DFS的思想,如果编号时也采用此方法就不对了,于是就用到了把节点取出放入队列这样的遍历方式,就是BFS的方式为节点标号。
2、程序的一个改进的地方在于算一个非叶子节点的时候需要计算他所包含的叶子节点数,采用了从当前节点开始从上往下递归计算,而且每个非叶子节点都计算一遍,显然这样做的效率是不高,后来想到了一种从叶子节点开始计算,从下往上直到根节点,对父亲节点的非叶子节点列表做更新操作,就只要计算一次,这有点dp的思想在里面了,由于时间关系,没有来得及实现。
3、第二个优化点就是后剪枝算法的多样化,我这里采用的是CCP代价复杂度算法,大家可以试着实现其他的诸如悲观误差算法进行剪枝,看看能不能把程序中4和7号节点识别出来,并且剪枝掉。
最后声明一下,用了里面的一点点的公式和例子,参考资料:http://blog.csdn.net/tianguokaka/article/details/9018933