在今天这篇博文中,博主会和大家一起探讨制作增益图的逻辑以及如何解释增益图和提升图。以下博文中,我们会运用一个直邮公司的例子来为大家讲解。假设在以往经验基础上,这家公司知道他们的直邮营销活动的平均响应率是10%。接下来我们继续假设:
* 每个邮件广告的成本 = $1
* 每个响应的返点= $50
* 发出邮件广告数量 = 10,000
基于以上假设,如果一个公司发出了10,000封邮件广告,以下表格总结了该营销活动的结果:
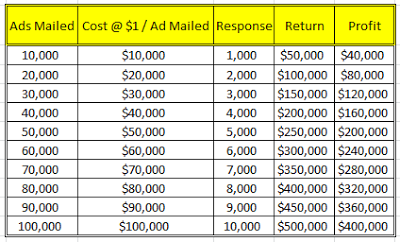
* 每个响应的返点= $50
* 发出邮件广告数量 = 10,000
基于以上假设,如果一个公司发出了10,000封邮件广告,以下表格总结了该营销活动的结果:

现在我们假设这家公司用SPSS Modeler通过历史营销数据来建预测模型。“有无响应”为目标值(target),而其他人口统计变量,社会经济变量以及行为变量为预测变量(predictors)。而该公司便可以通过预测结果来降序排列销量的期望值。因此与其向受众随机发放10,000封广告邮件,该公司可以向“最有可能响应”的10,000个客户发送邮件,然后再发放“其次可能响应”的10,000个客户发送邮件,以此类推。最终结果如下图所示:
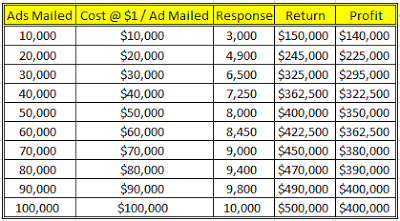
如上所示,第二个表格中的结果明显比第一个图表要更好。如果该公司对最大化收益有兴趣,利用以上的预测方法该公司便可通过花$50,000左右的成本而得到$400,000的收益,而通过第一种方法,若该公司要得到同样的收益,需要花$80,000左右的成本!
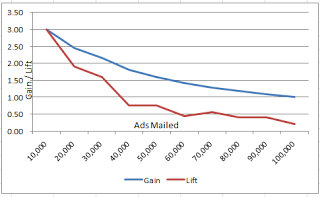
通过比较两种营销方式的响应率,我们得到了如下的结果:
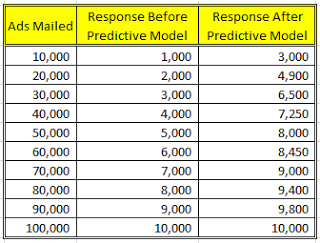
将如上数据制成折线图,我们可得到如下结果:
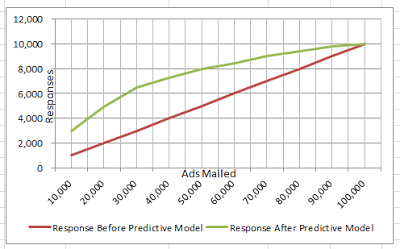
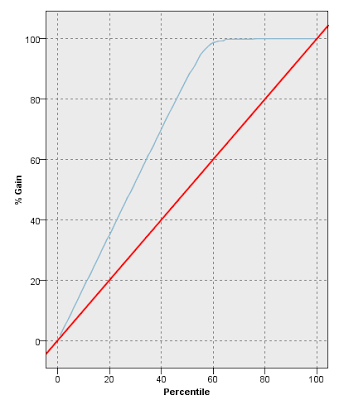
由如上图表可见,绿线(运用预测模型后的响应率)和红线(运用预测模型前的响应率)之间的差距显示了公司运用预测模型后通过降序排列销量预测值的方式来最大化利润和随机发送邮件这种方式之间的收益差距。那么,增益和提升值如何计算?我们可以通过定义这两个术语的方式来找到答案:
* 增益 = (应用预测模型的期望响应)/(随机发送的期望响应)
* 提升 = (应用预测模型的前10,000个用户的期望响应)/(随机发送的前10,000个用户的期望响应)
总结一下,增益图和提升图可以帮助解决如下的两个问题:
* 如何评估一个预测模型的好坏?
* 如何比较运用预测模型后的响应率和随机发送的响应率?Gain >1 便意味着预测模型的结果比随机发送的结果要更好。