简要题意:
求最大 (0) 矩阵。(将字符转化为数字)
本题是模板题,可以用来爆踩。???
悬线法 来了!
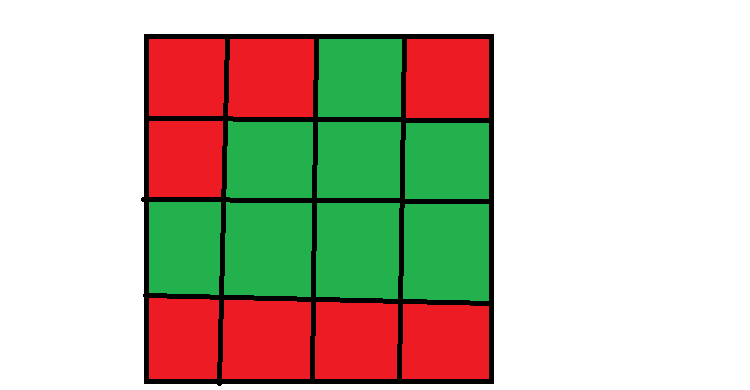
其中绿色是 (0),红色是 (1).
下面以这个图为例讲一下算法流程。
我们首先求出,以每个格子为最下面,往上堆积的最长的 (0) 条。
则所有格子的值为:
0 0 1 0
0 1 2 1
1 2 3 2
0 0 0 0
下面,对每一行,求以这一行为底的最大矩阵。
第一行:只能以 (a_{1,3}) 为底,无法往左右扩展,此时答案为 (1 imes (3-3+1) = 1).
第二行:对于 (a_{2,2}),可以往左扩展至 (2,2),往右扩展至 (2,4),此时答案为 (1 imes (4-2+1) = 3).
而 (a_{4,2}) 同理。
但 (a_{3,3}) 往上可以扩展 (1) 格,左右不得扩展,因此答案为 (2 imes (3-3+1) = 2).
所以整个第二行的答案为 (max(3,2,3) = 3).
第三行:
对于 (a_{3,1}) ,左右扩展 (4) 格,往上只有 (1) 格,答案为 (4).
对于 (a_{3,2}) ,左右扩展 (3) 格,往上只有 (2) 格,答案为 (6).
而 (a_{3,3}) ,(a_{4,4}) 同。
所以第三行的答案为 (max(4,6,6,6) = 6).
第四行没有绿格,所以答案为 (0).
综上,答案为 (max(1,3,6,0) = 6).
大家应该都懂了吧!
#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+1;
inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}
int n,m,a[N][N],h[N][N];
int l[N][N],r[N][N],ans=0;
int main(){
n=read(),m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) {
char c; cin>>c;
a[i][j]=(c=='F')?0:1;
// l[i][j]=r[i][j]=j; h[i][j]=1;
} for(int j=1;j<=m;j++) r[0][j]=m+1;
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) h[i][j]=(!a[i][j])?(h[i-1][j]+1):0; //往上扩展
int t=0;
for(int j=1;j<=m;j++)
if(!a[i][j]) l[i][j]=max(l[i-1][j],t);
else l[i][j]=0,t=j; //往左扩展
t=m+1; for(int j=m;j;j--)
if(!a[i][j]) r[i][j]=min(r[i-1][j],t);
else r[i][j]=m+1,t=j; //往右扩展
for(int j=1;j<=m;j++) ans=max(ans,(r[i][j]-l[i][j]-1)*h[i][j]);
} printf("%d
",ans*3); //别忘了*3
return 0;
}