假设检验实际上是用反证法做出非对即错的判断:先假定原假设是对的,然后将抽样数据代入相应的分布中去验证,观察原假设的数值是落在接受域还是拒绝域,由此做出是接受还是拒绝原假设的判断。
值得注意的是,不同于以往严格的数学证明,假设检验是建立在小概率事件原理的基础之上。由于小概率事件也有可能发生,因此并不能百分之百确定原假设一定不成立,也就是说,原假设也有判断错误的时候。
两种错误类型
假设检验有两种判断错误的类型,统计学家给出了专业的名称:第一类错误和第二类错误。
第一类错误(false reject):错误地拒绝,H0是对的,却拒绝了它。也就是说,计算结果落在拒绝域,但真实结果是在接受域。
第二类错误(false accept):错误地接受,H0是错的,却接受了它。也就是说,计算结果落在接受域,但真实结果是在拒绝域。
第一类错误也叫Ⅰ 型错误或弃真错误,第二类错误也叫Ⅱ 型错误或存伪错误。我觉得还是忘记这些文绉绉名称,记住false reject和false accept即可,毕竟这两个英文短语更直白,更容易理解。
假设检验的理想情况是能过做出与实际相符的正确断言,但由于抽样数据的随机性,根据样本计算的统计量必然会与整体的真实数值存在差异,这种差异可能导致出现四种判断结果:

错误的概率
既然假设检验无法保证百分之百有效,那么我们就需要研究两类错误出现的概率,由此将假设检验的功效数值化。
先来看第一类错误。
第一类错误是在H0正确的时候错误地却拒绝了它,这就意味着我们的判断结果落在了拒绝域内:
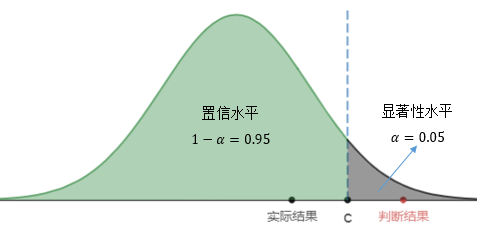
结果落在拒绝域内的概率与显著性水平一致,因此α的数值决定了出现第一类错误概率:
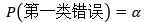
随着α的减小,第一类错误出现的概率也随之减小。当α=0时,第一类错误完全消失,也就是永远不会拒绝H0,这有点像过去的“守旧派”对于“法先王”的绝对拥护,无论时代怎么进步,“法先王”都必须服从,任何改革都视为大逆不道。
可以看出,由于α的值很小,所以犯第一类错误的几率也很小。
再来看第二类错误。
第二类错误是在H0错误的时候接受了它,一个本应落在拒绝域内的点却落在了接受域内:
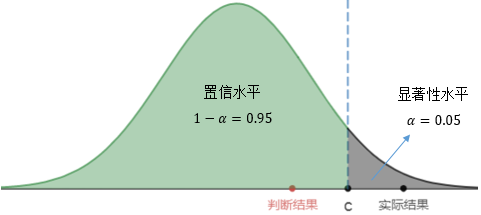
我们用β表示第二类错误出现的概率,只要α确定了,β也就确定了。一个草率的判断是β=1-α,按照这种计算方式,β=0.95,这意味着第二类错误出现的概率高达95%!如果这样,那么假设检验还有什么用?
实际上β的计算比α难得多。
我们延用产品元件的故事。μ0是改善前总体的均值,μ1是改善后总体的均值,改善前后的标准差一致,都是σ=6。
原假设H0:改善前与改善后是同一个正态分布,μ0=μ1=600。
备择假设H1:改善前与改善后是不同的正态分布,μ0 =600< μ1=603。
公司用新技术制造了大量元件,从中多次抽取容量是m(m≥30)的样本进行检验。根据中心极限定理,样本均值的分布服从均值为总体均值,方差为总体方差1/m的正态分布:
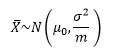
对样本均值进行标准化处理:
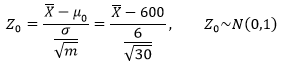
使用0.05显著性水平,在标准正态分布下,查表可知临界值是1.645。
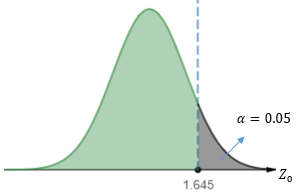
当Z0 > 1.645时,将拒绝H0假设。
再来看均值的逆运算:
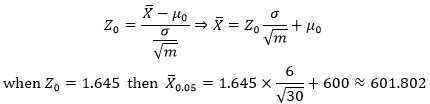
也就是说,如果抽样的均值大于601.802,就应该拒绝相信H0。

现在可以计算出标准正态分布下β区域的临界值:
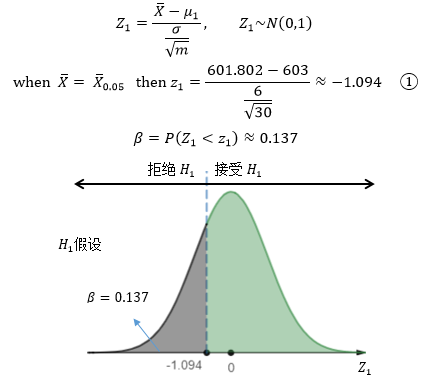
结论是,如果改善后的功率均值是603,那么以此为条件,犯第二类错误的概率是β=0.137。通过β的计算过程可以看出,只有当H1假设是一个固定的值时,才能计算出β。如果H1假设不是固定,比如只给出了μ1 > 603,那么将无法根据①计算出z1,也就无法进一步求得β。
一个常见的问题是,既然一开始就知道了H0和H1的均值和方差,为什么还要使用标准化处理?直接计算临界值岂不是更简单?
我们的确可以直接通过计算机解求得X~(μ0, σ2)时的临界值,但这是总体分布下的临界值,而我们的假设检验是基于抽样,并非总体,此时用到的理论是中心极限定理,因此才大费周章地使用标准化形态。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”
