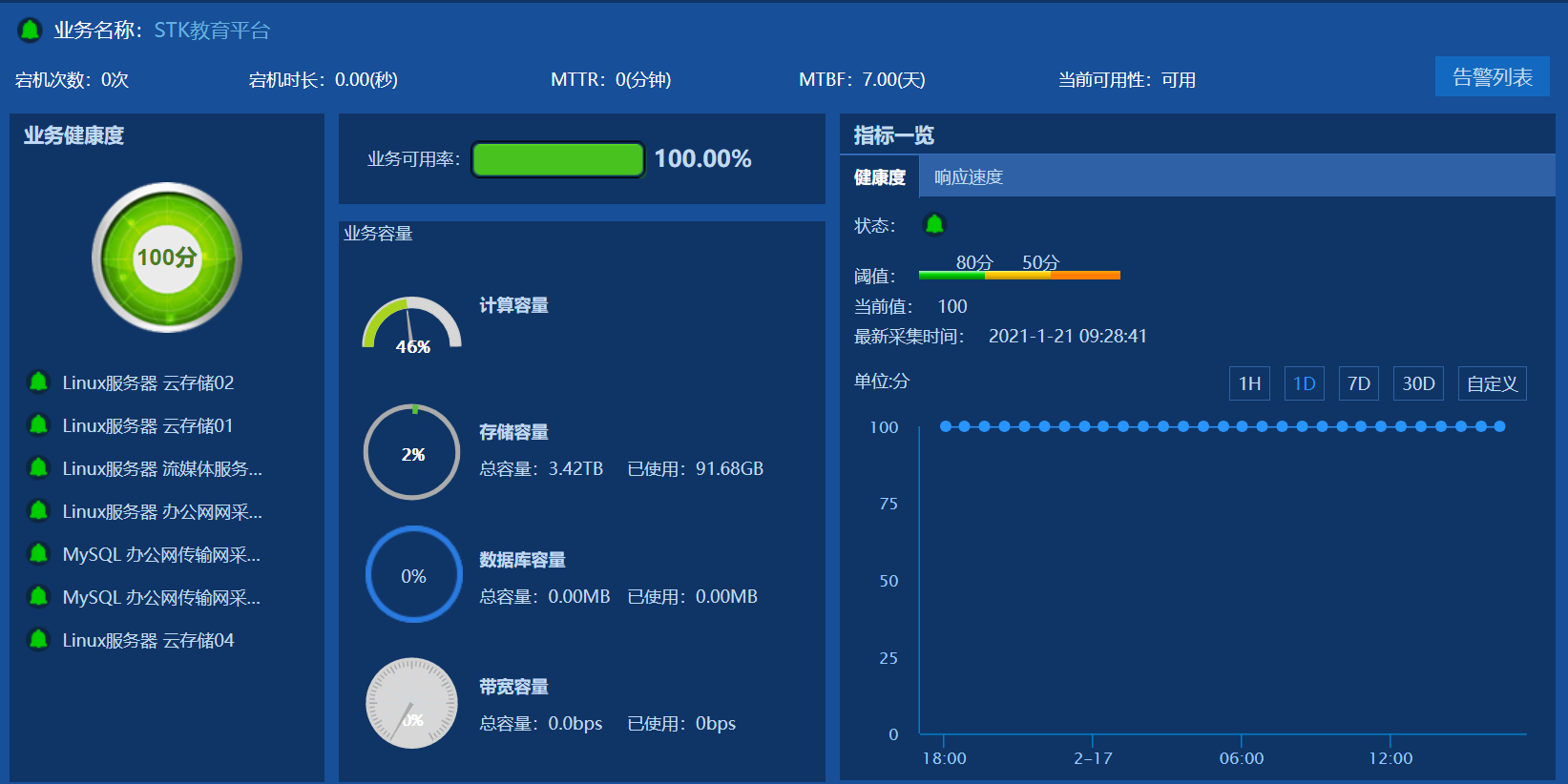
不久前,我们遇到了这样的需求:项目方需要对各个业务系统进行监控,如果业务系统的分值低于某个预定的分数,则监控系统会自动为相关负责人发送告警信息。
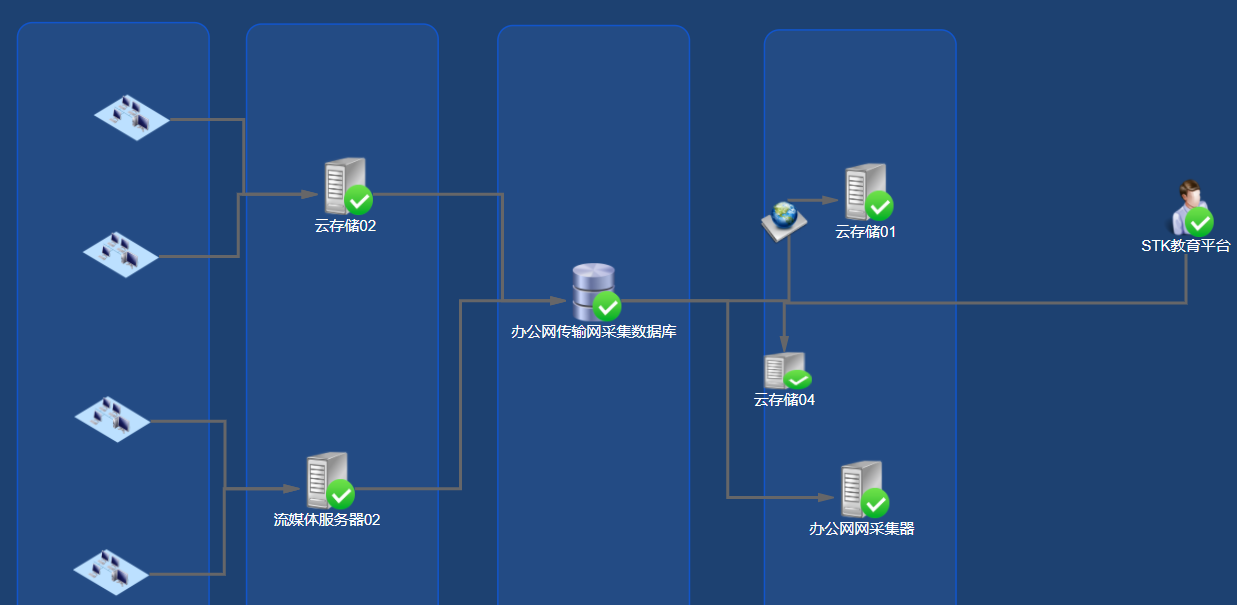
需求
看起来并不难,我们把资源的状态由高到低分为致命、严重、警告三个级别,整个业务系统的状态受最严重节点的影响,例如:如果业务系统中有一个资源的状态是致命,那么整个业务系统就是致命。
然而需求方有很多项目采用了负载均衡或分布式部署,某个节点宕机并不影响整个系统继续运行,这种简的单规则并不能有效判断系统的整体运行状态。
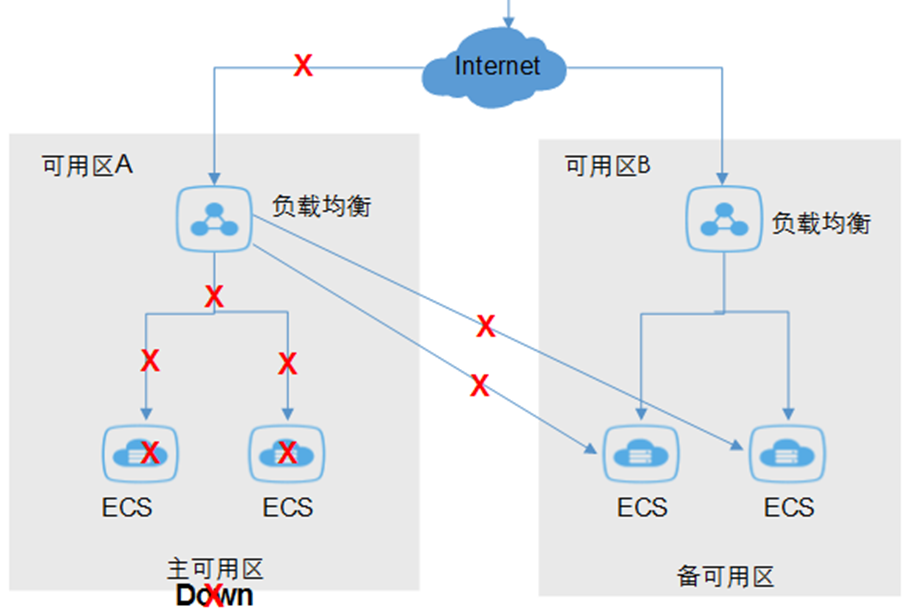
在上图中,虽然可用区A挂掉了,但整个系统依旧在运行,不能简单地把整个系统判处死刑。看来“分数”的概念是必须的,需要对系统中的每个节点或集群进行打分,最终计算出整个系统的分数,再根据预先设定的阈值判断系统的最终状态。
方案
针对这种情况,我们设计了三种表达式:MIN(取集群的最小值)、MAX(取集群的最大值)、AVG(取集群的加权平均)。具体来说,每个表达式计算的是一个集群的分数,当然,一个集群可以只包含一个节点,也可以包含其他集群。这样一来,上图可以用下面的表达式计算:
AVG(可用区A * 1, 可用区B * 1)
= AVG(MAX(ECSA1, ECSA2) * 1, MAX(ECSB1, ECSB2) * 1)
其中“* 1,”表示权重是1,对于上式来说,可用区A和可用区B权重相同。上式等于:
AVG(MAX(20, 20) * 1, MAX(100, 100) * 1) = (20 + 100) / (1 + 1) = 60
业务的健康度是60分,将产生一个相应级别的告警。
根据这种规则,可以进行任意嵌套:
MAX(AVG(60*3, 70*2, MAX(40, 70) * 4), MAX(30, 40, AVG(30*3, 90*7)), 50)
接下来的问题是,代码在有较强可读性的前提下,怎样根据给出的表达式计算出结果?
算法
在发布任务前,我给出了几个测试用例:
AVG(AVG(10*2, 2*2) * 1, 20 * 10) = 19
MAX(MIN(10, 5),10,MAX(20,21) = 21
MAX(AVG(60*3, MAX(40, 70) * 4)) = 66
MAX(AVG(60*3, 70*2, MAX(40, 70) * 4), MAX(30, 40, AVG(30*3, 90*7))) = 72
AVG(30*3, 90*7, AVG(20*4, 30*4) * 1) = 68
10分钟后,一个远程工作的小伙伴领取了这个任务,并且很快提交了结果。
他的思路是将表达式转换为解析树:

这样一来,就可以自底向上逐步计算出结果。
或许可以继续向下解析,将60*3分解为:
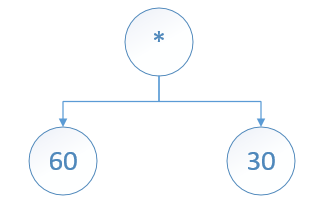
就这个项目来说,只有AVG涉及到加权运算符,因此这种分解没有必要。此外,对于集群的加权,比如 AVG(MAX(40,10) * 2),将被分解为:

对于AVG的子节点来说,要么是完整的表达式,比如a*b;或者被拆分成两个表达式,比如a和*b。在计算时,可以通过标准化处理,将所有a*b变为a和*b,最终保证AVG的叶子结点一定是偶数个,且每两个都能组成一对。
表达式是一个字符串,由三种元素构成:运算符(AVG, MAX, MIN, 乘号)、分隔符(左右括号,逗号)、数字,因此定义了下面的静态变量:
1 /* 2 * 自定义规则中的符号, 其中 MAX, MIN, AVG 是运算符, WEIGHT是加权符号 3 */ 4 final static public String MAX = "MAX"; //求最大 5 final static public String MIN = "MIN"; //求最小 6 final static public String AVG = "AVG"; //加权平均 7 final static public String WEIGHT = "*"; //加权乘法 8 final static public String SEPERATOR = ","; 9 final static public String BRACKETS_L = "("; 10 final static public String BRACKETS_R = ")";
之后通过遍历字符串的方式识别出节点,将节点插入解析树,主要代码如下:
1 static OPTree build(String expression) { 2 // 表达式语法树 3 OPTree tree = null; 4 // 语法树的当前节点 5 OPTree.Node currentNode = null; 6 String sign = ""; // 运算符标记 7 String num = ""; // 数字标记 8 // 表达式示例: MAX(10,-1,30,MIN(40,50),AVG(60*3, 70*2)) 9 // 将 "MAX(10,2)*4" 转换为 "MAX(10,2),*4", 从而让MAX(10,2)和"*4"平级,简化处理 10 char[] chars = expression.replaceAll(" ", "").replaceAll("\)\*", "),\*").toCharArray(); 11 for(char c : chars) { 12 if(('0' <= c && c <= '9') || c == WEIGHT.charAt(0)) { 13 num += c; 14 continue; 15 } 16 17 sign += c; 18 // 1. 遇到MAX, MIN, AVG,将其作为根节点插入语法树,并将currentNode指向它; 19 switch (sign) { 20 case MAX: 21 case MIN: 22 case AVG: 23 if (tree == null) { 24 tree = new OPTree(sign); 25 currentNode = tree.getRoot(); 26 } else { 27 currentNode = tree.insert(sign, currentNode); 28 } 29 sign = ""; 30 break; 31 // 2. 遇到“(”, 直接将运算符标记和数字符标记清空 32 case BRACKETS_L: 33 sign = ""; 34 num = ""; 35 break; 36 // 3. 遇到“,”: 37 // 3.1 如果num非空, 直接将num作为currentNode的叶子节点 38 // 3.2 如果num为空,直接将currentNode指向上一层节点 39 case SEPERATOR: 40 assert currentNode != null; 41 if (!num.isEmpty()) { 42 tree.insertChild(valueTranse(num), currentNode); 43 } else { 44 currentNode = currentNode.getParent(); 45 } 46 num = ""; 47 sign = ""; 48 break; 49 // 4. 遇到 “)”, 50 // 4.1 如果num非空,先将num作为currentNode的叶子节点 51 // 4.2 如果num为空,直接将currentNode指向上一层节点 52 case BRACKETS_R: 53 assert tree != null; 54 if (!num.isEmpty()) { 55 tree.insertChild(valueTranse(num), currentNode); 56 } 57 else { 58 currentNode = currentNode.getParent(); 59 } 60 num = ""; 61 sign = ""; 62 break; 63 } 64 } 65 66 return tree; 67 }
如果去掉注释和一些预先设置好的静态变量,核心代码约为50行,这可比反复使用正则表达式匹配漂亮多了。
算法预先定义了curentNode作为解析树的当前节点,用sign和num记录表达式的符号和数字,从左到右遍历表达式中的每一个字符:
0. 遇到数字或"-",拼接到num末尾;
1. 遇到MAX, MIN, AVG,将其作为根节点插入语法树,并将currentNode指向它,再将sign清空;
2. 遇到“(”, 直接将sign和num清空;
3. 遇到“,”,如果num非空, 直接将num作为currentNode的叶子节点,否则直接将currentNode指向上一层节点;之后将sign和num清空;
4. 遇到 “)”, 如果num非空,先将num作为currentNode的叶子节点,否则直接将currentNode指向上一层节点;之后将sign和num清空;
当遍历过最后一个节点后,解析树构造完成。
以MAX(10,-1,30,MIN(40,50),AVG(60*3, 70*2))为例,验证整个过程:
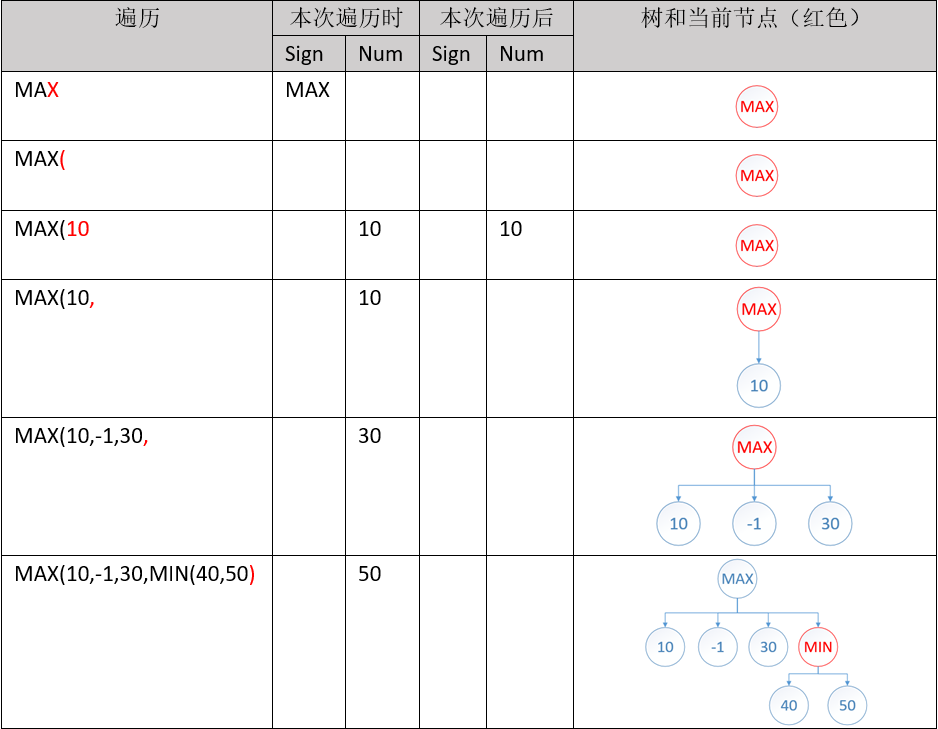

最终,curentNode将指向解析树的根节点。
有了解析树后,就可以通过后序遍历,自底向上算出整个业务系统的分值。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”
