什么是拉格朗日中值定理
如果两地的距离是600公里,驾车走完这600公里耗时6小时,那么在某一时刻,你的速度必定会达到平均速度100公里/小时。
上述问题转换成数学语言:f(x)是距离关于时间的函数,那么一定存在:
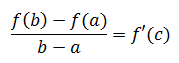
f’(c)就是c时刻的瞬时速度。前提条件是f(x)在[a, b]上连续,f(x)在(a,b)内可导,且 a < c < b。这就是拉格朗日中值定理的通俗定义。
中值定理的几何意义如下图所示:

在曲线的两点间做一条割线,割线的斜率就是(f(b)-f(a))/(b-a), f’(c)是与割线平行的一条切线,与曲线相切于c点。
需要注意的是中值定理的前提条件,下面的曲线不满足中值定理:
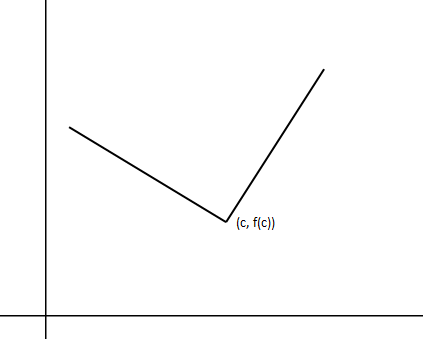
函数虽然是连续的,但在x=c点处不可导,中值定理要求函数在定义域范围内全部可导。
推论
- 如果f’>0,则f递增
- 如果f’<0,则f递减
- 如果f’=0,则f是常数
其中1,2在数学笔记7——曲线构图中使用过,在讨论函数凹凸性时运用了这两个结论。现在用中值定理给出推论的证明。
证明推论1:
中值定理公式:

由于b>a,f’>0,所以f(b)-f(a)>0,f(b)>f(a),故f递增。
推论2,3的证明与1类似。
示例
示例1:ex > 1+x
证明当x > 0时,ex >1+x
令f(x) = ex – (1 + x),f’(x) = ex – 1
f’(x)单调递增,f’(0) = 0
∴ x > 0 时,f’(x) > 0,f(x) = ex – (1 + x)递增
∵ f(0) = 0,f(x)在x > 0上递增
∴ ex > 1 + x
示例2:ex > 1+x+x2/2
证明当x > 0时,ex >1+x+x2/2
令f(x) = ex – (1 + x + x2/2),f’(x) = ex – (1 + x)
示例1已经证明f’(x) > 0, 所以f(x)是递增的
f(0) = 0, x>0时,f(x) > 1,ex >1+x+x2/2
示例3:tanx > x
证明当0 < x < π/2时,tanx > x
设f(x) = tanx,f’(x)=sec2x根据中值定理:
f(b) = f(a) + f’(c)(b – a), a < c < b
令 a = 0, x = b <π/2
f(x) = f(0) + f’(c)(x – 0) = xsec2c = tanx
当 0 < c <π/2时,sec2c = 1/cos2c > 1
∴ tanx > x
也可以令f(x) = tanx – x, f’(x) = sec2x – 1 > 0 => f(x)在定义域内递增,tanx > x
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”
