微分在数学中的定义:由函数B=f(A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx处的极限叫作函数在dx处的微分,微分的中心思想是无穷分割。积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说,对于一个给定的正实值函数,在一个实数区间上的定积分可以理解为在坐标平面上,由曲线、直线以及轴围成的曲边梯形的面积值(一种确定的实数值)。
微分
什么是微分
如果对于函数y=f(x),存在dy=f’(x)dx,称dy是y的微分或f(x)的微分。
如果换一种写法:
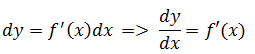
这实际上就是莱布尼茨对于导数的记法,它和导数表达了同一个意思。
重新审视导数的含义,其公式:
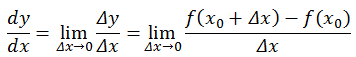
导数表示的是两个无穷小量的比,dy和dx就是这两个无穷小量:
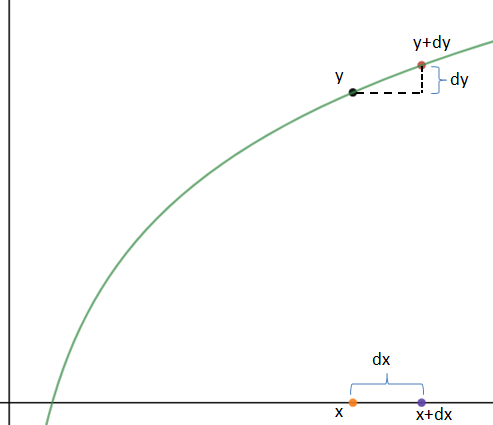
过去我们把dy和dx叫做Δy和Δx,实际上它们不是一回事,Δx是一个实实在在的数量,dx是一个概念,是Δx→0的函数表达式,可以把dx看作一个符号,就是微分符号。
用微分求解近似值
示例:64.11/3≈?
设y = x1/3,当x = 64时,y = 4,x + dx = 64.1,dx = 0.1,代入微分公式:

微分法与线性近似的对比
示例也可以用线性近似法求解。设f(x) = x1/3,x0 = 64
根据线性近似公式:
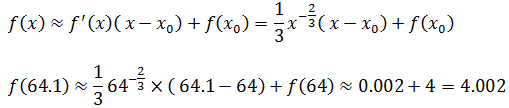
两种方法的结果相同。结合线性近似公式和微分公式:
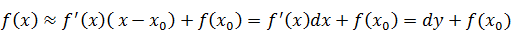
实际上线性近似是微分的一种应用。
示例
示例1,d(7x9 + 34 – 5u-3) = ?
根据导数的加法法则,
d(7x9 + 34 – 5u-3) = d(7x9) + d(34) – d(5u-3) = 7×9x8dx + 0 – 5×(-3)x-4dx = 63x8dx + 15x4dx
示例2,d(sinθcosθ) = ?
根据导数的乘法法则,
d(sinθcosθ) = (dsinθ)cosθ + sinθdcosθ = (cos2θ-sin2θ)dθ
示例3,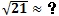
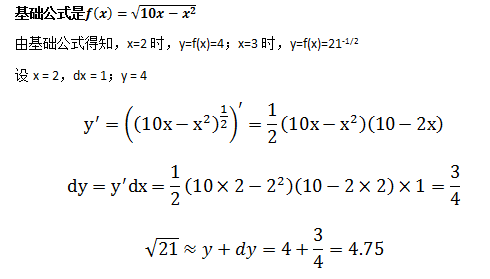
不定积分
什么是不定积分

上面的式子就是不定积分表达式,称作g(x)dx的不定积分,其中G(x)的导数是g(x),即G(x)是g(x)的反导数。g(x)的反导数又叫做g的不定积分,∫就是积分符号。
示例1,∫sinxdx
求解sinxdx的不定积分,实际上是求解谁的导数是sinx。如果G(x)=-cosx,则G’(x)=sinx,所以∫sinxdx = -cosx + C,其中C是一个常数,之所以叫不定积分,就是因为有了这个常数。∫sinxdx是不定的,因为我们并没有给出一个确定的函数。
示例2,∫xadx
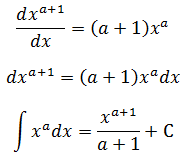
示例3,∫dx/x
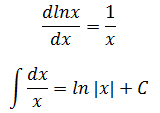
不定积分的唯一性
不定积分的唯一性:如果f’(x)=g’(x),则f(x) = g(x) + c
以下给出证明:
设F=f(x),G=g(x),如果f’(x)=g’(x),则(F – G)’ = F’ – G’ = 0
常数的导数是0,所以F-G是一个常数,即f(x) – g(x) = c => f(x) = g(x) + c,证毕。
唯一性也是不定积分成立的基础。
求解不定积分
不定积分的求解远比求导困难的多,很多时候甚至发现根本无法求解,这里仅记录两种最常用的求解方法:换元法和猜测法。
换元法
示例1,∫x3(x4+2)5dx
这个不能一眼看出答案了,使用一种称为换元法的方法求解。
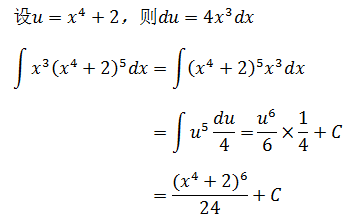
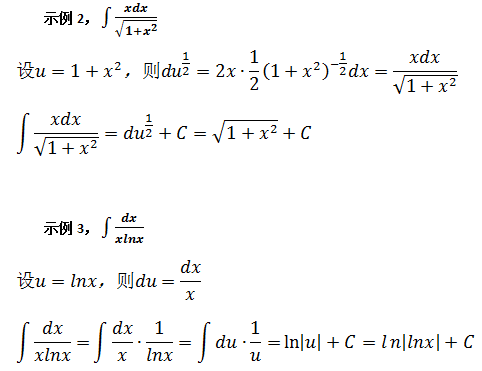
猜测法
做过大量练习后就可以使用猜测法直接猜测不定积分的结果,这应该成为首先尝试的求解方法。
示例1,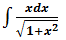
这个例子在换元法中出现过,现在使用猜测法求解。
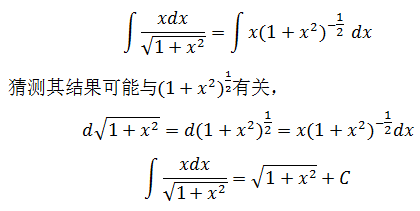
示例2,∫e6xdx

示例3 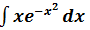
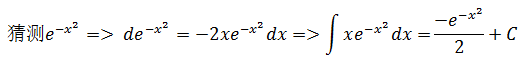
示例4,∫sinxcosxdx
猜测sin2x => dsin2x = 2sinxcosxdx => ∫sinxcosxdx = sin2x/2 + C1
∫sinxcosxdx的另一个答案是 -cos2x/2 + C2
如果将两个答案相减,得到(sin2x+ cos2x)/2 + (C1 - C2) = 1/2 + (C1 - C2) = C,两个函数的相减的结果是一个常数,即这两个函数是同族函数。
综合示例
示例1,d(7x9 + 34 – 5u-3) = ?
根据导数的加法法则,
d(7x9 + 34 – 5u-3) = d(7x9) + d(34) – d(5u-3) = 7×9x8dx + 0 – 5×(-3)x-4dx = 63x8dx + 15x4dx
示例2,d(sinθcosθ) = ?
根据导数的乘法法则,
d(sinθcosθ) = (dsinθ)cosθ + sinθdcosθ = (cos2θ-sin2θ)dθ
示例3,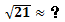

示例4,
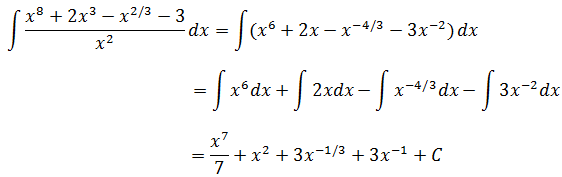
示例5,∫e2xcos(1-e2x)dx
使用换元法,令u = (1-e2x), du = -2 e2xdx
∫e2xcos(1-e2x)dx =∫cos(1-e2x) e2xdx =∫u (-1/2)du = -sinu/2 + C = -sin (1-e2x)/2 + C
示例6,∫4x(5x2-1)1/3dx
这个又要靠猜测法了,猜的(5x2-1)1/3的反导数。
d(5x2-1)4/3 = (4/3) (5x2-1)1/3(10x)dx = (40/3)x(5x2-1)1/3dx,与目标很相似
∫4x(5x2-1)1/3dx = (3/10)(5x2-1)4/3 + C
示例7,∫tanxdx
∫tanxdx = ∫(sinx/cosx)dx
使用换元法,令u = cosx, du = -sinxdx
∫(sinx/cosx)dx = ∫-du/u = -ln|u| + C = -ln|cosx| + C
积分表
以下是25个基本不定积分公式:
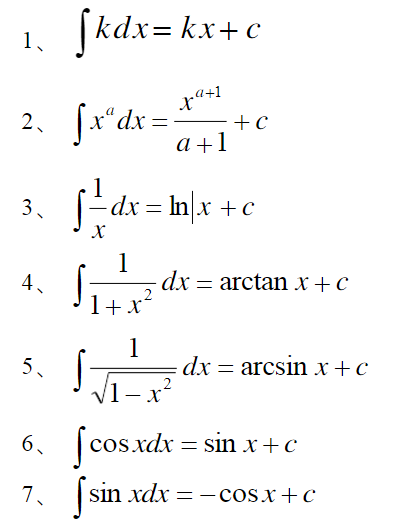
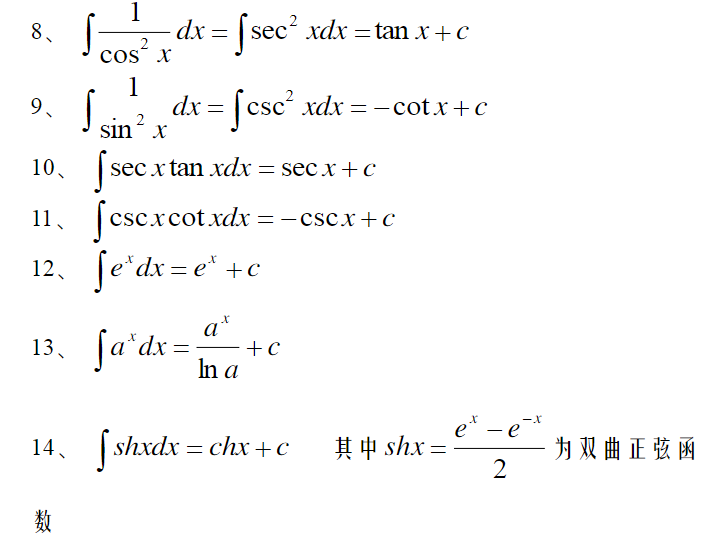
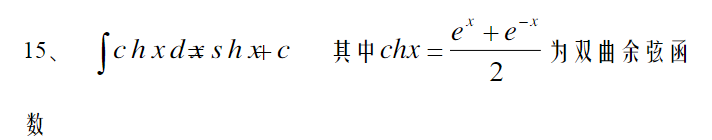
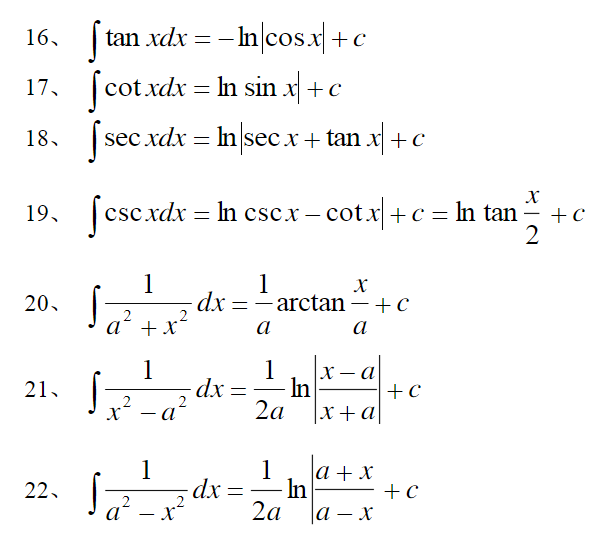
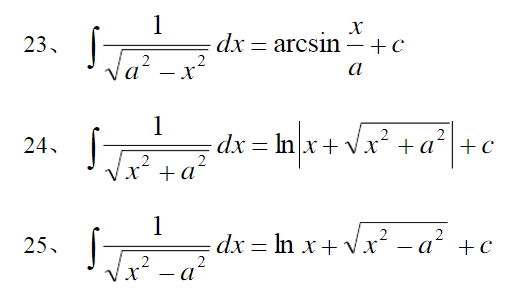
总结
1.微分表达式:dy = f’(x)dx
2.不定积分表达式:G(x) = ∫g(x)dx
3.不定积分的唯一性:如果f’(x)=g’(x),则f(x) = g(x) + c
4.用换元法和猜测法求解不定积分
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”
