单变量微积分笔记15——微积分第二基本定理

微积分第二基本定理

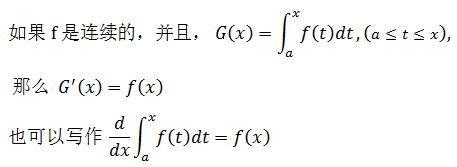
　　这里需要注意t与x的关系，它的意思是一个函数能够找到相应的积分方式去表达。如果F’=f，则：

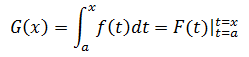
　　下面是第二基本定理的证明。

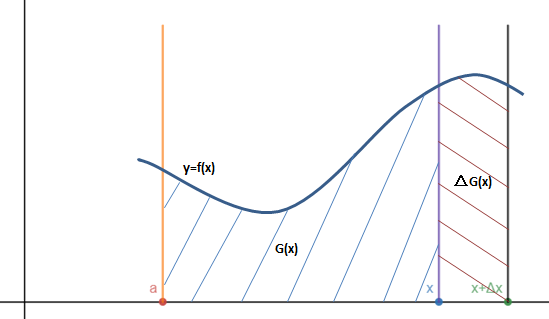
　　证明需要采用画图法，如上图所示，曲线是y=f(x)，两个阴影部分的面积分别是G(x)和ΔG(x)，其中：

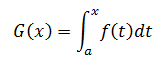
　　当Δx足够小时：

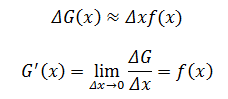
示例1

　

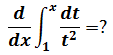
　　根据微积分第二基本定理：

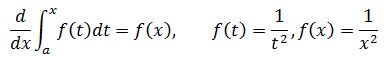
　　下面做一下验证：

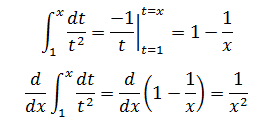
示例2

　　解微分方程， L’(x) = 1/x; L(1) = 0

　　按照以往的求解方式：

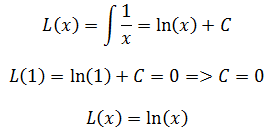
　　现在根据微积分第二基本定理，可以直接写作：

 

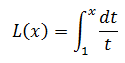
　　这种表达式其实是比过去的对数形式更有效的一种表达。

第二基本定理的链式法则

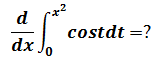
　　由于积分上界是x²，所以不符合标准的第二基本定理，求解这类问题的一般步骤是使用链式法则求解。

 

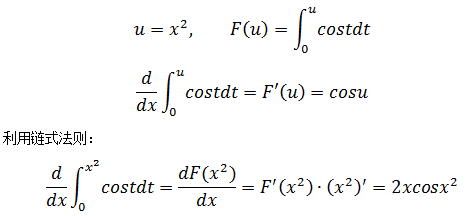
　　这种求解方法具有通用性，积分上界是任何函数都可以用该方法求解。

超越函数

　　微积分第二基本定理可以得出很多新函数。下面是一个例子：

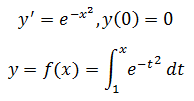
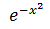　　就是著名的高斯函数。

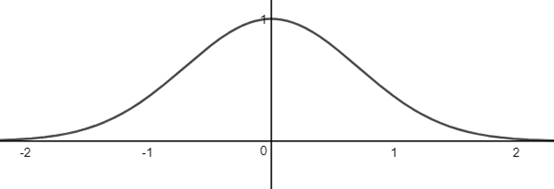
　　f(x)表示x>=0时，曲线与x轴的面积，f(x)就是一个超越函数。超越函数最有趣的地方是，它不能用过去的任何代数函数表示出来，包括对数、指数、三角函数等，只有用微积分才能有效地表达。下图就是一个超越函数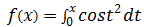的曲线：

  

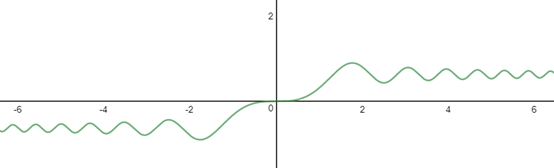
综合示例

示例1 

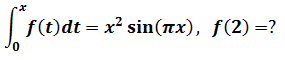
　　根据第二基本定理，

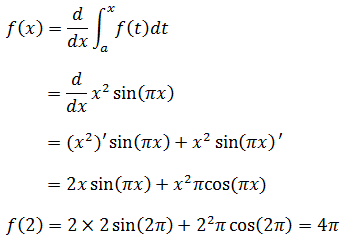
示例2

　　首先来看二阶近似的定义（关于近似和二阶近似可参考数学笔记6——线性近似和二阶近似）：

　　当x≈x₀=0时

 

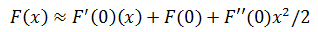
　　对于本例：

 

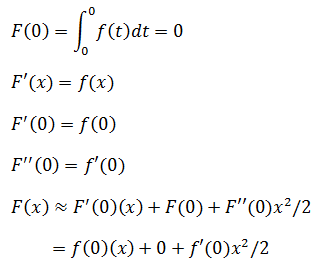
　　前提条件是f在0附近是可微的。

 

---

　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”