欧拉函数
-
1~N中与N互质的数的个数被称为欧拉函数,记为φ(n)
-
若a,b的最大公约数为1,那么a,b互质
-
根据容斥原理,推出计算欧拉函数的式子
-
设p是N的质因子,1 ~ N中p的倍数有N/p个,同理,若q也是N的质因子,1 ~ N中的q的倍数有N/q个
-
如果我们把p和q的倍数去掉,那么p*q的倍数被去掉了两次,需要再加回来一次
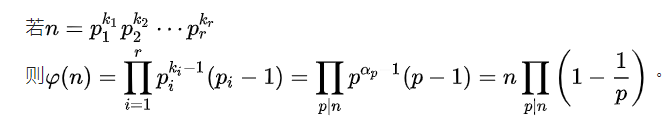
代码如下:
- 根据欧拉函数的计算式,只需要分解质因数,就可以求出欧拉函数#
int phi(int n){
int ans = n;
for(int i = 2; i <= n/i; i ++ ){
if(n % i == 0){
ans = ans / i * (i - 1);
while(n % i == 0) n /= i;
}
}
if(n > 1) ans = ans / n * (n - 1);
}
其他性质:
- 1~n中与n互质的数的和为n*φ(n)/2。
- 若m,n互质,φ(mn)=φ(m)φ(n)。
利用埃氏筛法,求出2~N中每个数的欧拉函数
void get_euler(int n){
for(int i = 2; i <= n; i ++ ){
phi[i] = i;
}
for(int i = 2; i <= n; i ++ ){
if(phi[i] == i){
for(int j = i; j <= n; j += i) phi[j] = phi[j] / i * ( i - 1);
}
}
}
利用线性筛法,求出2~N中每个数的欧拉函数
int primes[N],cnt;//所有质数
int phi[N];//所有i对应的欧拉函数
int st[N];//存放最小质因子
void get_euler(int n){
phi[1] = 1;
for(int i = 2; i <= n; i ++){
if(!st[i]) st[i] = i,primes[++ cnt] = i,phi[i] = i - 1;
for(int j = 1; j <= cnt; j ++ ){
//i有比prime[j]更小的质因子,或者超出n的范围,停止循环
if(primes[j] > st[i] || primes[j] > n/i) break;
//primes[j]是合数i*primes[j]的最小质因子
int t = i * primes[j];
st[t] = primes[j];
if(i % primes[j] == 0){
phi[t] = phi[i] * primes[j];
}else{
phi[t] = phi[i] * (primes[j] - 1);
}
}
}
}
欧拉定理

费马小定理

逆元

快速幂求逆元

#include<bits/stdc++.h>
using namespace std;
#define mm(a,x) memset(a,x,sizeof a)
#define mk make_pair
#define ll long long
#define pii pair<int,int>
#define inf 0x3f3f3f3f
#define lowbit(x) (x) & (-x)
#define endl "
"
const int N = 1e5 + 10;
ll n,p;
ll res;
inline ll qmi(ll a,ll b,ll p){
ll ans = 1;
a%=p;
while(b){
if(b&1) ans = ans * a % p;
a = a * a % p;
b >>= 1;
}
return ans%p;
}
int main() {
scanf("%lld%lld",&n,&p);
for(ll i = 1; i <= n; i ++ ){
res = qmi(i,p - 2,p);
printf("%lld
",res);
}
return 0;
}