#include <stdio.h>
int i=0;
void move(int n,char a,char b){
printf("move %d from %c to %c
",n,a,b);
i++;
}
void hanoi(int n,char a,char b,char c){
if(n==1)
move(1,a,c);
else
{
hanoi(n-1,a,c,b);
move(n,a,c);
hanoi(n-1,b,a,c);
}
}
int main(){
hanoi(5,'a','b','c');
printf("%d",i);
return 0;
}
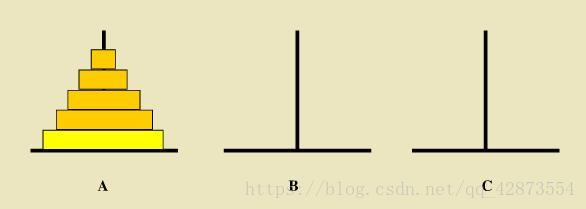
所写hanio()方法的作用是使一堆 从一个柱子移到另一个柱子(过程中需要一个辅助柱)
问题核心:假设从上到下是第1-n个 , 最后几步一定是把第n个上的n-1个从A移到B, 然后把 第n个从A移到C ,然后把B的n-1个从B移到C(移动一堆时均要辅助柱子),问题出口为一个盘子时从A移到C(个人感觉类似科学计数法)
递归:
使用条件:重复相似的过程,将复杂问题化为子问题求解
无法解决->存入栈中->还无法解决->继续存入栈中->……直到能够解决逆向一步一步返回数据 还原场景
递归 每一次都转化为子问题,向递归出口靠近
个人理解:类似于科学计数法 最简单的条件成立 然后一般条件成立(n=1递归过程成立 n=x 递归过程仍成立)
递归中函数如何入栈出栈:
个人理解:main函数进入子函数 , 子函数再进入子函数, 子函数进入子子函数之前 都要把返回地址 和参数 保存 ,然后转入子函数 ,直到不再调用就把值传回