计算矩的目的
从一幅图像计算出来的矩集,不仅可以描述图像形状的全局特征,而且可以提供大量关于该图像不同的几何特征信息,如大小,位置、方向和形状等。这种描述能力广泛应用于各种图像处理、计算机视觉和机器人技术领域的目标识别与方位估计中。同时矩函数在图像分析中也有着广泛的应用,如模式识别、目标分类、目标识别与方位估计、图像的编码与重构等。
矩的计算:moments 函数
moments 函数可以很方便的计算出多边形区域的最高三阶空间矩,中心矩和归一化中心矩。
Moments moments(InputArray array, bool binnaryImage = false);
- array,一幅 8 位、单通道图像,或一个二维浮点数组(Point of Point2f)。
- binnaryImage,是否为二值图像。默认为 false。若此值为 true,则所有非零像素均为 1,需注意的是,此参数仅对图像使用。
- 返回值为 Moments 类型对象(矩)
几种常见矩:空间矩/几何矩、中心距、归一化中心距、Hu矩
空间矩/几何矩
空间矩的实质为面积或者质量。可以通过一阶矩计算质心/重心。
空间矩计算公式: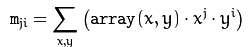 其中(i+j)等于几就叫几阶矩。
其中(i+j)等于几就叫几阶矩。
重心计算公式(中心 centers):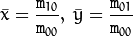
中心距
中心矩体现的是图像强度的最大和最小方向(中心矩可以构建图像的协方差矩阵),其只具有平移不变性,所以用中心矩做匹配效果不会很好。
中心距计算公式:
归一化中心矩
归一化后具有尺度不变性。
归一化中心距计算公式: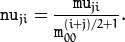
Hu矩
Hu矩具有尺度、旋转、平移不变性,可以用来做匹配。
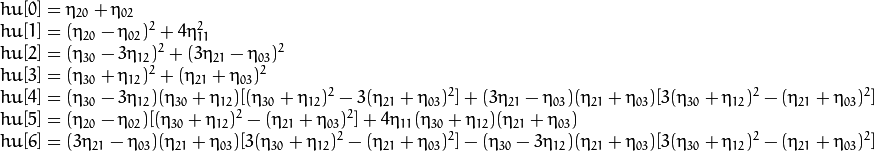
借鉴博客:https://www.cnblogs.com/fcfc940503/p/11319251.html