数据结构--栈和队列

基本概念

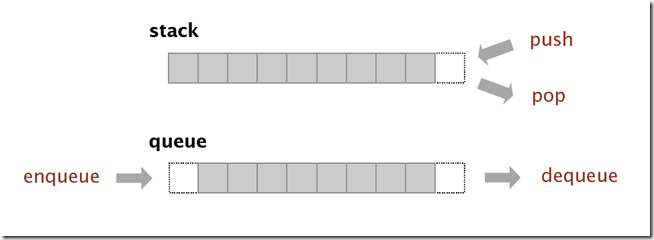
　　栈(Stack)是一种后进先出(last in first off,LIFO)的数据结构；

　　队列(Queue)是一种先进先出(first in first out,FIFO)的结构；

　　

实现

　　现在来看如何实现以上两个数据结构。

　　Stack的实现

　　　　栈是一种后进先出的数据结构，对于Stack我们希望至少要对外提供以下几个方法：

　　　　

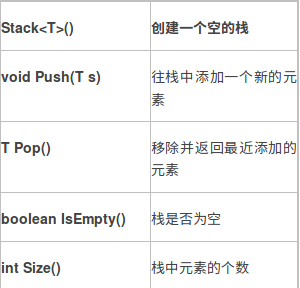
　　要实现这些功能，我们有两种方法，数组和链表。

栈的链表实现

　　我们首先定义一个内部类来保存每个链表的节点，该节点包括当前的值以及指向下一个的值，然后建立一个节点保存位于栈顶的值以及记录栈的元素个数：

class Node
{
    public T Item{get;set;}
    public Node Next { get; set; }
}

private Node first = null;
private int number = 0;

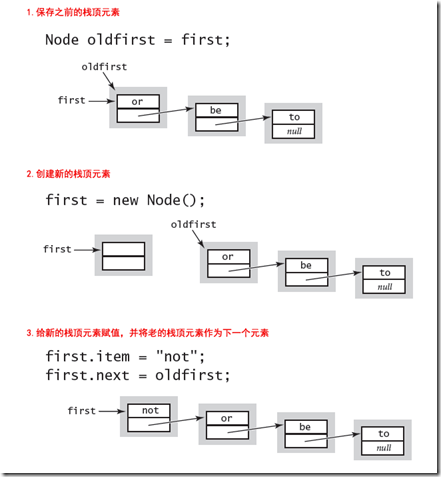
　　现在来实现Push方法，即向栈顶压入一个元素，首先保存原先的位于栈顶的元素，然后新建一个栈顶元素，然后将该元素的下一个指向原先的栈顶元素。

　　

　　

void Push(T node)
{
    Node oldFirst = first;
    first = new Node();
    first.Item= node;
    first.Next = oldFirst;
    number++;
}

Pop方法也很简单，首先保存栈顶元素的值，然后将栈顶元素设置为下一个元素：

　　

　　　　

T Pop()
{
    T item = first.Item;
    first = first.Next;
    number--;
    return item;
}

　　基于链表的Stack实现，在最坏的清空下只需要常量的时间来进行Push和Pop操作

　　栈的数组实现：

　　　　我们可以使用数组来存储栈中的元素Push的时候，直接添加一个元素S[N]到数组中，Pop的时候直接返回S[N-1]

　　

　　首先，我们定义一个数组，然后在构造函数中给定初始化大小，Push方法实现如下，就是集合里添加一个元素：

　　

T[] item;
int number = 0;

public StackImplementByArray(int capacity)
{
    item = new T[capacity];
}

public void Push(T _item)
{
    if (number == item.Length) Resize(2 * item.Length);
    item[number++] = _item;
}

Pop方法：

　　

public T Pop()
{
    T temp = item[--number];
    item[number] = default(T);
    if (number > 0 && number == item.Length / 4) Resize(item.Length / 2);
    return temp;
}

　　在Push和Pop方法中，为了节省内存空间，我们会对数组进行整理。Push的时候，当元素的个数达到数组的Capacity的时候，我们开辟2倍于当前元素的新数组，然后将原数组中的元素拷贝到新数组中。Pop的时候，当元素的个数小于当前容量的1/4的时候，我们将原数组的大小容量减少1/2。

　　Resize方法基本就是数组复制：

private void Resize(int capacity)
{
    T[] temp = new T[capacity];
    for (int i = 0; i < item.Length; i++)
    {
        temp[i] = item[i];
    }
    item = temp;
}

　　当我们缩小数组的时候，采用的是判断1/4的情况，这样效率要比1/2要高，因为可以有效避免在1/2附件插入，删除，插入，删除，从而频繁的扩大和缩小数组的情况。下图展示了在插入和删除的情况下数组中的元素以及数组大小的变化情况：

　　

 　　

分析：

　　1. Pop和Push操作在最坏的情况下与元素个数成比例的N的时间，时间主要花费在扩大或者缩小数组的个数时，数组拷贝上。

　　2. 元素在内存中分布紧凑，密度高，便于利用内存的时间和空间局部性，便于CPU进行缓存，较LinkList内存占用小，效率高。

 Queue的实现

 　　Queue是一种先进先出的数据结构，和Stack一样，他也有链表和数组两种实现，理解了Stack的实现后，Queue的实现就比较简单了。

 　　

　　

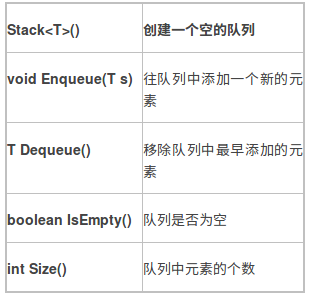
　　首先看链表的实现：

 　　Dequeue方法就是返回链表中的第一个元素，这个和Stack中的Pop方法相似：

　　

public T Dequeue()
{
    T temp = first.Item;
    first = first.Next;
    number--;
    if (IsEmpety())
        last = null;
    return temp;
}

　　Enqueue和Stack的Push方法不同，他是在链表的末尾增加新的元素：

　　

public void Enqueue(T item)
{
    Node oldLast = last;
    last = new Node();
    last.Item = item;
    if (IsEmpety())
    {
        first = last;
    }
    else
    {
        oldLast.Next = last;
    }
    number++;
}

　　同样地，现在再来看如何使用数组来实现Queue，首先我们使用数组来保存数据，并定义变量head和tail来记录Queue的首尾元素。

　　

　　

　　和Stack的实现方式不同，在Queue中，我们定义了head和tail来记录头元素和尾元素。当enqueue的时候，tial加1，将元素放在尾部，当dequeue的时候，head减1，并返回。

　　

public void Enqueue(T _item)
{
    if ((head - tail + 1) == item.Length) Resize(2 * item.Length);
    item[tail++] = _item;
}

public T Dequeue()
{
    T temp = item[--head];
    item[head] = default(T);
    if (head > 0 && (tail - head + 1) == item.Length / 4) Resize(item.Length / 2);
    return temp;
}

private void Resize(int capacity)
{
    T[] temp = new T[capacity];
    int index = 0;
    for (int i = head; i < tail; i++)
    {
        temp[++index] = item[i];
    }
    item = temp;
}

 

Stack和Queue的应用

　　Stack这种数据结构用途很广泛，比如编译器中的词法分析器、Java虚拟机、软件中的撤销操作、浏览器中的回退操作，编译器中的函数调用实现等等。

　　线程堆 (Thread Stack)

　　　　线程堆是操作系型系统分配的一块内存区域。通常CPU上有一个特殊的称之为堆指针的寄存器 (stack pointer) 。在程序初始化时，该指针指向栈顶，栈顶的地址最大。CPU有特殊的指令可以将值Push到线程堆上，以及将值Pop出堆栈。每一次Push操作都将值存放到堆指针指向的地方，并将堆指针递减。每一次Pop都将堆指针指向的值从堆中移除，然后堆指针递增，堆是向下增长的。Push到线程堆，以及从线程堆中Pop的值都存放到CPU的寄存器中

　　　　当发起函数调用的时候，CPU使用特殊的指令将当前的指令指针(instruction pointer)，如当前执行的代码的地址压入到堆上。然后CPU通过设置指令指针到函数调用的地址来跳转到被调用的函数去执行。当函数返回值时，旧的指令指针从堆中Pop出来，然后从该指令地址之后继续执行。

　　　　当进入到被调用的函数中时，堆指针减小来在堆上为函数中的局部变量分配更多的空间。如果函数中有一个32位的变量分配到了堆中，当函数返回时，堆指针就返回到之前的函数调用处，分配的空间就会被释放。

　　　　

　　　　如果函数有参数，这些参数会在函数调用之前就被分配在堆上，函数中的代码可以从当前堆往上访问到这些参数。

　　　　线程堆是一块有一定限制的内存空间，如果调用了过多的嵌套函数，或者局部变量分配了过多的内存空间，就会产生堆栈溢出的错误。

　　　　下图简单显示了线程堆的变化情况　　

 　　　　

　　算术表达式的求值

　　

　　　　Stack使用的一个最经典的例子就是算术表达式的求值了，这其中还包括前缀表达式和后缀表达式的求值。E. W. Dijkstra发明了使用两个Stack，一个保存操作值，一个保存操作符的方法来实现表达式的求值，具体步骤如下：

　　　　1) 当输入的是值的时候Push到属于值的栈中。

　　　　2) 当输入的是运算符的时候，Push到运算符的栈中。

　　　　3) 当遇到左括号的时候，忽略

　　　　4) 当遇到右括号的时候，Pop一个运算符，Pop两个值，然后将计算结果Push到值的栈中。

　　　　下面是在C#中的一个简单的括号表达式的求值：

/// <summary>
/// 一个简单的表达式运算
/// </summary>
/// <param name="args"></param>
static void Main(string[] args)
{
    Stack<char> operation = new Stack<char>();
    Stack<Double> values = new Stack<double>();
    //为方便，直接使用ToChar对于两位数的数组问题
    Char[] charArray = Console.ReadLine().ToCharArray();

    foreach (char s in charArray)
    {
        if (s.Equals('(')) { }
        else if (s.Equals('+')) operation.Push(s);
        else if (s.Equals('*')) operation.Push(s);
        else if (s.Equals(')'))
        {
            char op = operation.Pop();
            if (op.Equals('+'))
                values.Push(values.Pop() + values.Pop());
            else if (op.Equals('*'))
                values.Push(values.Pop() * values.Pop());
        }
        else values.Push(Double.Parse(s.ToString()));
    }
    Console.WriteLine(values.Pop());
    Console.ReadKey();
}

运行结果如下：

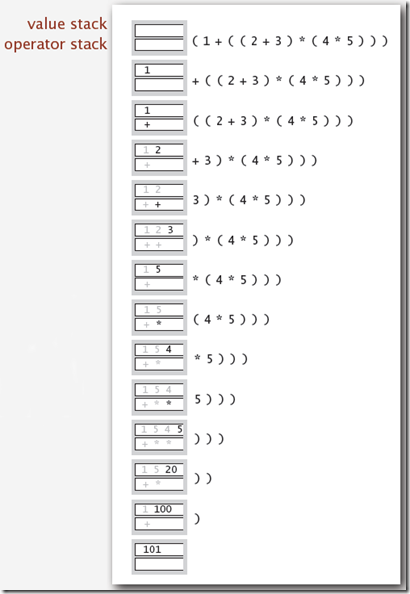
下图演示了操作栈和数据栈的变化。

在编译器技术中，前缀表达式，后缀表达式的求值都会用到堆。

Queue的应用

　　在现实生活中Queue的应用也很广泛，最广泛的就是排队了，”先来后到” First come first service ，以及Queue这个单词就有排队的意思。

　　还有，比如我们的播放器上的播放列表，我们的数据流对象，异步的数据传输结构(文件IO，管道通讯，套接字等)

　　还有一些解决对共享资源的冲突访问，比如打印机的打印队列等。消息队列等。交通状况模拟，呼叫中心用户等待的时间的模拟等等。