二叉查找树之AVL树

定义平衡树节点:

class TreeNode {

        /**
         * 树节点的值
         */
        private int val;

        /**
         * 树的高度
         */
        private int height;

        /**
         * 左子节点
         */
        private TreeNode left;

        /**
         * 右子节点
         */
        private TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }

    }

辅助的方法：

1.用于计算节点的高度：

/**
     * 获取节点的高度
     *
     * @param node
     * @return
     */
    private int height(TreeNode node) {
        return node == null ? -1 : max(height(node.left), height(node.right)) + 1;
    }

    /**
     * 获取二者中较大的
     *
     * @param a
     * @param b
     * @return
     */
    private int max(int a, int b) {
        return a >= b ? a : b;
    }

2.获取节点的平衡因子(即左子树与右子树的高度差)：

    /**
     * 获取节点的平衡因子
     *
     * @param node
     * @return
     */
    private int getBalanceFactor(TreeNode node) {
        return node == null ? -1 : height(node.left) - height(node.right);
    }

AVL树插入数据的四种结构：

第一种：

 只需要实现单次右旋：

    /**
     * 右旋
     * 返回旋转后新的节点
     * @param tree 待旋转的节点
     */
    private TreeNode rightRotate(TreeNode tree) {
        //拷贝源节点的左节点
        TreeNode node = tree.left;
        tree.left = node.right;
        node.right = tree;
        //重新计算节点的高度
        node.height = height(node);
//        tree.height = height(tree);
        tree = null; //help gc
        return node;
    }

第二种:

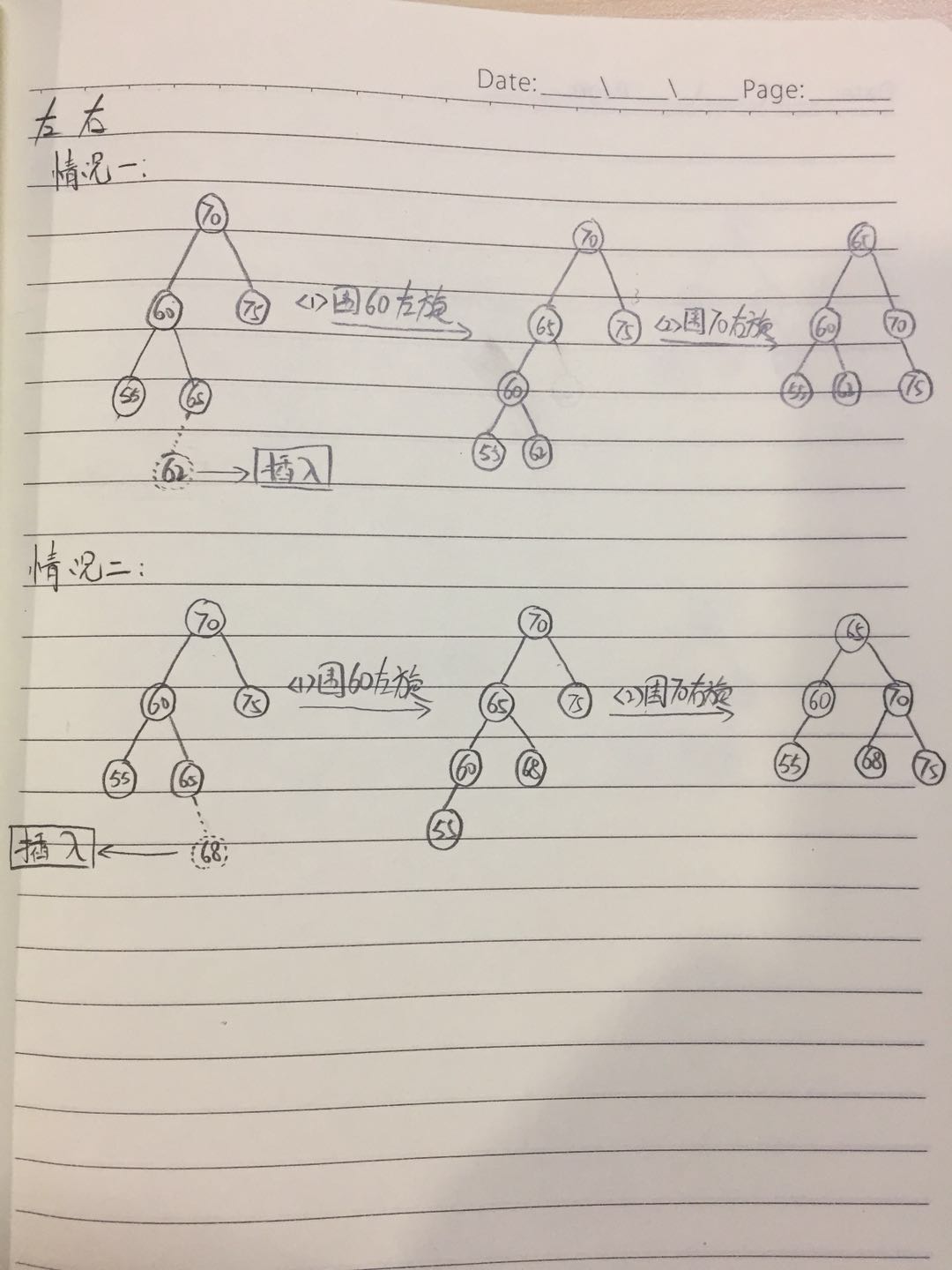
 先左旋节点的左子节点，再右旋节点：

//先左旋左节点，再右旋节点
node.left = leftRotate(node.left);
return rightRotate(node);

第三种:

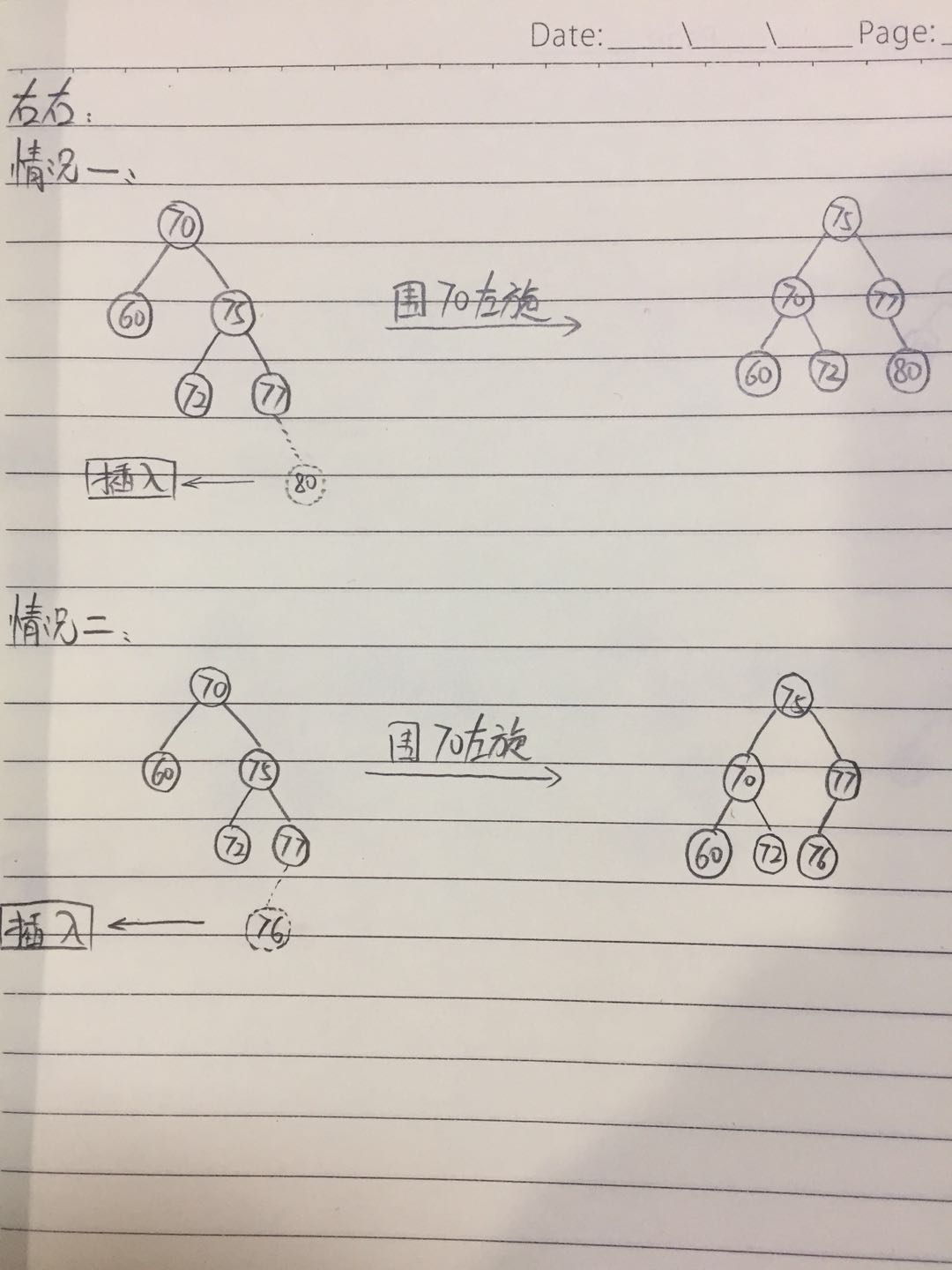
 只需要实现单次左旋：

   /**
     * 左旋
     *
     * @param tree 待旋转的节点
     */
    private TreeNode leftRotate(TreeNode tree) {
        TreeNode node = tree.right;
        tree.right = node.left;
        node.left = tree;
        //重新计算节点的高度
        node.height = height(node);
//        tree.height = height(tree);
        tree = null; //help gc
        return node;
    }

第四种:

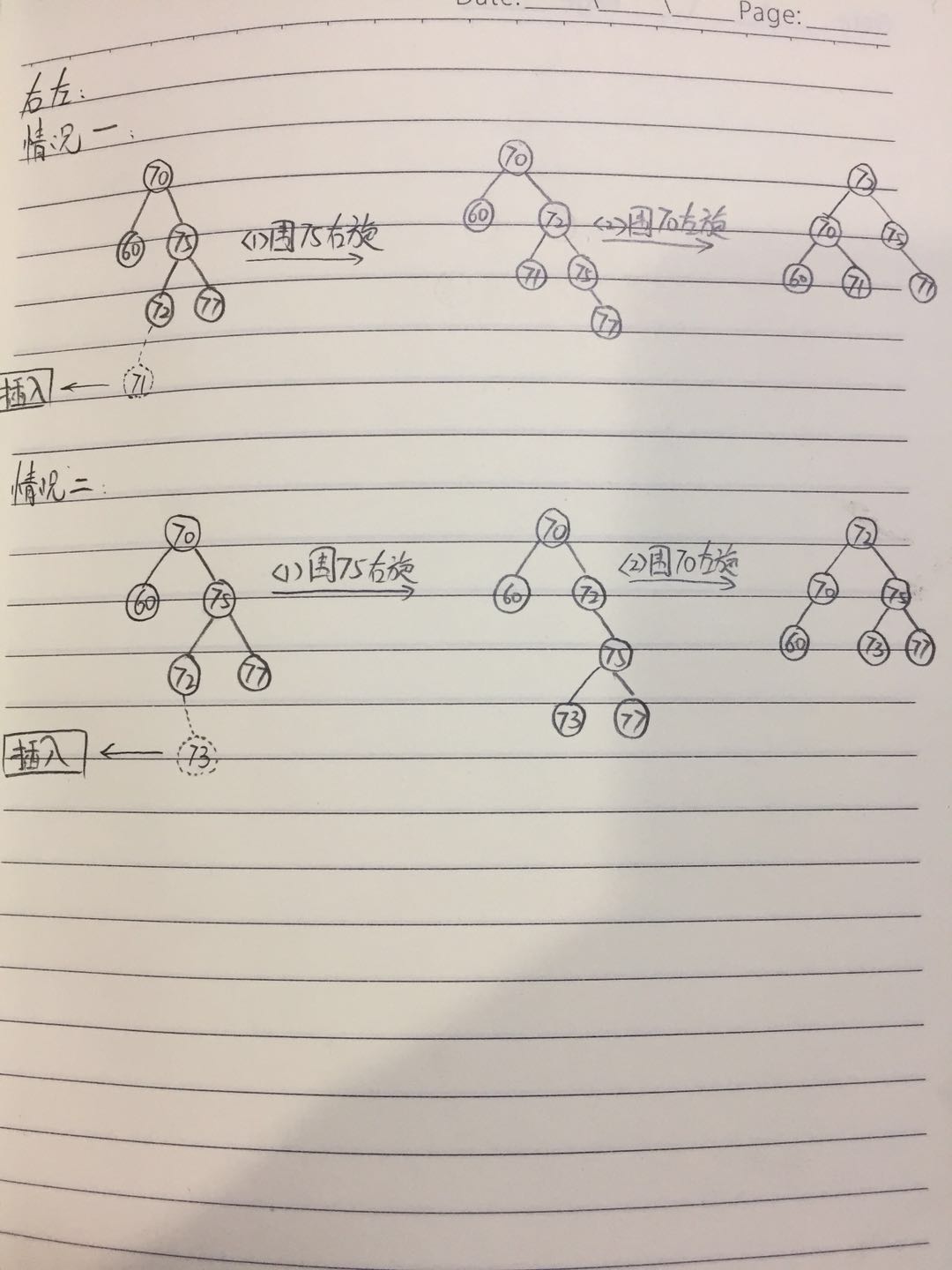
先右旋右子节点，再左旋：

//先右旋右节点，再左旋节点
node.right = rightRotate(node.right);
return leftRotate(node);

出入数据的完整实现:

public class AvlTree {

    static class TreeNode {

        /**
         * 树节点的值
         */
        private int val;

        /**
         * 树的高度
         */
        private int height;

        /**
         * 左子节点
         */
        private TreeNode left;

        /**
         * 右子节点
         */
        private TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }

    }

    /**
     * 插入节点key到以node为根的树中
     *
     * @param node
     * @param key
     * @return
     */
    public TreeNode add(TreeNode node, int key) {
        //1.插入节点:
        if (node == null)
            return new TreeNode(key);
        if (key < node.val) {
            //查找左树
            node.left = add(node.left, key);
        } else if (key > node.val) {
            //查找右树
            node.right = add(node.right, key);
        } else {
            //do noting
            return node;
        }
        //2.插入后更新节点的高度
        node.height = max(height(node.left), height(node.right));
        //3.获取平衡因子，如有失衡者，则平衡树节点
        int factor = getBalanceFactor(node);
        if (factor > 1) {
            //左高
            if (key < node.left.val) {
                //只右旋转一次
                return rightRotate(node);
            } else {
                //先左旋左节点，再右旋节点
                node.left = leftRotate(node.left);
                return rightRotate(node);
            }
        } else if (factor < -1) {
            //右高
            if (key > node.right.val) {
                //只右旋转一次
                return leftRotate(node);
            } else {
                //先右旋右节点，再左旋节点
                node.right = rightRotate(node.right);
                return leftRotate(node);
            }
        }
        return node;
    }

    /**
     * 获取节点的平衡因子
     *
     * @param node
     * @return
     */
    private int getBalanceFactor(TreeNode node) {
        return node == null ? -1 : height(node.left) - height(node.right);
    }

    public static void main(String[] args) {
        AvlTree tree = new AvlTree();
        TreeNode node = null;
        int[] a = {3, 2, 1, 4, 5, 6, 7, 10, 9, 8};
        for (int b : a) {
            node = tree.add(node, b);
        }
        //遍历node
        inOrder(node);
        preOrder(node);
        //layerOrder(node);
    }

    /**
     * 获取节点的高度
     *
     * @param node
     * @return
     */
    private int height(TreeNode node) {
        return node == null ? -1 : max(height(node.left), height(node.right)) + 1;
    }

    /**
     * 获取二者中较大的
     *
     * @param a
     * @param b
     * @return
     */
    private int max(int a, int b) {
        return a >= b ? a : b;
    }

    /**
     * 右旋
     *
     * @param tree 待旋转的节点
     */
    private TreeNode rightRotate(TreeNode tree) {
        //拷贝源节点的左节点
        TreeNode node = tree.left;
        tree.left = node.right;
        node.right = tree;
        //重新计算节点的高度
        node.height = height(node);
//        tree.height = height(tree);
        tree = null; //help gc
        return node;
    }

    /**
     * 左旋
     *
     * @param tree 待旋转的节点
     */
    private TreeNode leftRotate(TreeNode tree) {
        TreeNode node = tree.right;
        tree.right = node.left;
        node.left = tree;
        //重新计算节点的高度
        node.height = height(node);
//        tree.height = height(tree);
        tree = null; //help gc
        return node;
    }

    /**
     * 中序遍历测试
     *
     * @param node
     */
    private static void inOrder(TreeNode node) {
        if (node != null) {
            inOrder(node.left);
            System.err.println(node.val);
            inOrder(node.right);
        }
    }

    /**
     * 前序遍历测试
     *
     * @param node
     */
    private static void preOrder(TreeNode node) {
        if (node != null) {
            System.err.println(node.val + " - height:" + node.height);
            preOrder(node.left);
            preOrder(node.right);
        }
    }
　　
    private static void layerOrder(TreeNode root) {
        Queue<TreeNode> queue = new ArrayDeque<>();
        if (root != null) queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.println(node.val);
            if (node.left != null) queue.offer(node.left);
            if (node.right != null) queue.offer(node.right);
        }
    }
}