Luogu P1187 3D模型

题目描述

一座城市建立在规则的n×m网格上，并且网格均由1×1正方形构成。在每个网格上都可以有一个建筑，建筑由若干个1×1×1的立方体搭建而成（也就是所有建筑的底部都在同一平面上的）。几个典型的城市模型如下图所示：

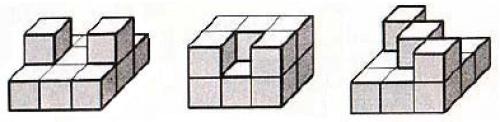
现在给出每个网格上建筑的高度，即每个网格上建筑由多少个立方体搭建而成，要求这个建筑模型的表面积是多少。

输入输出格式

输入格式：

输入文件的第1行包含2个正整数n和m，为城市模型的长与宽。

接下来n行，每行m个数字字符，描述了网格每个格子高度（可见所有建筑高度都大等于0且小等于9）。

输出格式：

输出文件包含一个非负整数，为城市模型的表面积。

输入输出样例

输入样例#1：

3 3
111
212
111

输出样例#1：

38

输入样例#2：

3 4
1000
0010
0000

输出样例#2：

12

说明

本题有2个测试数据

20%的数据满足：n, m≤10；

40%的数据满足：n, m≤100；

100%的数据满足：n, m≤1000。

---

看到许多很牛逼的题解，但都很麻烦，不如我们来换一种思路。

开一个三维数组（因为测试数据很小，高度都小于等于9）。

然后按照输入，在三位数组里标记这个点是否存在方块。

最后每个方块的六个面都判断一下，有几个面是裸露在外的（这个面没有与另一个方块相连）。那么面积就要加上一。

到最后输出面积。完成。

代码hhh

#include<cstdio>
#include<iostream>
#include<cstring>

using namespace std;

int a[1003][1003][12];
char b[1003][1003];
int n,m,sum=0;

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=m;j++) {
            cin>>b[i][j];
            b[i][j]-='0';
            for(int k=1;k<=b[i][j];k++) {
                a[i][j][k]=1;
            }
        }
    }
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=m;j++) {
            for(int k=1;k<=b[i][j];k++) {
                if(a[i][j+1][k]==0)sum++;
                if(a[i][j-1][k]==0)sum++;
                if(a[i+1][j][k]==0)sum++;
                if(a[i-1][j][k]==0)sum++;
                if(a[i][j][k+1]==0)sum++;
                if(a[i][j][k-1]==0)sum++;
            }
        }
    }
    cout<<sum;
}

作者：wlz

出处：http://www.cnblogs.com/bljfy/p/8728003.html

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。