BZOJ2142: 礼物（拓展lucas）

Description

一年一度的圣诞节快要来到了。每年的圣诞节小E都会收到许多礼物，当然他也会送出许多礼物。不同的人物在小E

心目中的重要性不同，在小E心中分量越重的人，收到的礼物会越多。小E从商店中购买了n件礼物，打算送给m个人

，其中送给第i个人礼物数量为wi。请你帮忙计算出送礼物的方案数（两个方案被认为是不同的，当且仅当存在某

个人在这两种方案中收到的礼物不同）。由于方案数可能会很大，你只需要输出模P后的结果。

Input

输入的第一行包含一个正整数P，表示模；

第二行包含两个整整数n和m，分别表示小E从商店购买的礼物数和接受礼物的人数；

以下m行每行仅包含一个正整数wi，表示小E要送给第i个人的礼物数量。

Output

若不存在可行方案，则输出“Impossible”，否则输出一个整数，表示模P后的方案数。

Sample Input

100
4 2
1
2

Sample Output

解题思路：

这道题就是组合数取模终极版。

很显然要求的就是：

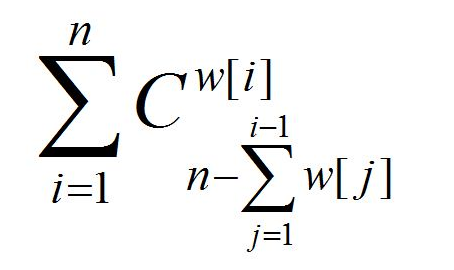
数据范围好像不是很大。

拓展lucas没跑了。

大概思路就是：先将取模数拆分，求出各部分的解，使用中国剩余定理合并答案。

中国剩余定理我就不说了。

这里主要讲一下拓展lucas。

将组合数展开：

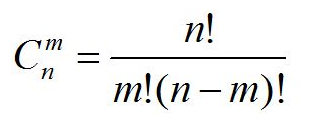
这里主要有两个问题需要解决

1.n 太大，一锅煮不下，直接枚举会超时。

2.n 比取模数大时会变成0下面本来有抵消的都没了。

我们一个一个看。

怎么计算n!呢？

我们暴力吧。

我们先看第二个吧。

先说第二个。

既然是抵消了，那么为何不让它先约掉呢。

很显然，将最小质因数p的幂次项提取出就可以完成任务。

也就是说，在处理阶乘时，跳过幂次项。

就是将原式化简成这样：

就解决了。

回来看第一个。

既然要跳过p的次幂，那么就都提出来发现剩余项是前p^k以内的数的次幂。

提出来的项可以递归操作。

差不多就是这样了。

我也不知道这和lucas有啥关系

代码：

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<algorithm>
  4 typedef long long lnt;
  5 lnt prime[100000];
  6 lnt picie[100000];
  7 lnt tmp[100000];
  8 lnt w[100000];
  9 lnt n,m;
 10 int cnt;
 11 lnt qucp(lnt a,lnt b,lnt c)
 12 {
 13     lnt ans=1;
 14     while(b)
 15     {
 16         if(b&1)
 17             ans=ans*a%c;
 18         a=a*a%c;
 19         b=b/2;
 20     }
 21     return ans%c;
 22 }
 23 void exgcd(lnt a,lnt b,lnt &x,lnt &y)
 24 {
 25     if(!b)
 26     {
 27         x=1;
 28         y=0;
 29         return ;
 30     }
 31     exgcd(b,a%b,y,x);
 32     y-=a/b*x;
 33     return ;
 34 }
 35 lnt Inv(lnt x,lnt mod)
 36 {
 37     lnt a;
 38     lnt b;
 39     exgcd(x,mod,a,b);
 40     return (a%mod+mod)%mod;
 41 }
 42 lnt Crt(lnt num,lnt *ans,lnt *mod)
 43 {
 44     lnt ret=0;
 45     lnt mdl=1;
 46     for(int i=1;i<=num;i++)
 47         mdl*=mod[i];
 48     for(int i=1;i<=num;i++)
 49     {
 50         lnt x=mdl/mod[i];
 51         ret=(ret+x*Inv(x,mod[i])%mdl*ans[i]%mdl)%mdl;
 52     }
 53     return ret;
 54 }
 55 lnt fac(lnt len,lnt pi,lnt pk)
 56 {
 57     if(!len)
 58         return 1;
 59     lnt ans=1;
 60     for(int i=2;i<=pk;i++)
 61         if(i%pi)
 62             ans=ans*i%pk;
 63     ans=qucp(ans,len/pk,pk);
 64     for(int i=2;i<=len%pk;i++)
 65         if(i%pi)
 66             ans=ans*i%pk;
 67     return ans*fac(len/pi,pi,pk)%pk;            
 68 }
 69 lnt Exlucas(lnt n,lnt m,lnt plc)
 70 {
 71     if(m>n)
 72         return 0;
 73     lnt fan=fac(n,prime[plc],picie[plc]);
 74     lnt fam=fac(m,prime[plc],picie[plc]);
 75     lnt fad=fac(n-m,prime[plc],picie[plc]);
 76     lnt ans=fan*Inv(fam,picie[plc])%picie[plc]*Inv(fad,picie[plc])%picie[plc];
 77     lnt c=0;
 78     for(int i=n;i;i/=prime[plc])
 79         c+=i/prime[plc];
 80     for(int i=m;i;i/=prime[plc])
 81         c-=i/prime[plc];
 82     for(int i=n-m;i;i/=prime[plc])
 83         c-=i/prime[plc];
 84     return ans*qucp(prime[plc],c,picie[plc])%picie[plc];
 85 }
 86 void brkdn(lnt P)
 87 {
 88     for(int i=2;i*i<=P;i++)
 89     {
 90         if(P%i==0)
 91         {
 92             cnt++;
 93             prime[cnt]=i;
 94             picie[cnt]=1;
 95             while(P%i==0)
 96             {
 97                 picie[cnt]*=(lnt)(i);
 98                 P/=i;
 99             }
100         }
101     }
102     if(P!=1)
103     {
104         cnt++;
105         picie[cnt]=prime[cnt]=P;
106     }
107     return ;
108 }
109 int main()
110 {
111     lnt Mod;
112     scanf("%lld",&Mod);
113     brkdn(Mod);
114     scanf("%lld%lld",&n,&m);
115     lnt sum=0;
116     lnt ans=1;
117     for(int i=1;i<=m;i++)
118     {
119         scanf("%lld",&w[i]);
120         sum+=w[i];
121     }
122     if(sum>n)
123     {
124         puts("Impossible");
125         return 0;
126     }
127     for(int i=1;i<=m;i++)
128     {
129         for(int j=1;j<=cnt;j++)
130             tmp[j]=Exlucas(n,w[i],j);
131         ans=ans*Crt(cnt,tmp,picie)%Mod;
132         n-=w[i];
133     }
134     printf("%lld
",ans);
135     return 0;
136 }