题目描述
1920年的芝加哥,出现了一群强盗。如果两个强盗遇上了,那么他们要么是朋友,要么是敌人。而且有一点是肯定的,就是:
我朋友的朋友是我的朋友;
我敌人的敌人也是我的朋友。
两个强盗是同一团伙的条件是当且仅当他们是朋友。现在给你一些关于强盗们的信息,问你最多有多少个强盗团伙。
输入输出格式
输入格式:输入文件gangs.in的第一行是一个整数N(2<=N<=1000),表示强盗的个数(从1编号到N)。 第二行M(1<=M<=5000),表示关于强盗的信息条数。 以下M行,每行可能是F p q或是E p q(1<=p q<=N),F表示p和q是朋友,E表示p和q是敌人。输入数据保证不会产生信息的矛盾。
输出格式:输出文件gangs.out只有一行,表示最大可能的团伙数。
输入输出样例
输入样例#1:
6 4 E 1 4 F 3 5 F 4 6 E 1 2
输出样例#1:
3
思路
题目的数据比较水。。。。
要注意的有比如,可能不是朋友也不是敌人啊QwQ
然后的话,朋友肯定是一个集合的啦,那么敌人的话呢?
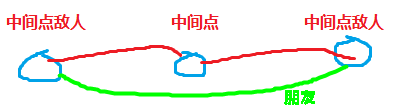
因为深受上次在JZ时小X的最短路的洗脑,于是有了对Floyd的各种奇奇怪怪的用法,
就是说我们每次读入一对敌人a和b,
那么以a作为中间点,那么他的所有敌人肯定就是一个朋友集合啊,那就把b加到这个朋友集合里面;
然后以b作为中间点,同上原理。【刚开始这里手残打错了。。。】
统计的时候只要统计father[k]=k的个数就可以了
Codes
1 program group; 2 const 3 inf='group.in'; 4 outf='group.out'; 5 var 6 father:array[0..1000] of longint; 7 aa:array[1..1000] of longint; //aa[i]表示i的敌人集合 ,就是i所在的集合的补集 8 ch:array[1..1000] of boolean; 9 i,n,m,a,b,t1,t2,total,k,t,j:longint; 10 p:char; 11 12 function find(apple:longint):longint; 13 begin 14 if father[apple]<>apple then father[apple]:=find(father[apple]); 15 exit(father[apple]); 16 end; 17 18 procedure union(a,b:longint); 19 begin 20 t1:=find(a); 21 t2:=find(b); 22 if t1<>t2 then father[t2]:=t1; 23 end; 24 25 begin 26 //assign(input,inf); 27 //assign(output,outf); 28 //reset(input); rewrite(output); 29 30 readln(n); readln(m); 31 for i:= 1 to n do 32 father[i]:=i; 33 34 for i:= 1 to m do 35 begin 36 readln(p,a,b); 37 if p='E' then begin 38 if aa[a]=0 then aa[a]:=b 39 else union(b,aa[a]); 40 if aa[b]=0 then aa[b]:=a 41 else union(a,aa[b]); 42 end 43 else union(a,b); 44 end; 45 46 for k:= 1 to n do 47 if k=father[k] then inc(total); 48 49 writeln(total); 50 51 close(input); 52 close(output); 53 end.
下面是刚开始的版本,略逊与上面,因为每次都和敌人集合每一个合并了,白白浪费了时间【逃】
1 program group; 2 const 3 inf='group.in'; 4 outf='group.out'; 5 var 6 father:array[0..1000] of longint; 7 aa:array[1..1000,0..1000] of longint; 8 ch:array[1..1000] of boolean; 9 i,n,m,a,b,t1,t2,total,k,t,j,y:longint; 10 st:string; 11 p:char; 12 13 function find(apple:longint):longint; 14 begin 15 if father[apple]<>apple then father[apple]:=find(father[apple]); 16 exit(father[apple]); 17 end; 18 19 procedure union(a,b:longint); 20 begin 21 t1:=find(a); 22 t2:=find(b); 23 if t1<>t2 then father[t2]:=t1; 24 end; 25 26 begin 27 // assign(input,inf); 28 // assign(output,outf); 29 // reset(input); rewrite(output); 30 31 readln(n); readln(m); 32 for i:= 1 to n do 33 father[i]:=i; 34 35 for i:= 1 to m do 36 begin 37 readln(st); 38 p:=st[1]; 39 st:=copy(st,3,n-2); 40 y:=pos(' ',st); 41 val(copy(st,1,y-1),a); 42 val(copy(st,y+1,n-y),b); 43 44 if p='E' then begin 45 for j:= 1 to aa[a,0] do 46 union(b,aa[a,j]); 47 for j:= 1 to aa[b,0] do 48 union(a,aa[b,j]); 49 inc(aa[a,0]); aa[a,aa[a,0]]:=b; 50 inc(aa[b,0]); aa[b,aa[b,0]]:=a; 51 continue; 52 end 53 else union(a,b); 54 end; 55 56 for k:= 1 to n do 57 if k=father[k] then inc(total); 58 59 writeln(total); 60 61 close(input); 62 close(output); 63 end.