KL散度(KL divergence)
全称:Kullback-Leibler Divergence。
用途:比较两个概率分布的接近程度。
在统计应用中,我们经常需要用一个简单的,近似的概率分布 f * 来描述。
观察数据 D 或者另一个复杂的概率分布 f 。这个时候,我们需要一个量来衡量我们选择的近似分布 f * 相比原分布 f 究竟损失了多少信息量,这就是KL散度起作用的地方。
熵(entropy)
想要考察信息量的损失,就要先确定一个描述信息量的量纲。
在信息论这门学科中,一个很重要的目标就是量化描述数据中含有多少信息。
为此,提出了熵的概念,记作 H 。
一个概率分布所对应的熵表达如下: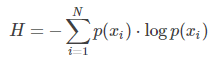
如果我们使用 log 2 作为底,熵可以被理解为:我们编码所有信息所需要的最小位数(minimum numbers of bits)。
需要注意的是:通过计算熵,我们可以知道信息编码需要的最小位数,却不能确定最佳的数据压缩策略。怎样选择最优数据压缩策略,使得数据存储位数与熵计算的位数相同,达到最优压缩,是另一个庞大的课题。
KL散度的计算
现在,我们能够量化数据中的信息量了,就可以来衡量近似分布带来的信息损失了。
KL散度的计算公式其实是熵计算公式的简单变形,在原有概率分布 p 上,加入我们的近似概率分布 q ,计算他们的每个取值对应对数的差:
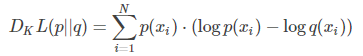
换句话说,KL散度计算的就是数据的原分布与近似分布的概率的对数差的期望值。
在对数以2为底时, log 2 ,可以理解为“我们损失了多少位的信息”。
写成期望形式:
更常见的是以下形式: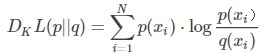
现在,我们就可以使用KL散度衡量我们选择的近似分布与数据原分布有多大差异了。
散度不是距离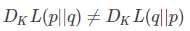
因为KL散度不具有交换性,所以不能理解为“距离”的概念,衡量的并不是两个分布在空间中的远近,更准确的理解还是衡量一个分布相比另一个分布的信息损失(infomation lost)。
使用KL散度进行优化
通过不断改变预估分布的参数,我们可以得到不同的KL散度的值。
在某个变化范围内,KL散度取到最小值的时候,对应的参数是我们想要的最优参数。
这就是使用KL散度优化的过程。
神经网络进行的工作很大程度上就是“函数的近似”(function approximators)。
因此我们可以使用神经网络学习很多复杂函数,学习过程的关键就是设定一个目标函数来衡量学习效果。
也就是通过最小化目标函数的损失来训练网络(minimizing the loss of the objective function)。
而KL散度可以作为正则化项(regularization term)加入损失函数之中,即使用KL散度来最小化我们近似分布时的信息损失,让我们的网络可以学习很多复杂的分布。
一个典型应用是VAE(变分自动编码)。