POJ_1330 Nearest Common Ancestors LCA

题目链接：http://poj.org/problem?id=1330

最近公共祖先模板题

Tarjan离线算法 ：

读取所有询问后保存并按照一定方式排列。该算法主要采取深度优先搜索的方式，结合并查集，在搜索同时处理查询，大致过程如下：

搜索到节点u

　　访问标记u

　　对于u的所有子节点递归搜索，每搜索并处理完一个子节点后将其与当前节点合并，u为父节点

　　若有一个与u关联的询问 q(u, v) 并且 v 已经被访问过，则其lca为 find(v) - 即并查集父节点函数

为何lca为 find(v) :

如果有一个从当前结点到结点v的询问，且v已被检查过，则由于进行的是深度优先搜索，当前结点与v的最近公共祖先一定还没有被检查，而这个最近公共祖先的包涵v的子树一定已经搜索过了，那么这个最近公共祖先一定是v所在集合的祖先。

参考：http://dongxicheng.org/structure/lca-rmq/

实际代码编写中需要注意初始化，并查集合并时父节点是否一定等问题，细节处理要谨慎。

伪代码：

lca(node u){
    fa[u] = u;
    vis[u] = 1;
    for every son of u{
        lca(u.son)
        union(u, u.son);
    }
    for every query of u {
        if vis[q[u]] == 1
            ans[u].push_back(find(q[u]))
    }
}

题目AC代码：

const int inf = 0x3f3f3f3f;
const int maxn = 1e4 + 5;
struct Edge{
    int to, next, val;
}; 
Edge edges[maxn * 2];
int tot, head[maxn], vis[maxn];
int n;
int fa[maxn];
int qu, qv, ans;
int deg[maxn];

void init(){
    memset(deg, 0, sizeof(deg));
    memset(edges, 0, sizeof(edges));
    memset(head, -1, sizeof(head));
    memset(vis, 0, sizeof(vis));
    for(int i = 0; i <= n; i++) fa[i] = i;
    tot = 0;
}
void addEdge(int u, int v, int w){
    edges[tot].to = v;
    edges[tot].val = w;
    edges[tot].next = head[u];
    head[u] = tot++;
}

int find(int x){
    return (fa[x] == x)? x: fa[x] = find(fa[x]);
}
void unite(int x, int y){
    int fx = find(x), fy = find(y);
    if(fx == fy) return;
    fa[fy] = fx;
}

void lca(int u){
    fa[u] = u;
    vis[u] = 1;
    for(int i = head[u]; i != -1; i = edges[i].next){
        if(!vis[edges[i].to]) {
            lca(edges[i].to);
            unite(u, edges[i].to);
        }
    }
    if(u == qu && vis[qv] == 1){
        ans = find(qv);
    }
    if(u == qv && vis[qu] == 1){
        ans = find(qu);
    }
}


int main(){
    int T;
    scanf("%d", &T);
    while(T--){
        scanf("%d", &n);
        init();
        for(int i = 0; i < n - 1; i++){
            int from, to;
            scanf("%d %d", &from, &to);
            deg[to]++;
            addEdge(from, to, 1);
            addEdge(to, from, 1);
        }
        int root = 1;
        for(int i = 1; i <= n; i++) if(deg[i] == 0) root = i;
        scanf("%d %d", &qu, &qv);
        lca(root);
        printf("%d
", ans);
    }
}

题目：

earest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 29509		Accepted: 15069

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below: 

 
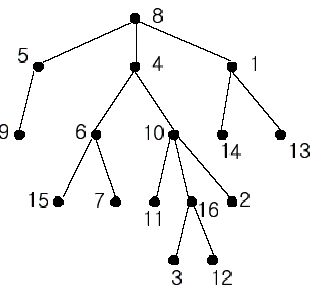
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is. 

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y. 

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3