CF Round 432 C. Five Dimensional Points

题目链接：http://codeforces.com/contest/851/problem/C

题目大意：给出N个点，判断有多少个点是good的。对于一个点a来说，如果能从给出的N个点钟找到两个与a不同的点b，c并且 向量 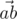 和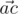夹角是锐角，则说这个点是bad的，否则是good的。N < 1000

解题思路：首先会想到的是N³的算法，但是仔细考虑一下会发现，如果a是bad的，那么一次判断即可，否则a是good，那么b，c肯定都是bad。那么复杂度就可以大大降低了。

代码：

const int maxn = 1e3 + 5;
int n;
int a[maxn], b[maxn], c[maxn], d[maxn], e[maxn];
bool sta[maxn];
queue<int> q;

double cacu(int ab[], int ac[]){
    double ans = 0;
    for(int i = 0; i < 5; i++){
        ans += ab[i] * ac[i];
    } 
    return ans;
}
void solve(){
    memset(sta, 0, sizeof(sta));
    int ans = 0;
    for(int i = 1; i <= n; i++){
        if(!sta[i]){
            bool flag = true;
            sta[i] = true;
            for(int j = 1; j <= n; j++){
                if(j == i) continue;
                for(int k = 1; k <= n; k++){
                    if(k == i || k == j) continue;
                    int ab[] = {a[j] - a[i], b[j] - b[i], c[j] - c[i], d[j] - d[i], e[j] - e[i]};
                    int ac[] = {a[k] - a[i], b[k] - b[i], c[k] - c[i], d[k] - d[i], e[k] - e[i]};
                    double tv1 = cacu(ab, ac), tv2 = cacu(ab, ab), tv3 = cacu(ac, ac);
                    double tmv = tv1 / sqrt(tv2) / sqrt(tv3);
                    tmv = acos(tmv);
                    if(tmv - PI / 2 < 0){
                        flag = false;
                        break;
                    }
                    else{
                        sta[j] = sta[k] = true;
                    }
                }
                if(!flag) break;
            }
            if(flag) {
                ans++;
                q.push(i);
            }
        }
    }
    printf("%d
", ans);
    while(!q.empty()){
        int u = q.front(); q.pop();
        printf("%d ", u);
    }
}
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%d %d %d %d %d", a + i, b + i, c + i, d + i, e + i);
    }
    solve();
}

题目：

C. Five Dimensional Points

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given set of n points in 5-dimensional space. The points are labeled from 1 to n. No two points coincide.

We will call point a bad if there are different points b and c, not equal to a, from the given set such that angle between vectors 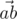 and 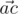is acute (i.e. strictly less than 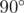). Otherwise, the point is called good.

The angle between vectors 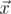 and 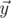 in 5-dimensional space is defined as 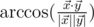, where  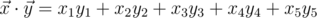is the scalar product and  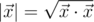is length of .

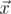Given the list of points, print the indices of the good points in ascending order.

Input

The first line of input contains a single integer n (1 ≤ n ≤ 103) — the number of points.

The next n lines of input contain five integers ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103)  — the coordinates of the i-th point. All points are distinct.

Output

First, print a single integer k — the number of good points.

Then, print k integers, each on their own line — the indices of the good points in ascending order.

Examples

input

6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1

output

1
1

input

3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0

output

0

Note

In the first sample, the first point forms exactly a 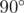 angle with all other pairs of points, so it is good.

In the second sample, along the cd plane, we can see the points look as follows:

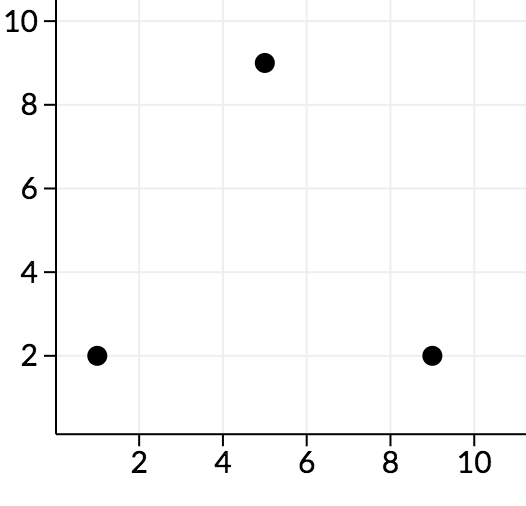
We can see that all angles here are acute, so no points are good.