区块链技术架构分析(3)-默克尔树(merkle tree)
默克尔树(Merkle
tree,MT)是一种哈希二叉树,1979年由Ralph
Merkle发明。在计算机科学中,二叉树是每个节点最多有两个子树的树结构,每个节点代表一条结构化数据。通常子树被称作“左子树”(left
subtree)和“右子树”(right subtree)。二叉树常被用于实现数据快速查询。二叉树如下图所示。
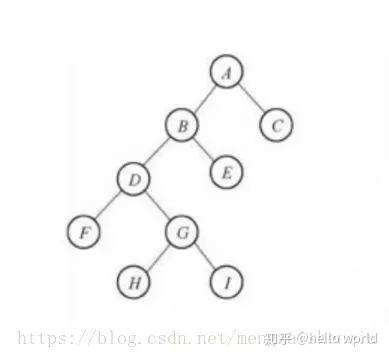
A、Merkle树结构
由一个根节点(root)、一组中间节点和一组叶节点(leaf)组成。叶节点(leaf)包含存储数据或其哈希值,中间节点是它的两个孩子节点内容的哈希值,根节点也是由它的两个子节点内容的哈希值组成。所以Merkle树也称哈希树。
B、哈希树的特点
叶节点存储的是数据文件,而非叶节点存储的是其子节点的哈希值(Hash,通过SHA1、SHA256等哈希算法计算而来),这些非叶子节点的Hash被称作路径哈希值(可以据其确定某个叶节点到根节点的路径),
叶节点的Hash值是真实数据的Hash值。因为使用了树形结构, 其查询的时间复杂度为 O(logn),n是节点数量。
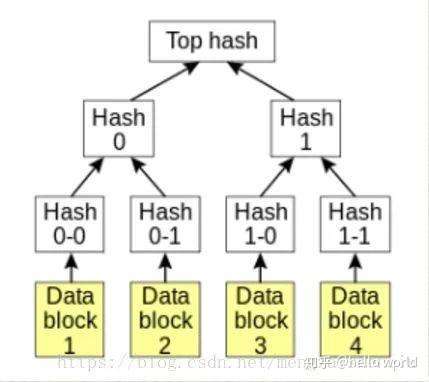
默克尔树的另一个特点是,底层数据的任何变动,都会传递到其父节点,一直到树根。
C、应用模式
默克尔树的典型应用场景包括:
l 快速比较大量数据:当两个默克尔树根相同时,则意味着所代表的数据必然相同(哈希算法决定的)。
l 快速定位修改:例如上例中,如果 D1 中数据被修改,会影响到Hash0-0,Hash0 和 Root。因此,沿着 Root --> 0 --> 0-0,可以快速定位到发生改变的 D1;
l 零知识证明:例如如何证明某个数据(D0……D3)中包括给定内容 D0,很简单,构造一个默克尔树,公布 N0,N1,N4,Root,D0拥有者可以很容易检测 D0 存在,但不知道其它内容。
相对于 Hash List,MT的明显的一个好处是可以单独拿出一个分支来(作为一个小树)对部分数据进行校验,这个很多使用场合就带来了哈希列表所不能比拟的方便和高效。正是源于这些优点,MT常用于分布式系统或分布式存储中
D、在分布式存储系统中的应用原理
为了保持数据一致,分布系统间数据需要同步,如果对机器上所有数据都进行比对的话,数据传输量就会很大,从而造成“网络拥挤”。为了解决这个问题,可以在每台机器上构造一棵Merkle
Tree,这样,在两台机器间进行数据比对时,从Merkle
Tree的根节点开始进行比对,如果根节点一样,则表示两个副本目前是一致的,不再需要任何处理;如果不一样,则沿着hash值不同的节点路径查询,很快就能定位到数据不一致的叶节点,只用把不一致的数据同步即可,这样大大节省了比对时间以及数据的传输量。
E、比特币中的Merkle Tree
比特币区块链系统中的采用的是Merkle二叉树,它的作用主要是快速归纳和校验区块数据的完整性,它会将区块链中的数据分组进行哈希运算,向上不断递归运算产生新的哈希节点,最终只剩下一个Merkle根存入区块头中,每个哈希节点总是包含两个相邻的数据块或其哈希值。
在比特币系统中使用Merkle树有诸多优点:首先是极大地提高了区块链的运行效率和可扩展性,使得区块头只需包含根哈希值而不必封装所有底层数据,这使得哈希运算可以高效地运行在智能手机甚至物联网设备上;其次是Merkle树可支持“简化支付验证协议”(SPV),即在不运行完整区块链网络节点的情况下,也能够对交易数据进行检验。所以,在区块链中使用Merkle树这种数据结构是非常具有意义的。
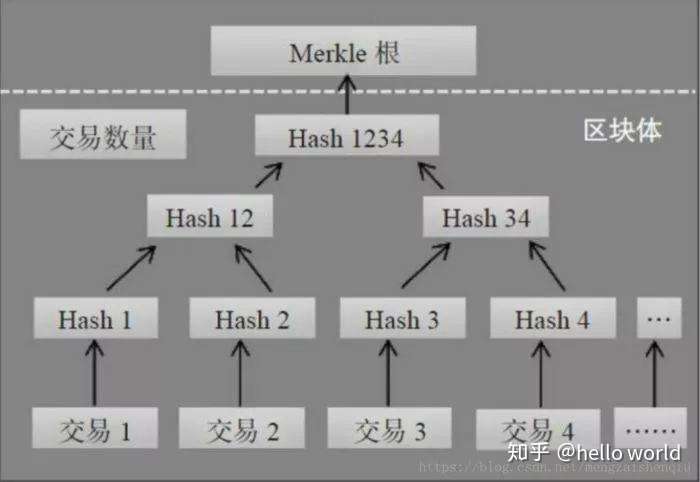
Merkle树的计算可参考:
https://www.cnblogs.com/fengzhiwu/p/5524324.html
https://blog.csdn.net/qq_33935254/article/details/55505472