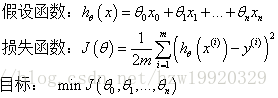线性回归的一般形式
过拟合问题及其解决方法
- 问题:以下面一张图片展示过拟合问题
- 解决方法:(1):丢弃一些对我们最终预测结果影响不大的特征,具体哪些特征需要丢弃可以通过PCA算法来实现;(2):使用正则化技术,保留所有特征,但是减少特征前面的参数θ的大小,具体就是修改线性回归中的损失函数形式即可,岭回归以及Lasso回归就是这么做的。
岭回归与Lasso回归
岭回归与Lasso回归的出现是为了解决线性回归出现的过拟合以及在通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆这两类问题的,这两种回归均通过在损失函数中引入正则化项来达到目的,具体三者的损失函数对比见下图:
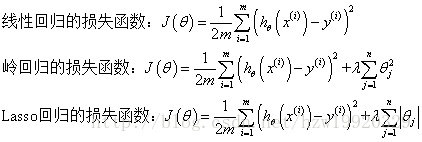
其中λ称为正则化参数,如果λ选取过大,会把所有参数θ均最小化,造成欠拟合,如果λ选取过小,会导致对过拟合问题解决不当,因此λ的选取是一个技术活。
岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项,Lasso回归引入的是L1范数惩罚项,Lasso回归能够使得损失函数中的许多θ均变成0,这点要优于岭回归,因为岭回归是要所有的θ均存在的,这样计算量Lasso回归将远远小于岭回归。
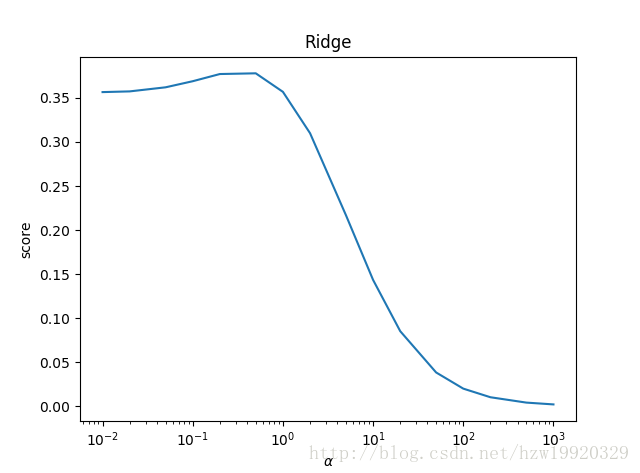
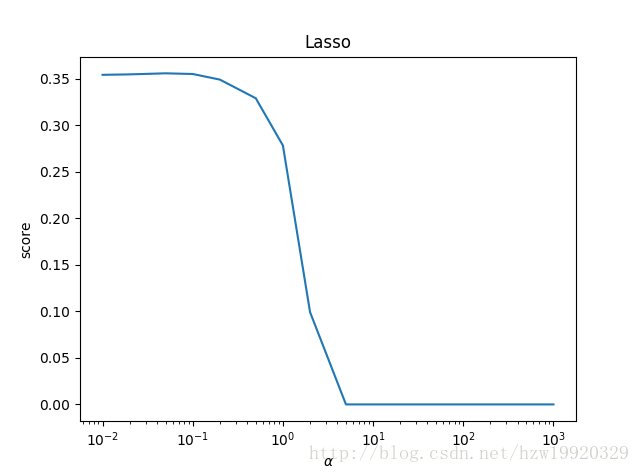
可以看到,Lasso回归最终会趋于一条直线,原因就在于好多θ值已经均为0,而岭回归却有一定平滑度,因为所有的θ值均存在。摘自:https://blog.csdn.net/hzw19920329/article/details/77200475