本文目的
最近一直在使用R进行hcluster计算,主要采用了一些R自带的距离公式和cophenetic距离验证聚类的质量。其中R自带的hclust方法不支持cosine函数,如果需要下载R的扩展,要下载许多关联的库,所以自己编写了一个简单的cosine函数,并且使用了R的proxy扩展(距离计算框架),计算向量距离。内容涉及比较多,所以记录一下,作为备忘。
采用R计算hclust
步骤一:准备数据。采用read.table函数,读取外部文件,实验文件这里下载。
cd = read.table("d:/cluster_data.txt", header = TRUE);
attributes(cd);
截图如下:
cd是一个特征举证,每一行是文档的id和此文档的特征向量,代表一个文本,列代表的是词语,这里用wN代替。
步骤二:计算文本之间的距离矩阵。距离矩阵用作度量聚类之间的相近程度。常用的距离公式有欧式距离,manhattan距离。计算方法如下:
cds = dist(cd, method="euclidean") attributes(cds)
截图如下:
步骤三:计算层级聚类。常用的聚类方式有三种,single,complete和average。
- single: 两个聚类之间最近的点作为聚类的距离
- complete:两个聚类之间最远的点作为聚类的距离
- average:将聚类中的所有向量之和的平局向量作为聚类中心点,中心点最近的聚合成一类。
averge聚类的效果介于single和complte之间,如下面命令,
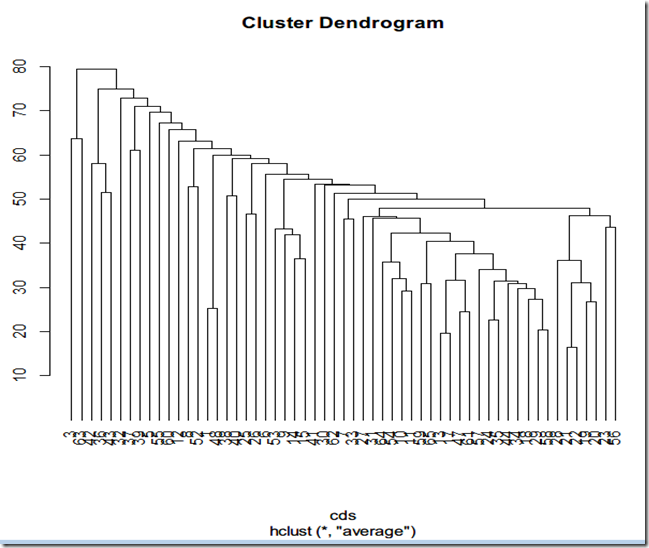
cave = hclust(cds, method="average") plot(cave,hang=-1)
下面聚类后的依赖树:
步骤四:验证聚类。层级聚类采用cophenetic distance用于度量聚类的效果(具体什么是cophenetic disctance可以参见Introduction to Data Mining by Pang-Ning Tan & Michael Steinbach & Vipin Kumar: Chapter 8.5.4)。R提供了此函数的实现,所以可以直接调用cophenetic函数验证结果,此函数值是介于-1~1之间,越大,说明聚类效果越好。命令如下,
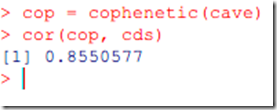
cop = cophenetic(cave) cor(cop, cds)
结果如下:
采用余弦定理cosine计算文本之间的距离
余弦定理可以计算文本向量的相似度,吴军先生的数学之美系列描述过此应用。但是,上面提到的dist方法不知此余弦公式。尝试过使用其他扩展中的相关实现,但是无法直接使用。最后找到一个解决方案,使用R扩展库proxy提供的dist计算框架,然后加入加入自己的cosine的简单实现,如果添加R扩展,可以参见这里。自定义cosine函数如下:
cosine = function(a,b) {
len = (sqrt(a %*% a)*sqrt(b %*% b));
if (len == 0) {
0;
} else {
(a %*% b)/len;
}
}
(是不是写法有点像JS)
定义好cosine后,加载proxy库,
library(proxy)
计算距离方法与上面一样,只是method的值为cosine,如下
cds = dist(t,method="cosine")
注意,一定要加引号,否则调用的是sine。计算聚类的方式与上面一样,这里不再重复。
所有距离方法和聚类方法的测试脚本
disFunc = c("euclidean", "maximum", "manhattan" , "canberra", "binary", "minkowski");
#disFunc = c("euclidean", "cosine");
cluFunc = c("complete", "single", "average", "ward", "mcquitty", "median", "centroid");
qc = read.table("d:/cluster_data.txt", header = TRUE);
for (dis in disFunc) {
for (clu in cluFunc) {
qcDis = dist(qc, method=dis);
c = hclust(qcDis, method=clu);
cop = cophenetic(c);
r = cor(cop,qcDis);
print(paste(dis, clu, r, sep=" "));
}
}
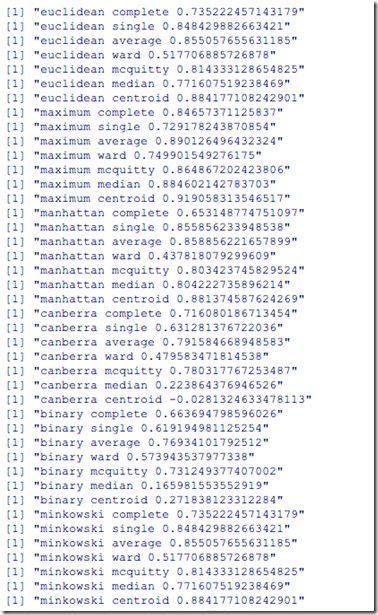
运行结果如下:
实验总结
实验过程中,发现距离公司相同的情况下,average的评测结果一般是最好的。不同距离公式的同一种聚类方式没有比较意义,比如即使euclidean的average方式比manhattan的average的验证结果低,但是并不意味前者的聚类结果比后者差,因为聚类评测都是根据统一中方法的距离公司计算相关系数,所以没有比较性。
相关资料
- proxy框架与自定义距离函数: http://stackoverflow.com/questions/7482797/how-to-specify-other-method-for-dist-function-in-r
- Cluster Analysis : Toturial with R: http://cc.oulu.fi/~jarioksa/opetus/metodi/sessio3.pdf
- Introduction to Data Mining by Pang-Ning Tan & Michael Steinbach & Vipin Kumar: Chapter 8.5.4
- 数学之美十二 余弦定理和新闻分类: http://www.google.com.hk/ggblog/googlechinablog/2006/07/12_4010.html