数据结构与算法_28 _ 堆和堆排序：为什么说堆排序没有快速排序快？

我们今天讲另外一种特殊的树，“堆”（$Heap$）。堆这种数据结构的应用场景非常多，最经典的莫过于堆排序了。堆排序是一种原地的、时间复杂度为$O(nlog n)$的排序算法。

前面我们学过快速排序，平均情况下，它的时间复杂度为$O(nlog n)$。尽管这两种排序算法的时间复杂度都是$O(nlog n)$，甚至堆排序比快速排序的时间复杂度还要稳定，但是，在实际的软件开发中，快速排序的性能要比堆排序好，这是为什么呢？

现在，你可能还无法回答，甚至对问题本身还有点疑惑。没关系，带着这个问题，我们来学习今天的内容。等你学完之后，或许就能回答出来了。

如何理解“堆”？

前面我们提到，堆是一种特殊的树。我们现在就来看看，什么样的树才是堆。我罗列了两点要求，只要满足这两点，它就是一个堆。

• 堆是一个完全二叉树；

• 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。

我分别解释一下这两点。

第一点，堆必须是一个完全二叉树。还记得我们之前讲的完全二叉树的定义吗？完全二叉树要求，除了最后一层，其他层的节点个数都是满的，最后一层的节点都靠左排列。

第二点，堆中的每个节点的值必须大于等于（或者小于等于）其子树中每个节点的值。实际上，我们还可以换一种说法，堆中每个节点的值都大于等于（或者小于等于）其左右子节点的值。这两种表述是等价的。

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做“小顶堆”。

定义解释清楚了，你来看看，下面这几个二叉树是不是堆？

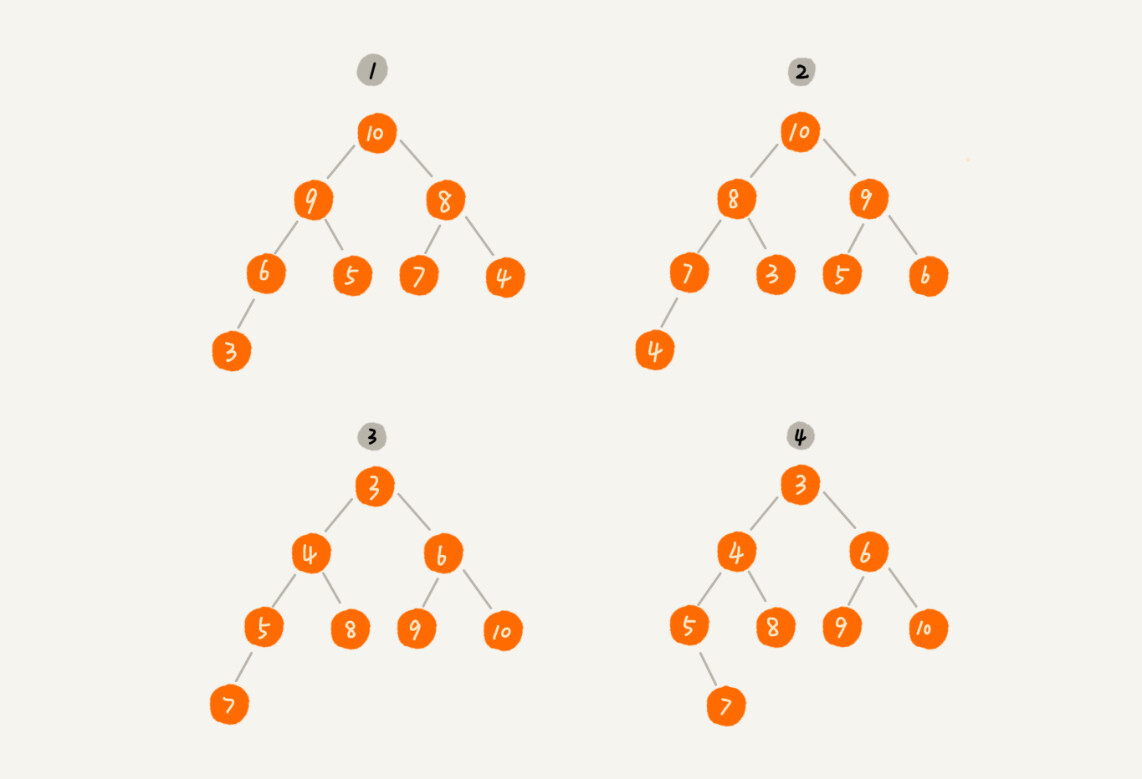
其中第$1$个和第$2$个是大顶堆，第$3$个是小顶堆，第$4$个不是堆。除此之外，从图中还可以看出来，对于同一组数据，我们可以构建多种不同形态的堆。

如何实现一个堆？

要实现一个堆，我们先要知道，堆都支持哪些操作以及如何存储一个堆。

我之前讲过，完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点。

我画了一个用数组存储堆的例子，你可以先看下。

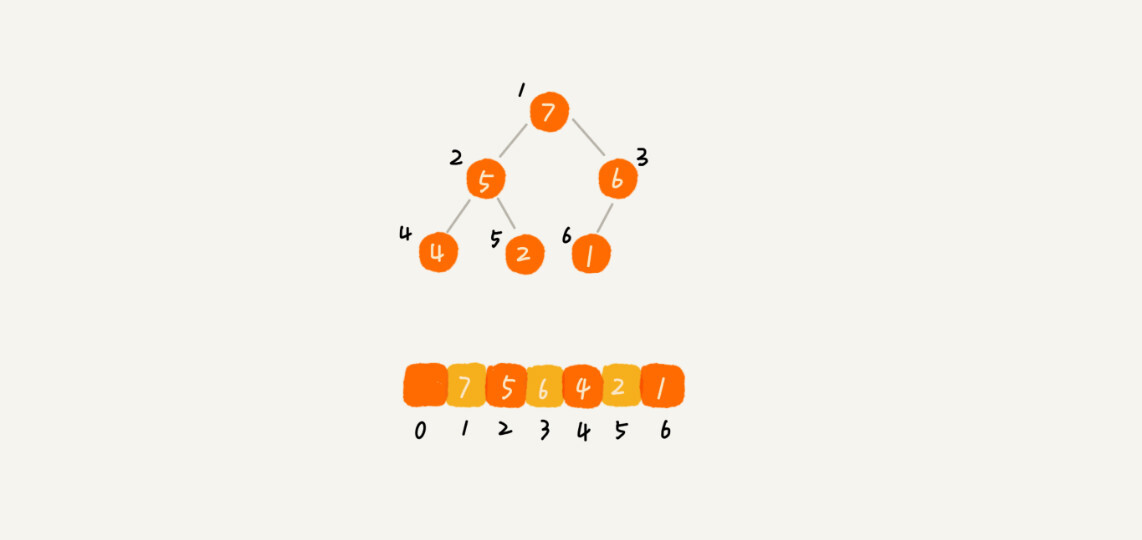
从图中我们可以看到，数组中下标为$i$的节点的左子节点，就是下标为$i*2$的节点，右子节点就是下标为$i*2+1$的节点，父节点就是下标为$frac{i}{2}$的节点。

知道了如何存储一个堆，那我们再来看看，堆上的操作有哪些呢？我罗列了几个非常核心的操作，分别是往堆中插入一个元素和删除堆顶元素。（如果没有特殊说明，我下面都是拿大顶堆来讲解）。

1.往堆中插入一个元素

往堆中插入一个元素后，我们需要继续满足堆的两个特性。

如果我们把新插入的元素放到堆的最后，你可以看我画的这个图，是不是不符合堆的特性了？于是，我们就需要进行调整，让其重新满足堆的特性，这个过程我们起了一个名字，就叫做堆化（heapify）。

堆化实际上有两种，从下往上和从上往下。这里我先讲从下往上的堆化方法。

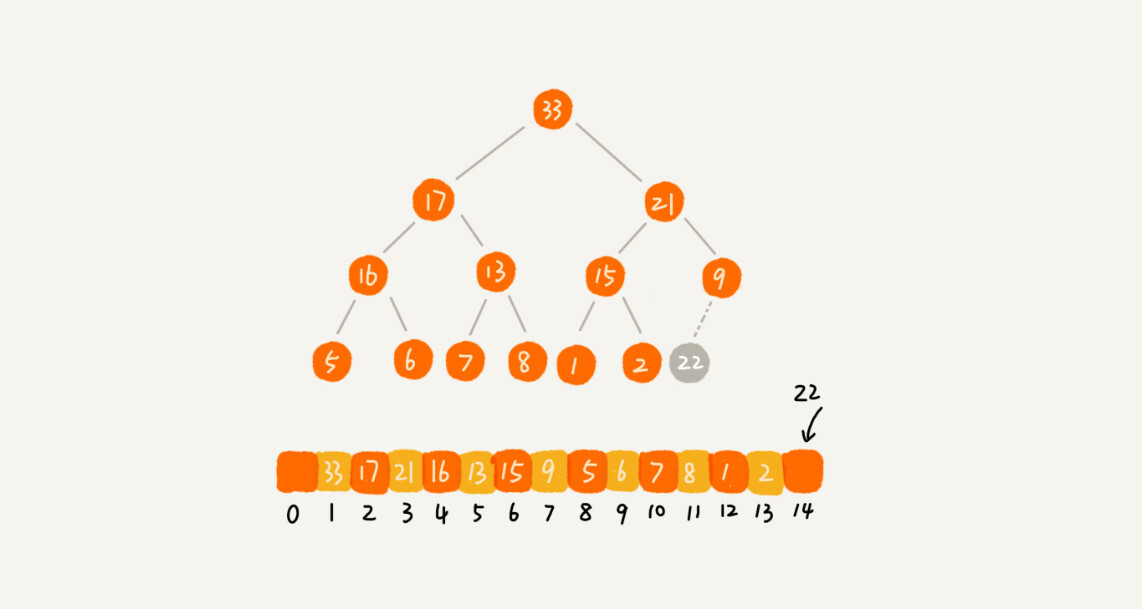
堆化非常简单，就是顺着节点所在的路径，向上或者向下，对比，然后交换。

我这里画了一张堆化的过程分解图。我们可以让新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系，我们就互换两个节点。一直重复这个过程，直到父子节点之间满足刚说的那种大小关系。

我将上面讲的往堆中插入数据的过程，翻译成了代码，你可以结合着一块看。

public class Heap {
  private int[] a; // 数组，从下标1开始存储数据
  private int n;  // 堆可以存储的最大数据个数
  private int count; // 堆中已经存储的数据个数
public Heap(int capacity) {

a = new int[capacity + 1];

n = capacity;

count = 0;

}
public void insert(int data) {

if (count >= n) return; // 堆满了

++count;

a[count] = data;

int i = count;

while (i/2 > 0 && a[i] > a[i/2]) { // 自下往上堆化

swap(a, i, i/2); // swap()函数作用：交换下标为i和i/2的两个元素

i = i/2;

}

}

}

2.删除堆顶元素

从堆的定义的第二条中，任何节点的值都大于等于（或小于等于）子树节点的值，我们可以发现，堆顶元素存储的就是堆中数据的最大值或者最小值。

假设我们构造的是大顶堆，堆顶元素就是最大的元素。当我们删除堆顶元素之后，就需要把第二大的元素放到堆顶，那第二大元素肯定会出现在左右子节点中。然后我们再迭代地删除第二大节点，以此类推，直到叶子节点被删除。

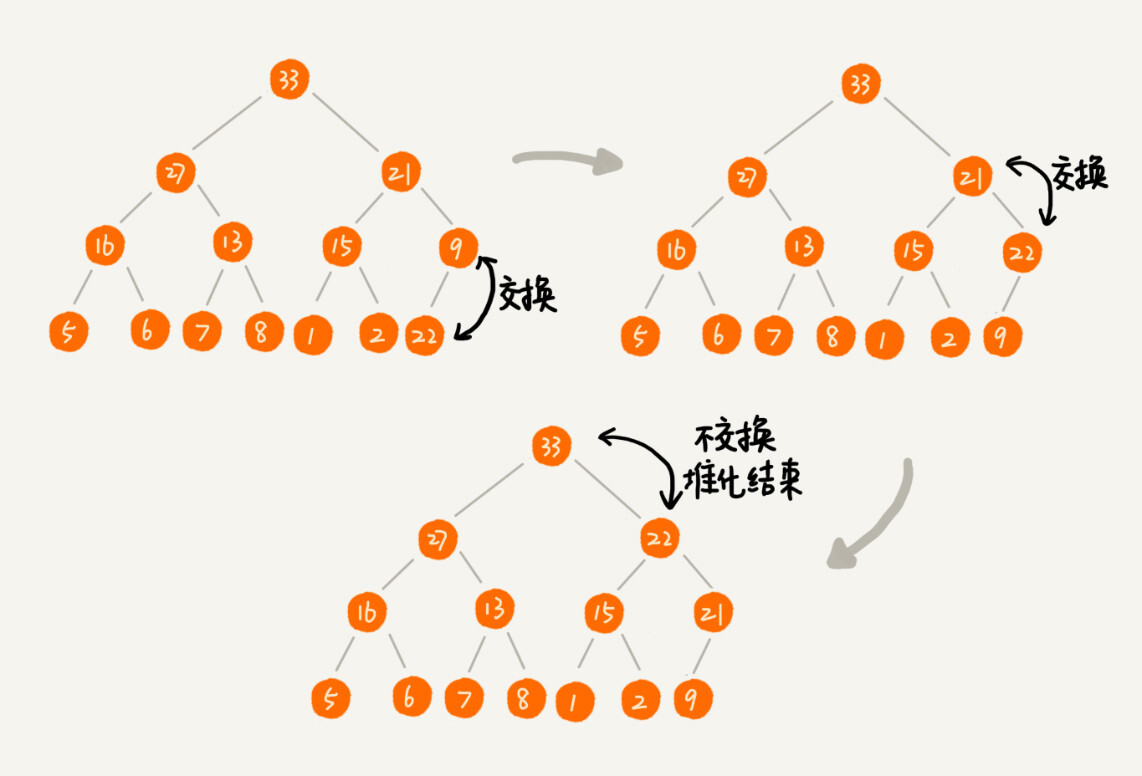
这里我也画了一个分解图。不过这种方法有点问题，就是最后堆化出来的堆并不满足完全二叉树的特性。

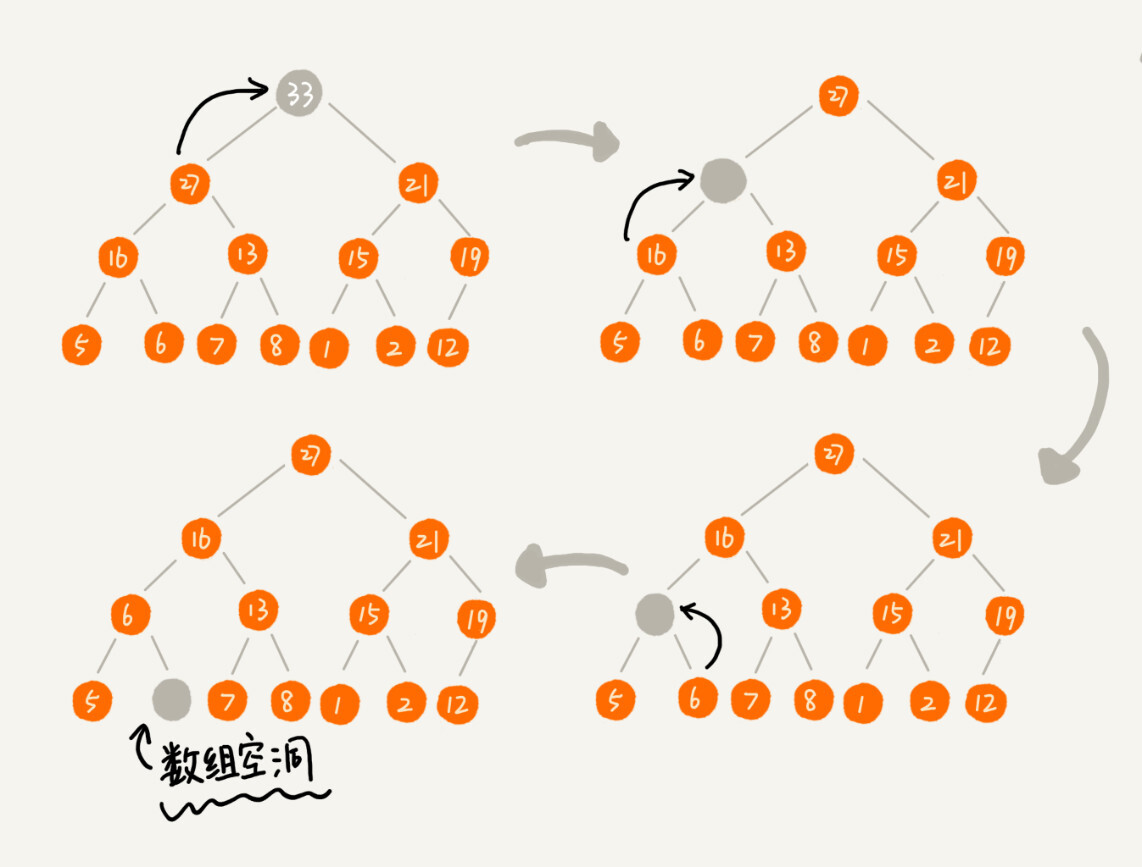
实际上，我们稍微改变一下思路，就可以解决这个问题。你看我画的下面这幅图。我们把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，并且重复进行这个过程，直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。

因为我们移除的是数组中的最后一个元素，而在堆化的过程中，都是交换操作，不会出现数组中的“空洞”，所以这种方法堆化之后的结果，肯定满足完全二叉树的特性。

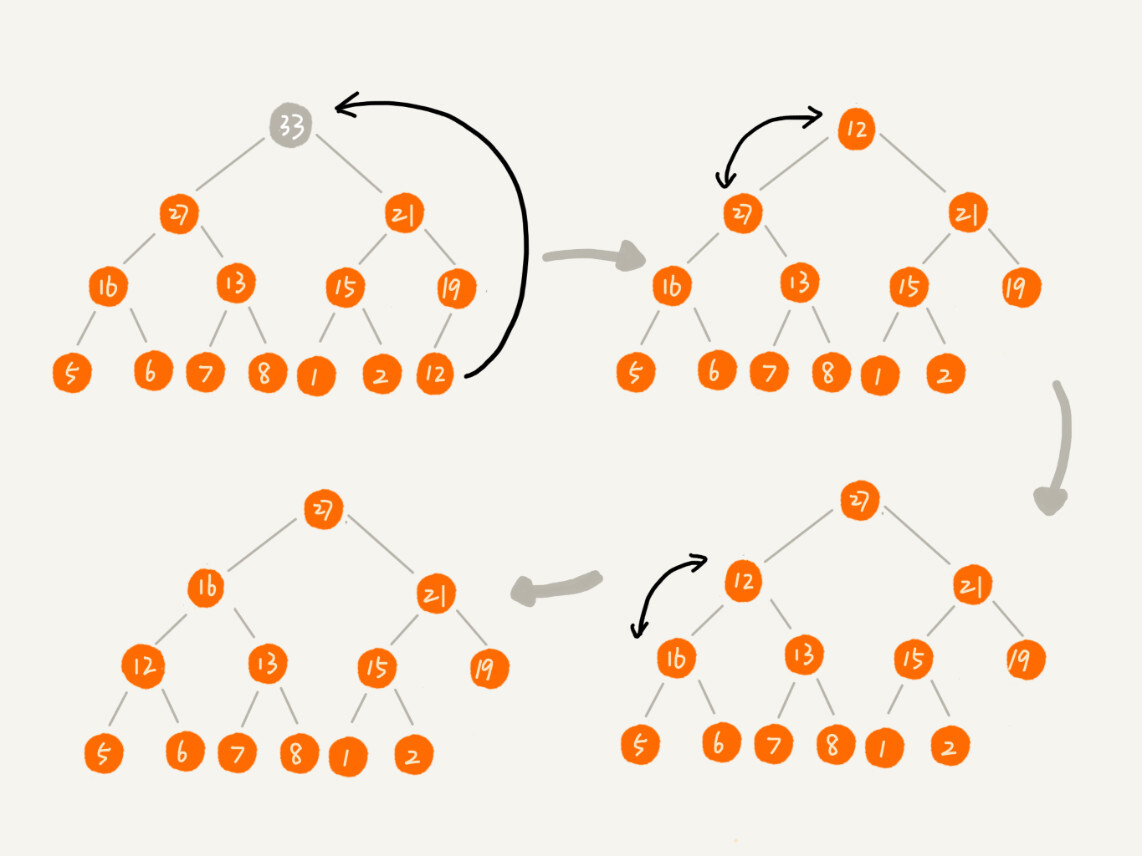
我把上面的删除过程同样也翻译成了代码，贴在这里，你可以结合着看。

public void removeMax() {

if (count == 0) return -1; // 堆中没有数据

a[1] = a[count];

--count;

heapify(a, count, 1);

}

private void heapify(int[] a, int n, int i) { // 自上往下堆化

while (true) {

int maxPos = i;

if (i2 <= n && a[i] < a[i2]) maxPos = i2;

if (i2+1 <= n && a[maxPos] < a[i2+1]) maxPos = i2+1;

if (maxPos == i) break;

swap(a, i, maxPos);

i = maxPos;

}

}

我们知道，一个包含(n)个节点的完全二叉树，树的高度不会超过(log_{2}n)。堆化的过程是顺着节点所在路径比较交换的，所以堆化的时间复杂度跟树的高度成正比，也就是(O(log n))。插入数据和删除堆顶元素的主要逻辑就是堆化，所以，往堆中插入一个元素和删除堆顶元素的时间复杂度都是(O(log n))。

如何基于堆实现排序？

前面我们讲过好几种排序算法，我们再来回忆一下，有时间复杂度是(O(n^{2}))的冒泡排序、插入排序、选择排序，有时间复杂度是(O(nlog n))的归并排序、快速排序，还有线性排序。

这里我们借助于堆这种数据结构实现的排序算法，就叫做堆排序。这种排序方法的时间复杂度非常稳定，是(O(nlog n))，并且它还是原地排序算法。如此优秀，它是怎么做到的呢？

我们可以把堆排序的过程大致分解成两个大的步骤，建堆和排序。

1.建堆

我们首先将数组原地建成一个堆。所谓“原地”就是，不借助另一个数组，就在原数组上操作。建堆的过程，有两种思路。

第一种是借助我们前面讲的，在堆中插入一个元素的思路。尽管数组中包含(n)个数据，但是我们可以假设，起初堆中只包含一个数据，就是下标为(1)的数据。然后，我们调用前面讲的插入操作，将下标从(2)到(n)的数据依次插入到堆中。这样我们就将包含(n)个数据的数组，组织成了堆。

第二种实现思路，跟第一种截然相反，也是我这里要详细讲的。第一种建堆思路的处理过程是从前往后处理数组数据，并且每个数据插入堆中时，都是从下往上堆化。而第二种实现思路，是从后往前处理数组，并且每个数据都是从上往下堆化。

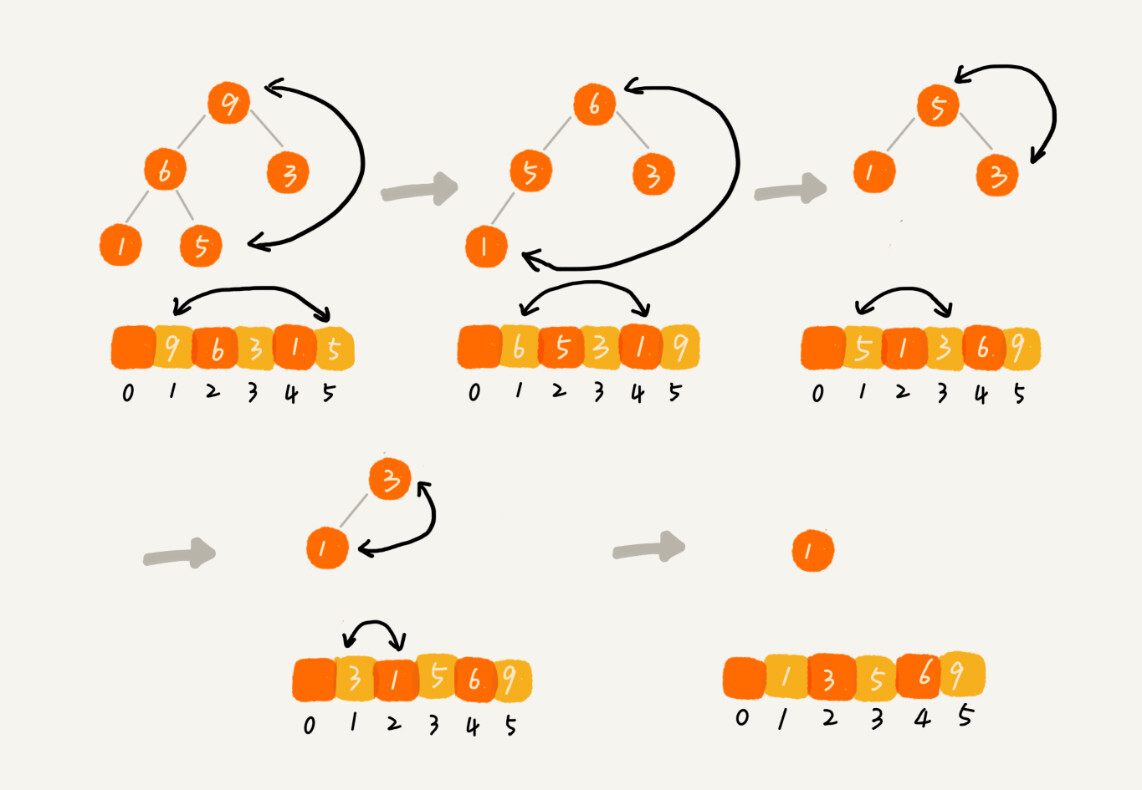
我举了一个例子，并且画了一个第二种实现思路的建堆分解步骤图，你可以看下。因为叶子节点往下堆化只能自己跟自己比较，所以我们直接从最后一个非叶子节点开始，依次堆化就行了。

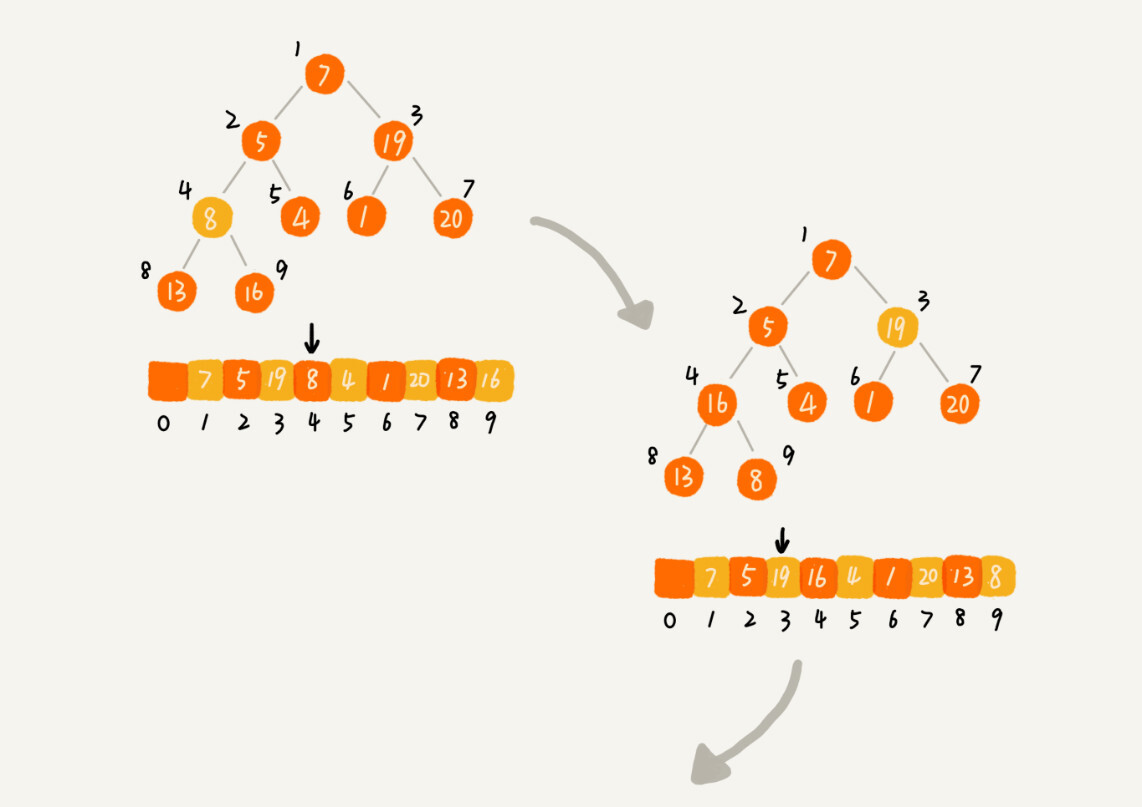
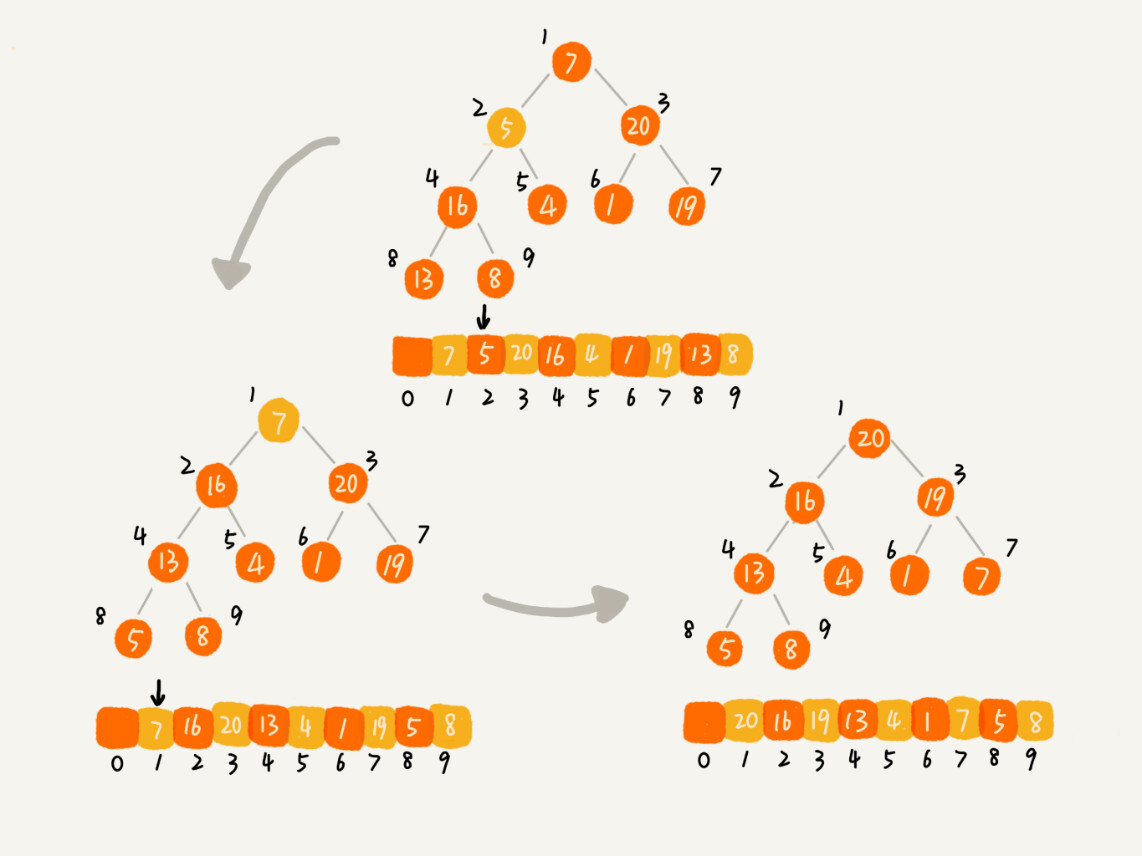
对于程序员来说，看代码可能更好理解一些，所以，我将第二种实现思路翻译成了代码，你可以看下。

private static void buildHeap(int[] a, int n) {

for (int i = n/2; i >= 1; --i) {

heapify(a, n, i);

}

}

private static void heapify(int[] a, int n, int i) {

while (true) {

int maxPos = i;

if (i2 <= n && a[i] < a[i2]) maxPos = i2;

if (i2+1 <= n && a[maxPos] < a[i2+1]) maxPos = i2+1;

if (maxPos == i) break;

swap(a, i, maxPos);

i = maxPos;

}

}

你可能已经发现了，在这段代码中，我们对下标从(frac{n}{2}) 开始到(1)的数据进行堆化，下标是(frac{n}{2}+1)到(n)的节点是叶子节点，我们不需要堆化。实际上，对于完全二叉树来说，下标从(frac{n}{2}+1)到(n)的节点都是叶子节点。

现在，我们来看，建堆操作的时间复杂度是多少呢？

每个节点堆化的时间复杂度是(O(log n))，那(frac{n}{2}+1)个节点堆化的总时间复杂度是不是就是(O(nlog n))呢？这个答案虽然也没错，但是这个值还是不够精确。实际上，堆排序的建堆过程的时间复杂度是(O(n))。我带你推导一下。

因为叶子节点不需要堆化，所以需要堆化的节点从倒数第二层开始。每个节点堆化的过程中，需要比较和交换的节点个数，跟这个节点的高度(k)成正比。

我把每一层的节点个数和对应的高度画了出来，你可以看看。我们只需要将每个节点的高度求和，得出的就是建堆的时间复杂度。

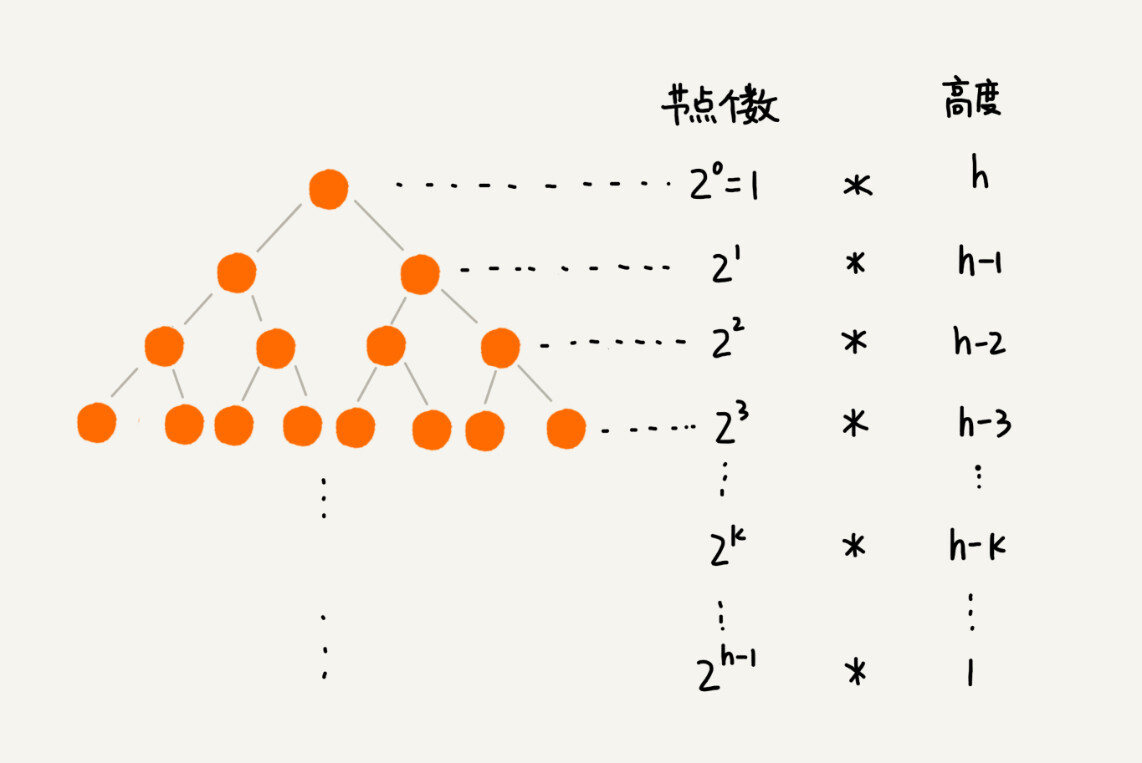
我们将每个非叶子节点的高度求和，就是下面这个公式：

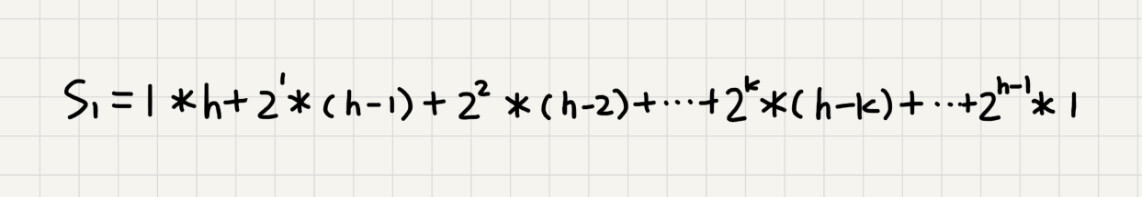
这个公式的求解稍微有点技巧，不过我们高中应该都学过：把公式左右都乘以(2)，就得到另一个公式(S2)。我们将(S2)错位对齐，并且用(S2)减去(S1)，可以得到(S)。

(S)的中间部分是一个等比数列，所以最后可以用等比数列的求和公式来计算，最终的结果就是下面图中画的这个样子。

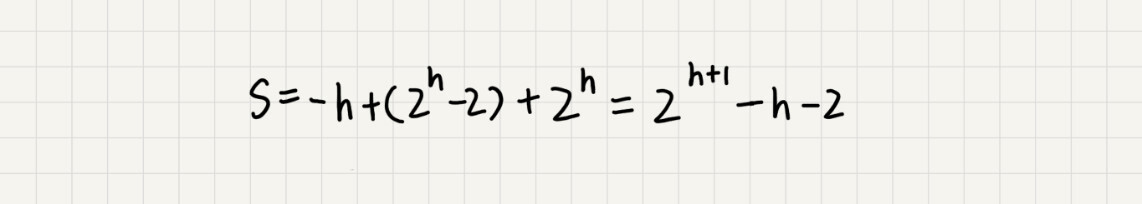
因为(h=log_{2}n)，代入公式(S)，就能得到(S=O(n))，所以，建堆的时间复杂度就是(O(n))。

2.排序

建堆结束之后，数组中的数据已经是按照大顶堆的特性来组织的。数组中的第一个元素就是堆顶，也就是最大的元素。我们把它跟最后一个元素交换，那最大元素就放到了下标为(n)的位置。

这个过程有点类似上面讲的“删除堆顶元素”的操作，当堆顶元素移除之后，我们把下标为(n)的元素放到堆顶，然后再通过堆化的方法，将剩下的(n-1)个元素重新构建成堆。堆化完成之后，我们再取堆顶的元素，放到下标是(n-1)的位置，一直重复这个过程，直到最后堆中只剩下标为(1)的一个元素，排序工作就完成了。

堆排序的过程，我也翻译成了代码。结合着代码看，你理解起来应该会更加容易。

// n表示数据的个数，数组a中的数据从下标1到n的位置。

public static void sort(int[] a, int n) {

buildHeap(a, n);

int k = n;

while (k > 1) {

swap(a, 1, k);

--k;

heapify(a, k, 1);

}

}

现在，我们再来分析一下堆排序的时间复杂度、空间复杂度以及稳定性。

整个堆排序的过程，都只需要极个别临时存储空间，所以堆排序是原地排序算法。堆排序包括建堆和排序两个操作，建堆过程的时间复杂度是(O(n))，排序过程的时间复杂度是(O(nlog n))，所以，堆排序整体的时间复杂度是(O(nlog n))。

堆排序不是稳定的排序算法，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作，所以就有可能改变值相同数据的原始相对顺序。

今天的内容到此就讲完了。我这里要稍微解释一下，在前面的讲解以及代码中，我都假设，堆中的数据是从数组下标为1的位置开始存储。那如果从(0)开始存储，实际上处理思路是没有任何变化的，唯一变化的，可能就是，代码实现的时候，计算子节点和父节点的下标的公式改变了。

如果节点的下标是(i)，那左子节点的下标就是(2*i+1)，右子节点的下标就是(2*i+2)，父节点的下标就是(frac{i-1}{2})。

解答开篇

现在我们来看开篇的问题，在实际开发中，为什么快速排序要比堆排序性能好？

我觉得主要有两方面的原因。

第一点，堆排序数据访问的方式没有快速排序友好。

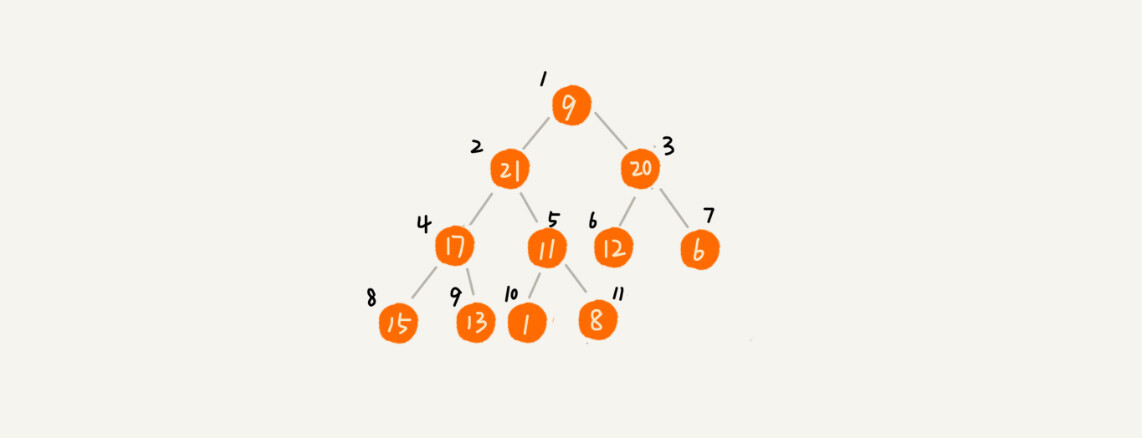
对于快速排序来说，数据是顺序访问的。而对于堆排序来说，数据是跳着访问的。 比如，堆排序中，最重要的一个操作就是数据的堆化。比如下面这个例子，对堆顶节点进行堆化，会依次访问数组下标是(1，2，4，8)的元素，而不是像快速排序那样，局部顺序访问，所以，这样对CPU缓存是不友好的。

第二点，对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序。

我们在讲排序的时候，提过两个概念，有序度和逆序度。对于基于比较的排序算法来说，整个排序过程就是由两个基本的操作组成的，比较和交换（或移动）。快速排序数据交换的次数不会比逆序度多。

但是堆排序的第一步是建堆，建堆的过程会打乱数据原有的相对先后顺序，导致原数据的有序度降低。比如，对于一组已经有序的数据来说，经过建堆之后，数据反而变得更无序了。

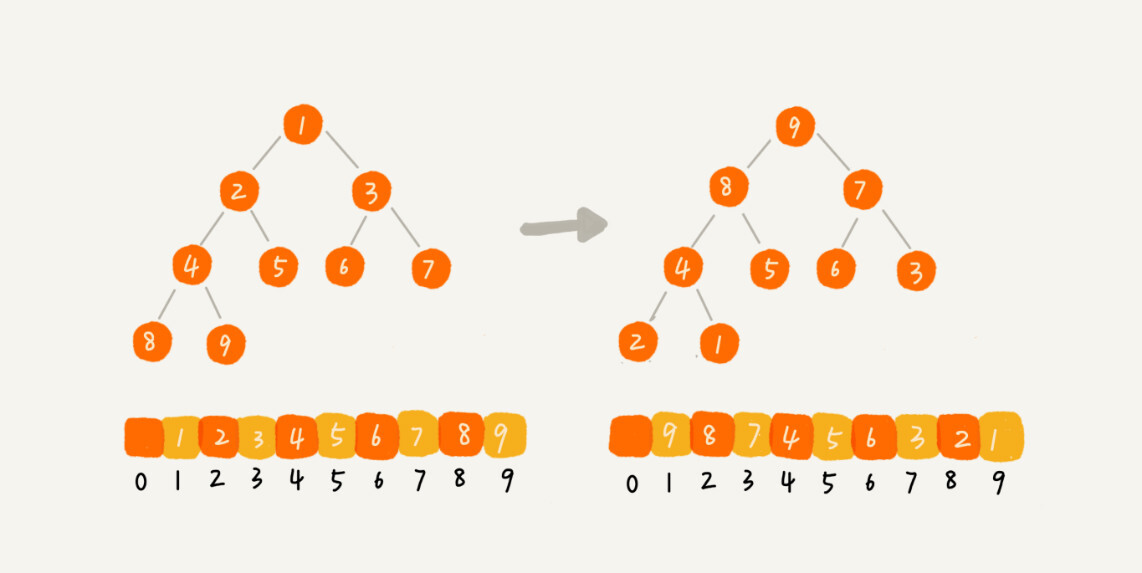
对于第二点，你可以自己做个试验看下。我们用一个记录交换次数的变量，在代码中，每次交换的时候，我们就对这个变量加一，排序完成之后，这个变量的值就是总的数据交换次数。这样你就能很直观地理解我刚刚说的，堆排序比快速排序交换次数多。

内容小结

今天我们讲了堆这种数据结构。堆是一种完全二叉树。它最大的特性是：每个节点的值都大于等于（或小于等于）其子树节点的值。因此，堆被分成了两类，大顶堆和小顶堆。

堆中比较重要的两个操作是插入一个数据和删除堆顶元素。这两个操作都要用到堆化。插入一个数据的时候，我们把新插入的数据放到数组的最后，然后从下往上堆化；删除堆顶数据的时候，我们把数组中的最后一个元素放到堆顶，然后从上往下堆化。这两个操作时间复杂度都是(O(log n))。

除此之外，我们还讲了堆的一个经典应用，堆排序。堆排序包含两个过程，建堆和排序。我们将下标从(frac{n}{2})到(1)的节点，依次进行从上到下的堆化操作，然后就可以将数组中的数据组织成堆这种数据结构。接下来，我们迭代地将堆顶的元素放到堆的末尾，并将堆的大小减一，然后再堆化，重复这个过程，直到堆中只剩下一个元素，整个数组中的数据就都有序排列了。

课后思考

1. 在讲堆排序建堆的时候，我说到，对于完全二叉树来说，下标从$frac{n}{2}+1$到$n$的都是叶子节点，这个结论是怎么推导出来的呢？

2. 我们今天讲了堆的一种经典应用，堆排序。关于堆，你还能想到它的其他应用吗？

欢迎留言和我分享，我会第一时间给你反馈。