HDU1010 Tempter of the Bone

1. 题面
        
2. 题目大意
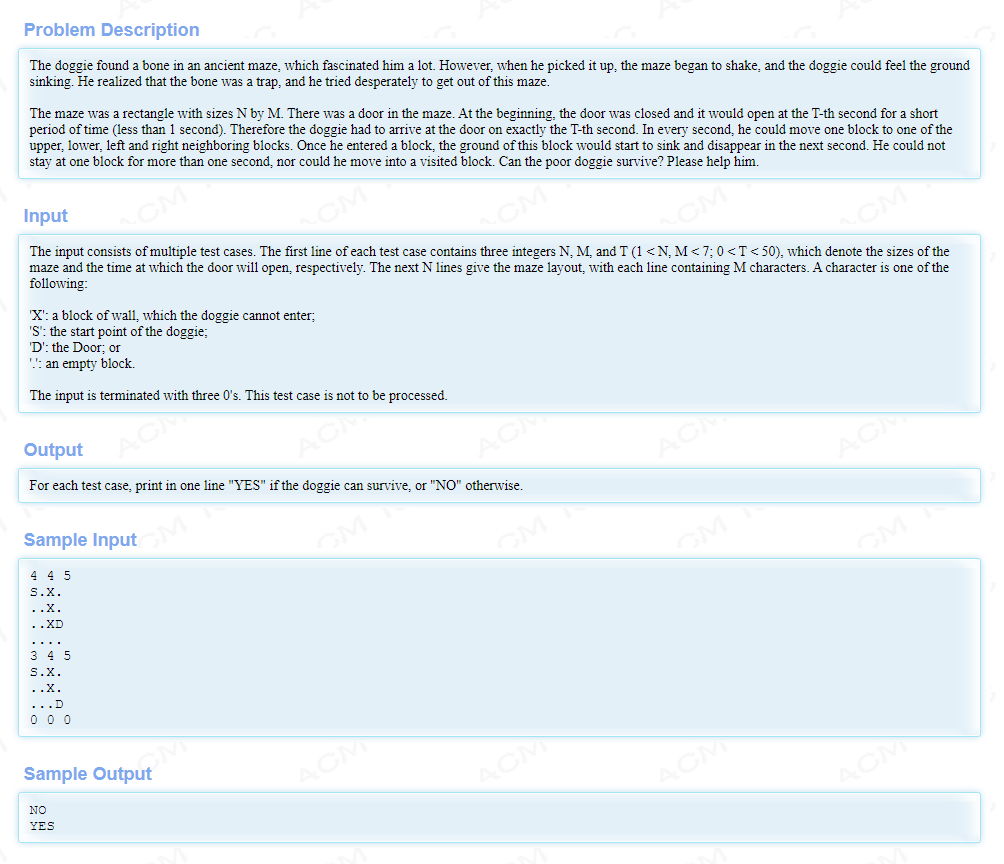
   给定一个(n*m)的迷宫，里面有一扇门(终点)，会在第(T)秒打开；走过的路不能再走；
3. 算法
          本题DFS+两种剪枝
   不过在说正解之前，我们先来讨论一下为什么不能用BFS
   本题提到了两点，一是走过的路只能待一秒，二是门只会打开不到一秒。这两点说明我们只能在(T)秒时到达门，而迷宫中有时会存在一条路径用时比(T)秒更短，我们就需要绕路。BFS一般用来求最短路径，不能满足绕路的需求，所以不行
4. 正解
   此题十分简单，(90)分困难。原因在于有一个特别的剪枝——奇偶剪枝
   现在将地图抽象为一个(01)矩阵

[egin{bmatrix} 0 & 1 & 0 & 1 & 0 & 1 \ 1 & 0 & 1 & 0 & 1 & 0 \ 0 & 1 & 0 & 1 & 0 & 1 \ 1 & 0 & 1 & 0 & 1 & 0 \ 0 & 1 & 0 & 1 & 0 & 1 \ end{bmatrix} ]

其中从(0)到达(1)需要1步，从一个(1)到达另外(1)需要2步。更一般的，从任意一个(0)到达任意一个(1)需要奇数步，从任意一个(1)到达另外任意一个(1)需要偶数步。
如果起点和终点的奇偶性相同，则(T)必须为偶数，因为只有偶数步才能到达，我们可以利用这个性质在输入时判断是否可以到达终点。这种剪枝属于可行性剪枝
还有，在搜索步数已经超过T时，直接返回(0)即可，因为小狗已经出不去了。这种剪枝被称为最优性剪枝。
5. 代码

#include<bits/stdc++.h>
using namespace std;

const int N = 10;
const int dir_x[7] = {0,0,1,0,-1};
const int dir_y[7] = {0,1,0,-1,0};

bool flag = 0;
int n,m,T;
int sx,sy,dx,dy;
char a[N][N];
bool v[N][N];

void dfs(int x,int y,int t)
{
	v[x][y] = 1;
	if(a[x][y] == 'D')
	{
		if(t == T) flag = 1;
		return; 
	}
	
	int tmp = T - t - abs(dx-x) - abs(dy-y);//检查当前点是否能到达 
    if(tmp < 0 || tmp&1) return;//不行返回 
	
	if(t > T) return;//超时了也返回 
	
	for(int i = 1;i <= 4;i ++ )
	{
		int xx = x + dir_x[i];
		int yy = y + dir_y[i];
		if(xx >= 1 && xx <= n && yy >= 1 && yy <= m && a[xx][yy] != 'X' && !v[xx][yy])
		{
			dfs(xx,yy,t + 1);
			if(flag) return;
			v[xx][yy] = 0;
		}
	}
}

int main()
{
	cin >> n >> m >> T;
	while(n != 0 || m != 0 || T != 0)
	{
		for(int i = 1;i <= n;i ++ )
		{
			for(int j = 1;j <= m;j ++ )
			{
				cin >> a[i][j];
				if(a[i][j] == 'S')
				{
					sx = i;
					sy = j;
				}
				if(a[i][j] == 'D')
				{
					dx = i;
					dy = j;
				}
			}
		}
		
		memset(v,0,sizeof v);
		flag = 0;
		dfs(sx,sy,0);
		
		if(flag) cout << "YES" << endl;
		else cout << "NO" << endl;
		cin >> n >> m >> T;
	}
	return 0;
}

6. 剪枝方法（以下内容摘自李煜东《算法竞赛进阶指南》ISBN 978-7-83009-313-6）
   剪枝，就是减小搜索树规模、尽早排除搜索树中不必要的分支的一种手段。形象地看，就好像剪掉了搜索树的枝条，故被称为“剪枝”。在深度优先搜索中，有以下几类常见的剪枝方法：

• 优化搜索顺序
  在一些问题中，搜索树的各个层次、各个分支之间的顺序不是固定的。不同的搜索顺序会产生不同的搜索树形态，其规模大小也相差甚远。
• 排除等效冗余
  在搜索过程中，如果我们能够判定从搜索树的当前节点上沿着某几条不同分支到达的子树是等效的，那么只需要对其中的一条分支执行搜索。初学者一定要避免重叠、混淆“层次”与“分支”，避免遍历若干棵覆盖同一状态空间的等效搜索树。
• 可行性剪枝
  在搜索过程中，及时对当前状态进行检查,如果发现分支已经无法到达递归边界，就执行回溯。这就好比我们在道路上行走时，远远看到前方是一个死胡同，就应该立即折返绕路，而不是走到路的尽头再返回。
  某些题目条件的范围限制是一个区间，此时可行性剪枝也被称为“上下界剪枝”。
• 最优性剪枝
  在最优化问题的搜索过程中，如果当前花费的代价已经超过了当前搜到的最优解，那么无论采取多么优秀的策略到达递归边界，都不可能更新答案。此时可以停止对当前分支的搜索，执行回溯。
• 记忆化
  可以记录每个状态的搜索结果，在重复遍历一个状态时直接检索并返回。这就好比我们对图进行深度优先遍历时，标记一个节点是否己经被访问过。