dfs序+线段树,啥?如果在一棵树上,需要你修改一些节点和查询一些节点,如果直接dfs搜的话肯定超时,那用线段树?树结构不是区间啊,怎么用?用dfs序将树结构转化为一个区间,就能用线段树进行维护了。
dfs序是指:每个节点在dfs深度优先遍历中的进出栈的时间序列,记录每个点进栈和出栈的时间点,会发现每个点在栈中出现两次
比如下面这个图的dfs序:
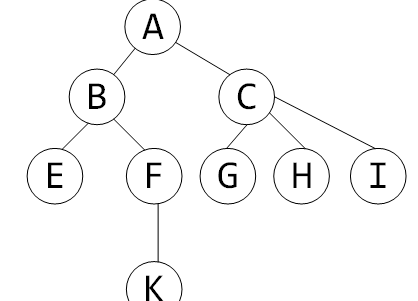 (转载来的图片,太懒不想画)
(转载来的图片,太懒不想画)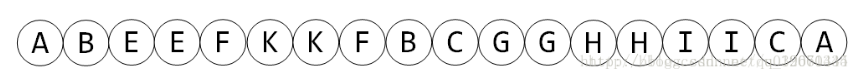
那么这样转化后我们就可以在上面进行线段树了。对于进栈时间点,我们记录为left[ u ],出栈时间点为right[ u ] 。对于这个区间,我们将每个节点标记为 1~len(dfs序长度)
以这个为区间1~len建线段树,然后那棵树就没用了!,没用了!对于修改一个节点x,就是修改left[x](但你的len是等于n的,或者你如果建的是两个节点都算的,你需要update左右编号),对于查询一个区间,就是查询left[x]~right[x],实际上就是线段树。
但是我在刚理解时候总会受原来那颗树的影响,实际上,可以这样理解,比如在这个dfs序中你要修改树节点1(原本的值都是1)
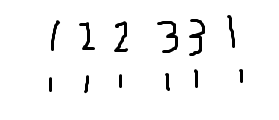 ------------------------------>
------------------------------>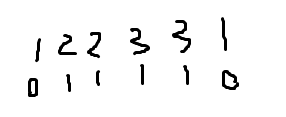
附上一个例题
There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.
The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?
Input
The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning
Output
Sample Input
3 1 2 1 3 3 Q 1 C 2 Q 1
Sample Output
3 2
1 var 2 left,right,next,head,a,value:array[0..800005]of longint; 3 n,m,k,x,y,e,tot,s:longint; 4 i:longint; 5 ch:char; 6 procedure add(x,y:int64); 7 begin 8 inc(e);a[e]:=y;next[e]:=head[x];head[x]:=e; 9 end; 10 procedure dfs(u,m:longint); 11 var i,v:longint; 12 begin 13 inc(tot); 14 left[u]:=tot; 15 i:=head[u]; 16 while i>0 do 17 begin 18 v:=a[i]; 19 if v<>m then begin dfs(v,u); end; 20 i:=next[i]; 21 end; 22 // inc(tot); 23 right[u]:=tot; 24 25 end; 26 procedure build(u,l,r:longint); 27 var mid:longint; 28 begin 29 if l=r then 30 begin 31 value[u]:=1; 32 exit; 33 end; 34 mid:=(l+r)>>1; 35 build(u*2,l,mid); 36 build(u*2+1,mid+1,r); 37 value[u]:=value[u*2]+value[u*2+1]; 38 end; 39 procedure upate(u,id,l,r:longint);//id 为修改点位置 40 var mid:longint; 41 begin 42 if (l>id)or(r<id) then exit; 43 if (l=id)and(r=id) then 44 begin 45 if value[u]=1 then value[u]:=0 else value[u]:=1; 46 exit; 47 end; 48 mid:=(l+r)>>1; 49 upate(u*2,id,l,mid); 50 upate(u*2+1,id,mid+1,r); 51 value[u]:=value[u*2]+value[u*2+1]; 52 end; 53 function que(u,l,r,ql,qr:int64):int64; 54 var mid:longint; 55 begin 56 if (ql>r)or(qr<l) then exit(0); 57 if (ql<=l)and(r<=qr) then exit(value[u]); 58 mid:=(l+r)>>1; 59 exit(que(u*2,l,mid,ql,qr)+que(u*2+1,mid+1,r,ql,qr)); 60 end; 61 begin 62 readln(n); 63 for i:=1 to n-1 do 64 begin 65 readln(x,y); 66 add(x,y); 67 add(y,x); 68 end; 69 dfs(1,1); 70 build(1,1,tot); 71 readln(k); 72 for i:=1 to k do 73 begin 74 readln(ch,s); 75 if ch='Q' then writeln(que(1,1,tot,left[s],right[s]))else 76 begin 77 upate(1,left[s],1,tot); 78 // upate(1,right[s],1,tot); 79 end; 80 end; 81 end.