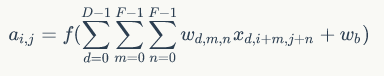1. 卷积运算
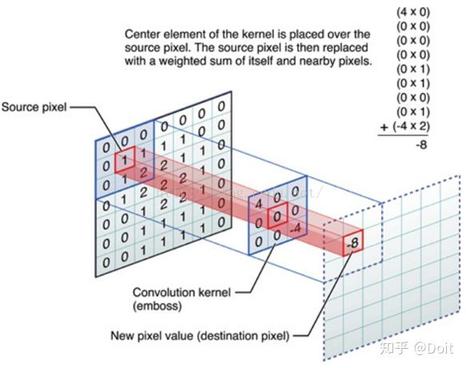
卷积运算不再是识别一个个的像素点,而是用卷积核识别一个一个的像素区域。
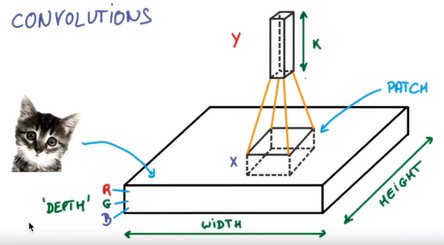
卷积一次之后,图像的长宽更小,但高度更高(除了原本的RGB,又增加了一些边缘信息)。
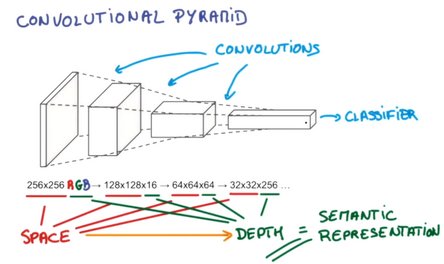
-
stride: 卷积核每次移动的跨度
-
padding: 边缘填充
一般来说,filter的边长大于stride,会造成每次移动滑窗后有交集部分,交集部分意味着多次提取特征,尤其表现在图像的中间区域提取次数较多,边缘部分提取次数较少,怎么办?
方法是在图像外围加一圈'0'作为填充。

每次卷积时,会无意的丢失一些信息,故而使用池化——卷积时不压缩长宽,而通过池化进行。
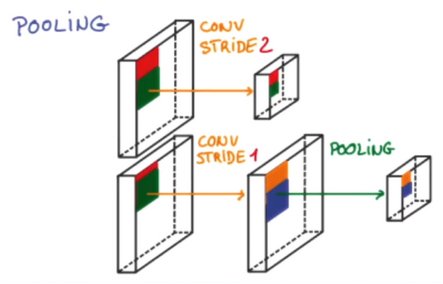
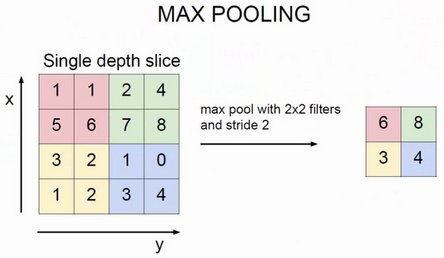
池化(Pooling)是卷积神经网络中的一个重要的概念,它实际上是一种形式的降采样。有多种不同形式的非线性池化函数,而其中“最大池化(Max pooling)”是最为常见的。它是将输入的图像划分为若干个矩形区域,对每个子区域输出最大值。
直觉上,这种机制能够有效的原因在于,在发现一个特征之后,它的精确位置远不及它和其他特征的相对位置的关系重要。池化层会不断地减小数据的空间大小,因此参数的数量和计算量也会下降,这在一定程度上也控制了过拟合。
通常来说,CNN的卷积层之间都会周期性地插入池化层。
由于池化层过快地减少了数据的大小,目前文献中的趋势是使用较小的池化滤镜,甚至不再使用池化层。
2. 卷积核(kernel, or filter)
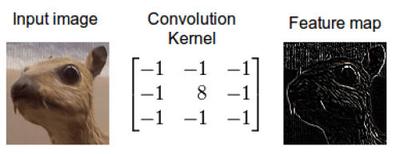
卷积核的输出是一幅修改后的图像,在深度学习中经常被称作feature map。
注意:通过单个卷积核运算后,得到的是一个二维(深度为1)的Featrue-map。

我的同事Jannek Thomas通过索贝尔边缘检测滤波器(与上上一幅图类似)去掉了图像中除了边缘之外的所有信息——这也是为什么卷积应用经常被称作滤波而卷积核经常被称作滤波器(更准确的定义在下面)的原因。由边缘检测滤波器生成的feature map对区分衣服类型非常有用,因为只有外形信息被保留下来。
每个卷积核具有长、宽、深三个维度。在CNN的一个卷积层中:
-
卷积核的长、宽都是人为指定的,长X宽也被称为卷积核的尺寸,常用的尺寸为3x3,5x5等;
-
卷积核的深度与当前图像的深度(feather map的张数)相同,所以指定卷积核时,只需指定其长和宽两个参数。
- 假设inpute的四个维度是 [batch, in_height, in_width, in_channels]
- 那么filter的四个维度是 [filter_height, filter_width, in_channels, out_channels]
一般使用多个filter分别进行卷积,最终得到多个特征图。
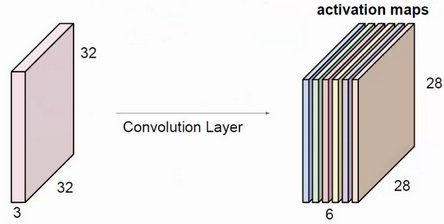
上图使用了6个filter分别卷积进行特征提取,最终得到6个特征图。将这6层叠在一起就得到了卷积层输出的结果。
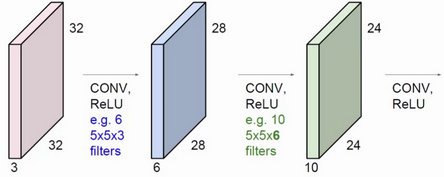
卷积不仅限于对原始输入的卷积。蓝色方块是在原始输入上进行卷积操作,使用了6个filter得到了6个提取特征图。绿色方块还能对蓝色方块进行卷积操作,使用了10个filter得到了10个特征图。每一个filter的深度必须与上一层输入的深度相等。
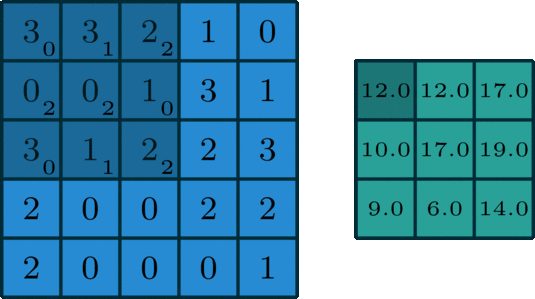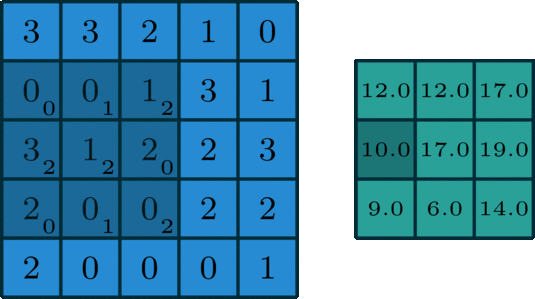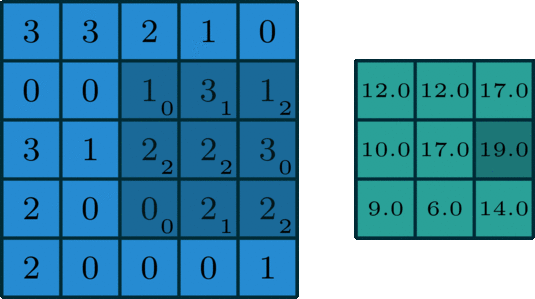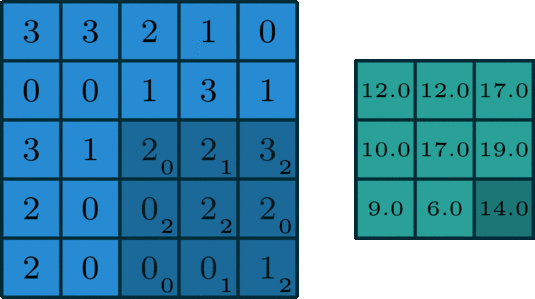
例如:
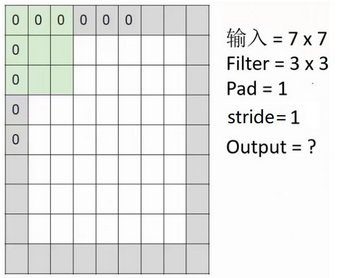
请计算上图中Output=?
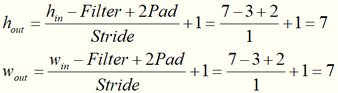
2.1. 自定义卷积核
除非指定了卷积核(例如OpenCV中使用特定的卷积核提取轮廓信息或去除噪音),否则kernel不是一个定值。在深度学习中,kernel是需要随着训练和反馈,不断更新的——权重信息将记录在kernel中。
对于Conv2D(),它随机初始化了filters个卷积核,并且每个卷积核都在每次的训练中更新权值。
需要自己定义卷积核的目的:目前是需要通过一个VGG网络提取特征特后需要对其进行高斯卷积,卷积后再继续输入到网络中训练。
2.2. 多层卷积

以上图为例:
- 第一次卷积可以提取出低层次的特征。
- 第二次卷积可以提取出中层次的特征。
- 第三次卷积可以提取出高层次的特征。
特征是不断进行提取和压缩的,最终能得到比较高层次特征,简言之就是对原式特征一步又一步的浓缩,最终得到的特征更可靠。利用最后一层特征可以做各种任务:比如分类、回归等。
2.3. 权值共享
在卷积神经网络中,有一个非常重要的特性:权值共享。
所谓的权值共享就是说,给一张输入图片,用一个filter去扫这张图,filter里面的数就叫权重,这张图每个位置是被同样的filter扫的,所以权重是一样的,也就是共享。
3. 卷积计算
例如输入224x224x3(rgb三通道),输出是32位深度,卷积核尺寸为5x5。
那么我们需要32个卷积核,每一个的尺寸为5x5x3(最后的3就是原图的rgb位深3),每一个卷积核的每一层是5x5(共3层)分别与原图的每层224x224卷积,然后将得到的三张新图叠加(算术求和),变成一张新的feature map。 每一个卷积核都这样操作,就可以得到32张新的feature map了。
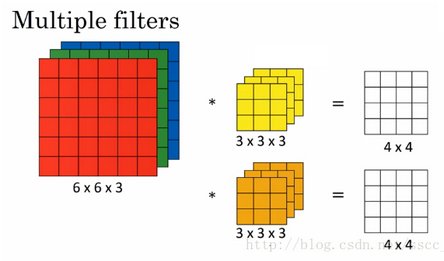
也就是说,不管输入图像的深度为多少,经过一个卷积核(filter),最后都通过下面的公式变成一个深度为1的特征图。