机器学习
特征工程
特征抽取
字典特征抽取
sklearn.feature_extraction.DictVectorizer
类DictVectorizer(sparse=True) 如果sparse=False 则返回列表
.fit_transform(X) X是字典或者包含字典的迭代器 返回sparse矩阵
.inverse_transform(X) X 数组 或者sparse矩阵 返回之前的数据格式
.get_feature_names() 返回类别名称
.transform(X) 按照原先的标准转换
sparse矩阵 节约内存 方便读取处理
vector = DictVectorizer() # 对字典进行特征值化 data = [ {'city':'北京', 'name':123}, {'city':'上海', 'name':1235}, {'city':'广州', 'name':1255}, {'city':'扬州', 'name':15}, ] res = vector.fit_transform(data) print(vector.get_feature_names()) print(res) print(res.toarray())
文本特征抽取
sklearn.feature_extraction.text.CountVectorizer
类DictVectorizer()
.fit_transform(X) X是字符串或者包含字符串的迭代器 返回sparse矩阵
.inverse_transform(X) X 数组 或者sparse矩阵 返回之前的数据格式
.get_feature_names() 返回类别名称
.transform(X) 按照原先的标准转换
cut_word采用了jieba库
def cut_word(string): import jieba c = jieba.cut(string) c_list = list(c) return ' '.join(c_list) def text_vector(): from sklearn.feature_extraction import text vector = text.CountVectorizer() # 对文本进行特征值化 data = '中文特征值,中文真好用,特征值真好用' s = cut_word(data) res = vector.fit_transform([s]) print(vector.get_feature_names()) print(res) print(res.toarray())
tf-idf特征抽取
朴素贝叶斯算法 需要用到
term frequency 词频
inverse document frequency
log(总文档数量/该词出现的文档数量)
tf * idf 重要性
sklearn.feature_extraction.text.TfidfVectorizer
返回重要性矩阵
方法和之前的类似.
类TfidfVectorizer(stop_words=None) stop_words为屏蔽的词语列表.
.fit_transform(X) X是字符串或者包含字符串的迭代器 返回sparse矩阵
.inverse_transform(X) X 数组 或者sparse矩阵 返回之前的数据格式
.get_feature_names() 返回类别名称
特征预处理
通过特定的统计方法(数学方法), 将数据转化为算法要求的数据
数值型数据 标准缩放
归一化
标准化
缺失值
sklearn.preprocessing
__all__ = [
'Binarizer',
'FunctionTransformer',
'Imputer',
'KBinsDiscretizer',
'KernelCenterer',
'LabelBinarizer',
'LabelEncoder',
'MultiLabelBinarizer',
'MinMaxScaler',
'MaxAbsScaler',
'QuantileTransformer',
'Normalizer',
'OneHotEncoder',
'OrdinalEncoder',
'PowerTransformer',
'RobustScaler',
'StandardScaler',
'add_dummy_feature',
'PolynomialFeatures',
'binarize',
'normalize',
'scale',
'robust_scale',
'maxabs_scale',
'minmax_scale',
'label_binarize',
'quantile_transform',
'power_transform',
]
归一化:
映射到默认[0,1] 或者通过feature_range设置
mm = MinMaxScaler(feature_range=(3, 5)) #实例化 data = mm.fit_transform([[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]) print(data)
[[5. 3. 3. 3. ]
[3. 5. 5. 4.66666667]
[4. 4. 4.2 5. ]]
缺点:容易受异常点影响 鲁棒性较差. 传统精确小数据场景
标准化:
均值为0, 方差为1的标准内
std = StandardScaler() data = std.fit_transform([[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]) print(data) print(std.mean_)
适合大数据场景, 异常点影响不大
缺失值:
删除或者插补
.Imputer(missing_value='NaN', strategy='mean', axis=0) 策略是用mean(平均数) 来填补NaN axis=0时按列填补(特征)
Imputer.fit_transform(X) X 是narray的格式 返回同等规模的
缺失值必须是np.nan 不能是其他字符
数据降维
维度: 特征的数量
1.特征选择
.feature_selection
原因:
1.冗余 相关度高 增加了计算负荷
2.噪声 部分特征对预测结果有影响
主要方法:
Filter 过滤式 VarianceThreshold
.VarianceThreshold(threshold=0.0)
删除方差低于0.0的特征 默认为0
Embedded嵌入式 正则化 决策树
Wrapper 包裹式
神经网络
2.主成分分析
.decomposition
PCA principle Component Analysis
目的:使数据压缩,尽可能降低数据维度,损失少量信息
特征数量达到上百的时候 考虑数据简化问题
数据会改变 特征数量减少

PCA(n_components=None)
0.9-0.95 表示保留90%-95%的信息 是可以不断调的
如果是整数 表示减少到的特征数量 一般不使用
数据
建议
训练集 约75%
测试集 约25%
用训练集来建立模型, 用测试集来评估模型
数据集划分的API:
.model_selection.train_test_split(*arrays. **options)
特征值
目标值
test_size 测试集的大小 25%
random_state 随机数种子
数据集的API :
.datasets
datasets.load_*() 小规模数据集
datasets.fetch_*(data_home=None) 从网上下载的大规模数据
返回的数据是字典类型
data: 特征数据数组 ndarray
target 标签数组
DESCR 数据描述
feature_names 特征名 新闻数据 手写数字 回归数据没有
target_names 标签名
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split li = load_iris() # print(li.data) # print(li.target) # print(li.DESCR) # 顺序固定 x_train, x_test, y_train, y_test = train_test_split(li.data, li.target, test_size=0.25) print(x_train, y_train) # 训练集的特征数据和目标值 print(x_test, y_test) # 测试集的特征数据和目标值
转换器与预估器
之前的处理就是转换器 是实现特征工程的API
fit_transform方法, 先fit() 把数据复制进去 算出平均值标准差等 再transform() 对数据进行转换
预估器 estimator 是实现算法的API
用于分类的预估器
sklearn.neighbor K邻近算法
sklearn.naive_bayes 贝叶斯
sklearn.linear_model.LogisticRegression 逻辑回归
sklearn.tree 决策树与随机森林
用于回归的预估器
sklearn.linear_model.LinearRegression 线性回归
sklearn.linear_model.Ridge 岭回归
用于聚类的预估器....
1.调用fit(x_train,y_train)
2.
predict(x_test)
score(x_test,y_test)
分类算法
K近邻算法
计算距离 找到最近的K个点 大部分是属于哪一类就是哪一类
from sklearn.neighbors import KNeighborsClassifier knn = KNeighborsClassifier(n_neighbors=5) knn.fit(data) predict_ = knn.predict(x_test)
朴素贝叶斯
求出属于每个类别的概率 找出概率最大者
必须 特征独立 ----朴素

C 某一类别
W 特征集
有一定可能最后结果是0, 因为这个词在训练的样本中从未出现过

m为特征值的个数, 即W集的个数
.naive_bayes.MultinomialNB(alpha=1.0)
alpha即为拉普拉斯平滑系数
特点:
分类效率稳定
对缺失数据不太敏感, 算法简单 不需要调参 常用于文本分类
准确率高, 速度快
缺点:
受训练数据影响特别大
特征必须独立存在(朴素)
文本分类而言, 神经网络效果比朴素贝叶斯更好
分类模型的评估
准确率
预测对的占总数据的百分比
召回率
预测正确的占所有正确的数据的百分比

精确率
预测正确的占预测为正确值的百分比

F1-score
分类评估的API
.metrics.classfication_report(y_true, y_predict, target_names=None)
模型选择与调优
交叉验证 不包括测试集 cross validation

求平均值
网格搜索 调参数
每组超参数用交叉验证来评估
API
.model_selection.GridSearchCV(estimator, param_grid=None, cv=None)
estimator 估计其对象
param_grid 给一些值,存放在字典中
cv 用几折交叉验证
然后用fit()输入数据
best_score_:
best_estimator_:
cv_results:
from sklearn.neighbors import KNeighborsClassifier from sklearn.model_selection import train_test_split from sklearn.datasets import load_iris from sklearn.model_selection import GridSearchCV knn = KNeighborsClassifier() li = load_iris() x_train, x_test, y_train, y_test = train_test_split(li.data, li.target, test_size=0.25) param = {"n_neighbors": [2, 3, 4, 5, 6, 7, 8, 9, 10]} gc = GridSearchCV(knn, param_grid=param, cv=10) gc.fit(x_train, y_train) print("测试集上的准确率", gc.score(x_test, y_test)) print("交叉验证中最好的结果", gc.best_score_) print("最好的模型", gc.best_estimator_) print("每次交叉验证的结果", gc.cv_results_)
决策树与随机森林
信息熵
信息增益:一个特征条件之后,减少的信息熵的大小

决策树的分类依据:信息增益
基尼系数 划分更加仔细
API:
.tree.DecisionTreeClassfier(criterion='gini', max_depth=None)
默认基尼系数 也可以改为 entropy 信息增益
优点:
简单的理解 树木可视化
需要很少的数据准备, 其他技术通常需要数据归一化
缺点
不能很好地推广数据过于复杂的树
过拟合
改进
剪枝
随机森林
随机森林API
.ensemble.RandomForestClassifier(n_estimator=10, criterion='gini', max_depth=None, bootstrap=True, random_state=None, max_feature = 'auto')
优点:
极好的准确率
有效的运行在大数据上
处理具有高维特征的输入样本 不需要降维
评估各个特征在分类问题上的重要性

逻辑回归
回归算法
线性回归
聚类算法
K-means算法
K,即簇的个数 分为几类
质心: 均值 向量各维取平均
距离的度量: 欧氏距离 余弦相似度
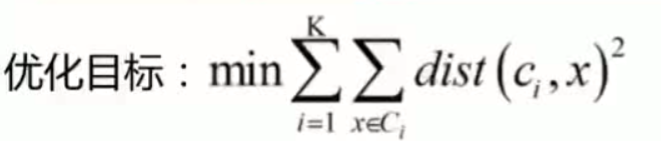
劣势
1.初值对结果影响特别大
2.如下图
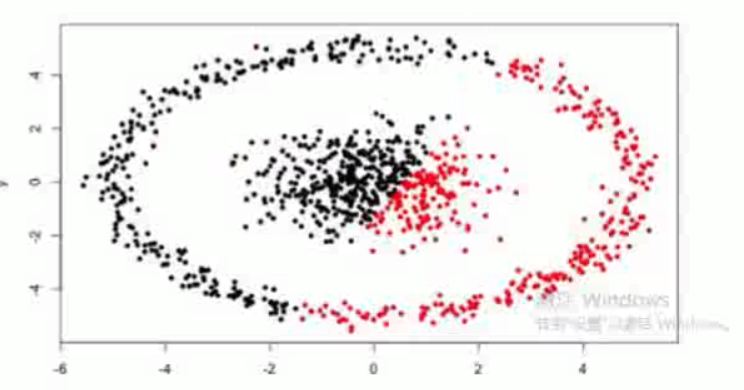
DBSCAN算法 Density-Based Spatial Clustering of Applications with Noise
核心对象: 若某个点的密度达到算法设定的阈值则称其为核心点(即r邻域内点的数量不小于minPts)
∈-邻域的距离阈值: 设定的半径r
直接密度可达: 若某点p在点q的r邻域内 且q是核心点 则p-q直接密度可达
密度可达: 若有一个点的序列 q0, q1, ...,qk 对任意qi和qi-1是直接密度可达的, 则称 从q0 到 qk 密度可达 实际上是直接密度可达的传播
密度相连: 若从某核心点p出发, 点q和点k都是密度可达的, 则称点q和点k是密度相连的
边界点: 属于某一个类的非核心点, 不能发展下线了
噪声点: 不属于任何一个类簇的点, 从任何一个核心出发都是密度不可达的
参数的选择:
半径的选择: 根据K距离设定 找突变点
K距离: 给定数据集 计算所有每两点之间的距离 从小到大排列 第k个就称为K距离
优势:
不需要指定簇的个数
可以发现任意形状的簇
擅长找离群点
两个参数
劣势:
高位数据处理困难(需降维)
参数难以选择(参数对结果影响特别大)
Sklearn中效率很慢(数据削减策略)
EM算法(Expectation-maximization):
期望最大算法是一种从不完全数据或有数据丢失的数据集(存在隐含变量)中求解概率模型参数的最大似然估计方法。 聚类算法
https://blog.csdn.net/zouxy09/article/details/8537620
EM算法流程
1.初始化分布参数θ
2.E-step 根据参数θ计算每个样本属于zi的概率( 也就是Q)
3.M-step 根据 Q, 求出含有θ的似然函数的下界并最大化 得到新的θ
4.不断迭代下去
GMM(高斯混合模型)
数据可以看成是从数个高斯分布中生成的
每个高斯分布称为一个component
类似K-means算法, 求解方式EM 不断的更新迭代