我本着公平公开公正的态度作出以下评价:
1、面向对象真的很修身养性
2、有一个好的身体非常重要
3、互相hack可以暴露人的阴暗面
好了,步入正题。
一、作业分析
1、第一次作业分析
1.1类图
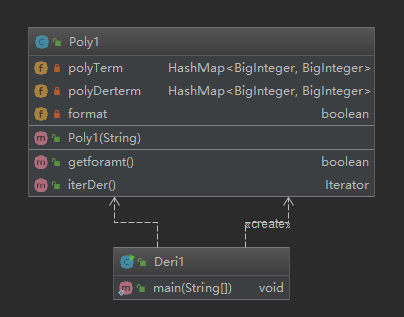
1.1.2基于度量的分析
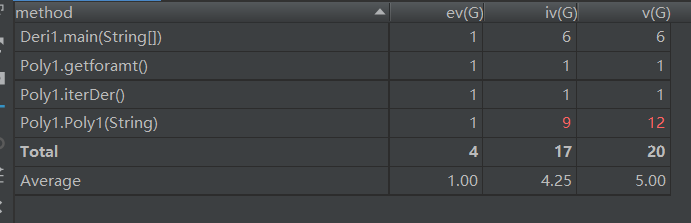
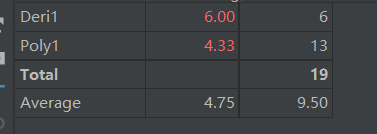
由于只有两个类,而Deri()类几乎什么都没做的,导致Poly类的复杂度较高。一开始写OO当成面向过程来写,结果把大部分功能都放在构造函数里面一起实现了。
1.2心路历程思考过程
当时对于面向对象没什么概念,照着面向过程就去写代码了。第一次作业是简单的多项式,两个类解决问题,一个用来存储,一个用来求导。(事实上,在写代码的时候,求导过程和存储放在了一起,而Derivation类形同虚设,只是一个main()函数)。由于第一次的输入比较简单,和大部分人一样,我选择了大正则匹配,将匹配到的单项式存入Polynomial,并完成求导,再将求导结果返回给Derivativation。而格式判断的工作则是在正则匹配时不停地删去已匹配的项,若字符串最后为空,即格式正确。
1.3制造bug的原因
一个主要bug是空白符的问题,指导书中只要求space和 ,而我用s实现的空格匹配。
2、第二次作业分析
2.1类图

2.1.2基于度量的分析
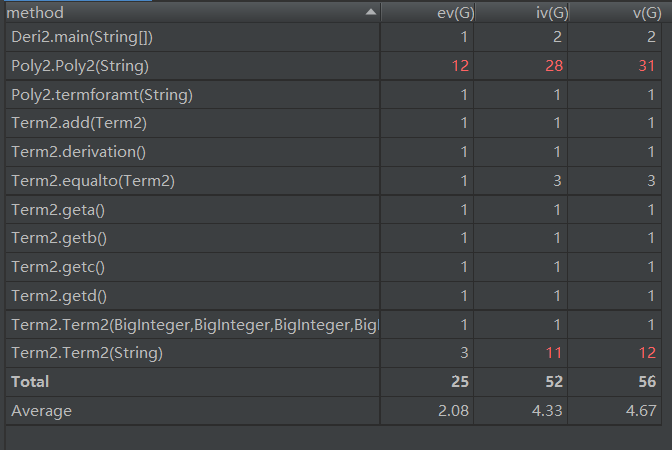
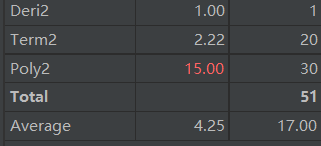
可以看出,实例化一个对象的复杂度较高,尤其是Poly类。这次作业和第一次作业一样,把大部分功能都放在了构造函数当中。
2.2思考过程
第二次作业引入了三角函数sin(x)和cos(x),相较于第一次的正则,这一次更加复杂,但是我们依然可以选择头铁的用大正则解决(会面临爆栈问题),这样就连格式判断的问题也一并解决了。在匹配到单项式之后,先进行通过replace操作将所有单项式符号归一化以方便后续处理(例如:删空格,删加号,减号合并),再对单项式进行逐个读入,存储系数和三个指数。并且增加了equal()方法和add()方法用来合并同类项。求导操作也是在Term类里完成的。最后的简化输出则由Poly类实现,但是在实现过程要不断向Term索要指数,系数,不得不增加geta(),getb(),getc(),getd()四个方法,这属于设计上的纰漏。
2.3制造bug的原因
在Term初步归一化时,前置负号没有处理(其实处理了,半夜误删了那一段代码)。
没有仔细看指导书,在Poly类里少了两种空格插入的情况。
3、第三次作业分析
3.1类图
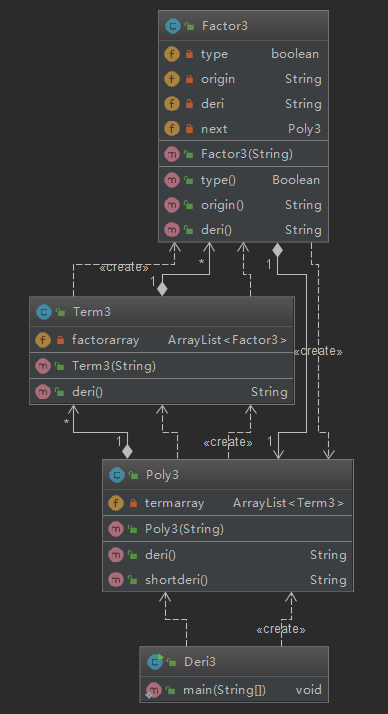
3.1.2基于度量的分析
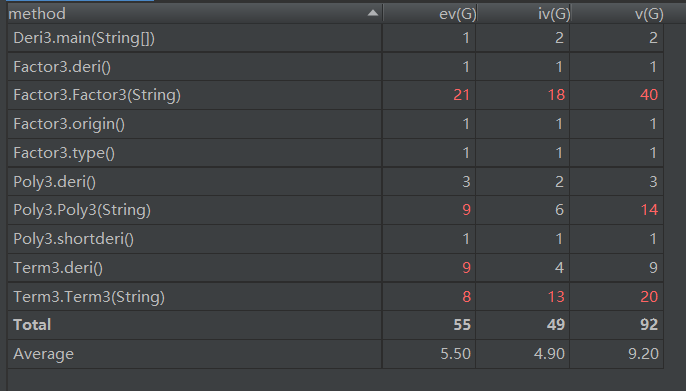
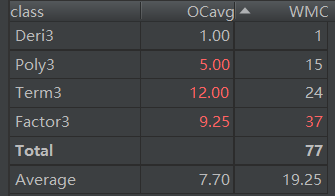
我对比了一下别人的代码复杂度,我第三次作业的复杂度算是炸了,可能是类太少,干得活太多.....除了Deri()类,其他类都挺辛苦的,我都不好意思分析了.....反正能者多劳吧,三个类都挺复杂的。好在这次不仅是构造函数比较辛苦,求导也复杂度比较高,一家人就应该整整齐齐。
2.2思考过程
第三次作业是最复杂的一次,也是我做得最简单的一次。大部分时间都花在了构思上,所以敲起代码反而得心应手。大正则的时代已经过去了,这次我选做了通过正负号来切分多项式,再通过乘号来切分因子。问题的难点在于括号的干扰,当然这对于大佬不是问题。我用了一个比较笨的办法,匹配到括号开始另一段正则匹配,数到相同数量的左右括号时再开始之前的加(乘)号匹配。对因子分情况求导,当因子是基础因子时(不含多项式)返回特定结果,因子不是特定因子时,对组成因子的多项式进行递归存储。这样存储以后,求导的时候就很简单,我们只需要把他的下一级看成一个整体,就可以很容易地表示出这一级的导函数,直到基础因子时,返回基础因子的导数。在返回导函数的同时,我还对系数,指数为0,和为1的情况在每一级进行化简,以减少递归时的计算压力。这样做的时候,输入格式判断也变简单了。只要上一级的输入,不满足这一层的接口,则抛出异常。可以看出,在整个计算过程中,我完全抛弃了int型(或BigInteger型)的变量,全部都是以String的形式进行传递,这样做简单粗暴,但是不利于最后的化简。不过对于我这样咸鱼玩家来说,也没有化简的必要了。
2.3制造bug的原因
对于输出结果,专门写了一个shortderi()方法,其中存在错误的化简。
没有仔细看指导书,无视了大整数,在factor类中错误地抛出异常。
4、总览
仔细看指导书会减少bug,减少因为“无知”产生的bug。
花时间放在构思上,比花时间放在修补上更值得。
二、分析bug的策略及问题
策略:
1、在自己写程序时,每注意到一个点,就写一个测试数据,到最后会有一个小规模的测试集,虽然这个测试集对于自己的程序没什么杀伤力,但对于别人的程序,可能是个不错的武器。
2、系统地构造wrong fromat的情况,尽可能排列出所有元素小于4个的组合
3、构造复杂的输入
4、脚本生成规范的输入,将输出结果与matlab自动比对
测bug的不足:
1、没有覆盖全面的format
2、没有覆盖全面的计算结果
PS:没有结合除自己以外被测者的代码设计结构构造样例。