原理
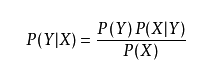
举例
假设:有360封电子邮件,其中:
正常邮件=240封,垃圾邮件=120封;
分词在邮件中出现次数如下:
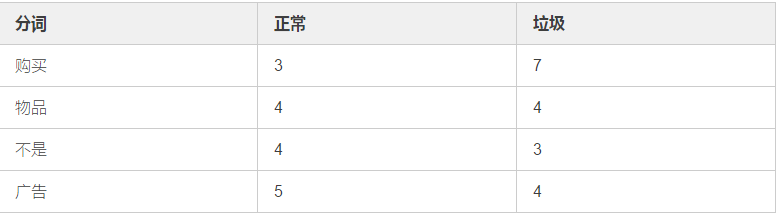
件内容), 则可以认为是垃圾邮件
如果P(垃圾|邮件内容) <= P(正常|邮件内容), 则可以认为是正常邮件
从上述统计结果中我们可以得出相应的概率值:
P(正常)=2/3
P(垃圾)=1/3
P("购买"|正常)=3/240=1/80
P("购买"|垃圾)=7/120
P("物品"|正常)=1/60
P("物品"|垃圾)=1/30
P("不是"|正常)=1/60
P("不是"|垃圾)=1/40
P("广告"|正常)=1/48
P("广告"|垃圾)=1/30
现有一封邮件内容为:
"购买物品,不是广告"
那么它是垃圾邮件么?
我们假设上述我们选择的分词之间是相互独立的,没有因果联系(朴素贝叶斯,如果不独立就不是朴素贝叶斯了)
那么有推论:

其实我们最终要比较的是:
P(正常|邮件内容)和P(垃圾|邮件内容)之间的大小。
经过化简也就是判断:
P("购买"|正常)P("物品"|正常)P("不是"|正常)P("广告"|正常)P(正常)和
P("购买"|垃圾)P("物品"|垃圾)P("不是"|垃圾)P("广告"|垃圾)P(垃圾)之间的大小。
计算结果:
约掉分母,显然:
3445 < 14868
因此,此邮件是一封垃圾邮件。
总结
由此推论步骤中,我们可以看出
模型中,各个分词(X)和标签y的概率是先给出的(先验的,训练数据)
我们预测所需要输入的是字典中的分词在需要验证的邮件中出现的结果。
实践
1. 对数据预处理
确定那些词是不需要统计的,比如非中文符号、表情、字符、数字、字母和一些不想统计的词"的"、"呢"、"了"之类的词。
将无法分类的词用特定的词替换掉;
获取不想统计的词库"stopwords";
处理文本,将不想统计的词库中的词删掉;
2. TF-IDF处理(获取数据特征,数据label)
TF-IDF(term-frequency,inverse doucument frequency )是一种统计方法,用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降
将预处理过的文本交给TF-IDF进行特征提取
tfidf = TfidfVectorizer()
X_train = tfidf.fit_transform(train_comments_new) # 训练数据的特征
y_train = train_labels # 训练数据的label
X_test = tfidf.transform(test_comments_new) # 测试数据的特征
y_test = test_labels# 测试数据的label
3. 用朴素贝叶斯进行训练和预测
clf = MultinomialNB()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print("accuracy on test data: ", accuracy_score(y_test, y_pred))