P2751 [USACO4.2]工序安排Job Processing
题目描述
一家工厂的流水线正在生产一种产品,这需要两种操作:操作A和操作B。每个操作只有一些机器能够完成。
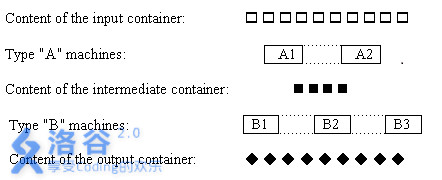
上图显示了按照下述方式工作的流水线的组织形式。A型机器从输入库接受工件,对其施加操作A,得到的中间产品存放在缓冲库。B型机器从缓冲库接受中间产品,对其施加操作B,得到的最终产品存放在输出库。所有的机器平行并且独立地工作,每个库的容量没有限制。每台机器的工作效率可能不同,一台机器完成一次操作需要一定的时间。
给出每台机器完成一次操作的时间,计算完成A操作的时间总和的最小值,和完成B操作的时间总和的最小值。
注:1、机器在一次操作中干掉一个工件; 2、时间总和的意思是最晚时间点
输入输出格式
输入格式:
第一行 三个用空格分开的整数:N,工件数量 (1<=N<=1000);M1,A型机器的数量 (1<=M1<=30);M2,B型机器的数量 (1<=M2<=30)。
第二行…等 M1个整数(表示A型机器完成一次操作的时间,1..20),接着是M2个整数(B型机器完成一次操作的时间,1..20)
输出格式:
只有一行。输出两个整数:完成所有A操作的时间总和的最小值,和完成所有B操作的时间总和的最小值(A操作必须在B操作之前完成)。
输入输出样例
输入样例:
5 2 3
1 1 3 1 4
输出样例:
3 5
贪心的题都很神啊。这题耗了我一晚上(我太蒻了)
首先第一问的方法似乎很多,我介绍一下我想的
策略:保证用完某个机器后时间最短
做法:从小到大枚举时间,时间每增加1,对每一个机器的可使用时间就增加1,当一个机器的可使用时间等于它单次操作的时间后,就做并清0
第二问的方法大体有两种,我只弄懂了一种
是一个转换的思想,我们把从B做的操作单独处理,然后用最小-最大进行配对。
具体做法是将B处理按A的方式同样处理,得到每个工件处理完成的时间,然后把A中最小和B中最大取配对并删除,答案即为最大配对值
还有一种大概是直接按时间在B中处理并且用堆维护,看不懂orz
总结:并行取配对,类似的题
Code:
#include <cstdio>
int max(int x,int y){return x>y?x:y;}
const int N=32;
int a[N],b[N],n,m1,m2,t1[N],t2[N],put0[1010],put1[1010];
int main()
{
scanf("%d%d%d",&n,&m1,&m2);
for(int i=1;i<=m1;i++)
scanf("%d",t1+i);
for(int i=1;i<=m2;i++)
scanf("%d",t2+i);
int t=0,cnt=n;
while(cnt)
{
t++;
for(int i=1;i<=m1;i++)
{
a[i]++;
if(a[i]==t1[i]) a[i]=0,put0[cnt--]=t;
if(!cnt) break;
}
}
printf("%d ",t);
t=0,cnt=n;
while(cnt)
{
t++;
for(int i=1;i<=m1;i++)
{
b[i]++;
if(b[i]==t2[i]) b[i]=0,put1[cnt--]=t;
if(!cnt) break;
}
}
int ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,put0[i]+put1[n+1-i]);
printf("%d
",ans);
return 0;
}
2018.7.10