连续子数组的最大和（python）

一，问题

在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，

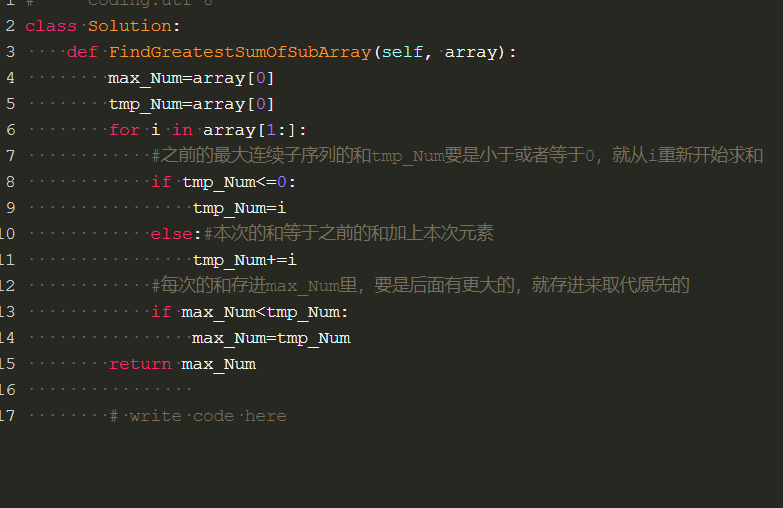
二，分析

先举个栗子

array={6,-3,-2,7,-15,1,2,2}

我先放两个盒子，里面装进array的第一个元素6

max_Num=array[0]=6
tmp_Num=array[0]=6

然后和后面的数字去求和，当出现求和的结果大于第一个元素6时，就替换6存进max_Num这个盒子里，之后如果有更大的，就再存进来

最大的连续子序列的和是由当前元素和 之前的最大连续子序列的和 叠加在一起形成的

如果之前的最大连续子序列的和大于零，我们可以继续累加，如果小于零，则需要舍去之前的子序列，重新从当前的数字开始累加。

i= - 3

tmp_Num=6-3=3

3<6所以max_Num还是6

i= - 2

tmp_Num=3-2=1

i= 7

tmp_Num=3+7=10

10>6所以max_Num=10

i=-15

tmp_Num=10-15=-5

i=1

此时tmp_Num=-5<0，所以tmp_Num=1

i=2

tmp_Num=1+2=3

i=2

tmp_Num=3+2=5

tmp_Num没有大于10的，所以输出max_Num=10

三，代码