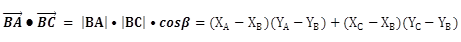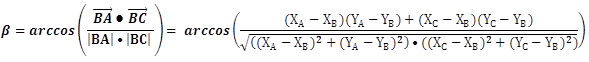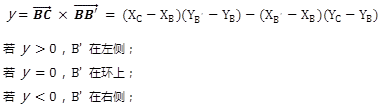前段时间有写过一个计算多边形角度的代码,这里给它整理整理,留给自己也送给萌新。
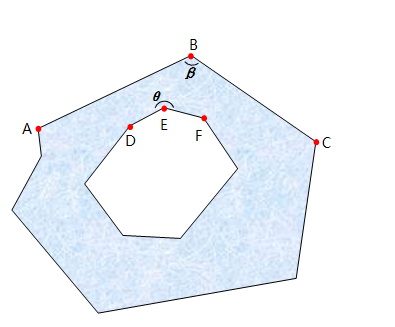
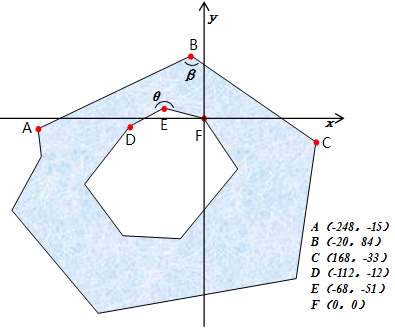
看左下图,这是一个多环的多边形,一个外环(内部为多边形内部区域),一个内环(外部为多边形内部区域),同时多边形中任意一个角不等于零角(等于 0° 的角)或周角(等于 360° 的角)。注意:本文下文所讨论的多边形求角度不包含零角和周角。
现在我们要求 ∠ABC 和 ∠DEF 的大小。那咋算唻?
1. 内积计算夹角
给它加上坐标系(坐标是自己配的,计算出的角度值不一定准确,但不影响角度大小的关系), 如右上图。角度采用向量的内积来求。
以上面的 ∠ABC 为例,数学计算公式如下。
于是乎,有:
角度计算代码如下:

public struct CxPoint { public CxPoint(double x, double y) { X = x; Y = y; } public double X; public double Y; } /// <summary> /// 计算三点角度,p1-p2-p3为沿环方向的三个连续顶点,其中p2为角点。计算结果范围 0° - 180°,-1为无效值 /// </summary> private static double CalculationAngle(CxPoint p1, CxPoint p2, CxPoint p3) { //Cos(Angle) = a•b/(|a|*|b|) double x1 = p1.X - p2.X, y1 = p1.Y - p2.Y; //向量 a double x2 = p3.X - p2.X, y2 = p3.Y - p2.Y; //向量 b //零向量,存在共点 if (x1 == 0 && y1 == 0) return -1; if (x2 == 0 && y2 == 0) return -1; double v = x1 * x2 + y1 * y2; //向量内积 a•b double val = Math.Sqrt((x1 * x1 + y1 * y1) * (x2 * x2 + y2 * y2)); //a,b模长乘积 |a|*|b| double CosAngle = v / val; //求出来的值可能略小于 -1 或者略大于 1,此时 Angle 等于 NaN double Angle = Math.Acos(CosAngle) * 180.0 / 3.14159265358979; //两向量夹角,0-180 if (System.Double.IsNaN(Angle)) { if (v > 0) return 0; else return 180; } else { if (Angle > 180) return 180; else if (Angle < 0) return 0; else return Angle; } }
用上述代码我们能够计算得出 ∠ABC = 124.63°,∠DEF = 101.57°。细心的朋友会发现,∠DEF 很明显是个优角(大于 180° 小于 360° 的角),为什么求出来是个劣角的值(大于 0° 小于 180° 的角)呢?原来反余弦函数的值域为 [ 0,π ],故采用向量内积计算出来的夹角总是在 [ 0°,180° ] 之间。
2. 外积判断互组
针对像 ∠DEF 这种优角,我们如何计算其结果呢?原来,内积计算的夹角与正确结果必定互为组角(相加等于 360° 的两个角互为组角),如此 ∠DEF 的正确结果为 360° - 101.57° = 258.43°。故在内积计算夹角后,问题转换为判别待求角是优角还是劣角,优角则求其组角,劣角则直接是结果。
以 ∠ABC 为例 ,A → B → C 为环方向,取AC中点M,再取 BM 上靠近 B 点的 B' 点(称为面内面外判断点),其中 BB' 的距离很小很小(若直接以 M 点作为面内面外判断点,由于存在多环的情况,会出现问题)。若 B' 在多边形内,则待求角为劣角,内积计算夹角即为结果,若 B' 在多边形外,即出现 ∠DEF 这种情况(此时 B' 是 E'),则需要求内积计算夹角的组角作为计算结果。
面内面外判断点求取代码如下:

/// <summary> /// 求取面内面外判断点,p1-p2-p3为沿环方向的三个连续顶点,其中p2为角点。 /// </summary> private static CxPoint CalculationJudgePoint(CxPoint p1, CxPoint p2, CxPoint p3, double SmallDis = 0.01) { double TempX = (p1.X + p3.X) / 2; double TempY = (p1.Y + p3.Y) / 2; double DisX = TempX - p2.X; double DisY = TempY - p2.Y; double val = Math.Sqrt(DisX * DisX + DisY * DisY); double Scale = SmallDis / val; return new CxPoint(p2.X + Scale * DisX, p2.Y + Scale * DisY); }
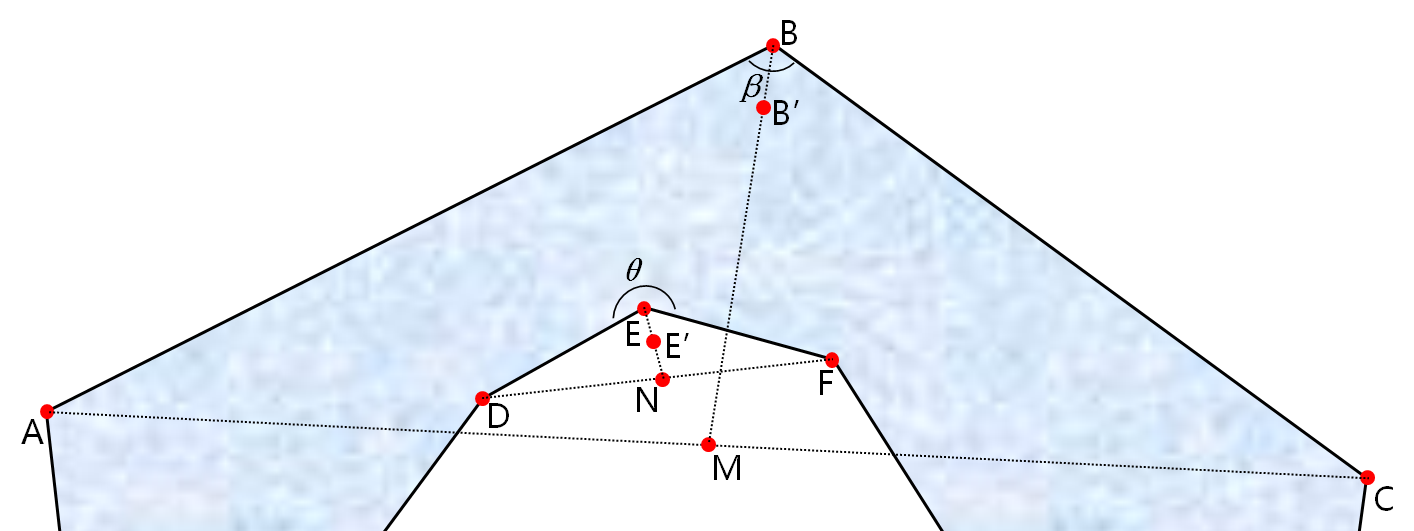
假设,沿着环的方向,多边形的内部总在环的右侧区域,所以在上图中,∠ABC 所在的环为顺时针方向,∠DEF 所在的环为逆时针方向。有了这个假设,我们就能够用向量外积来判断 B' (或者是 E')点是否在面内了。具体做法为计算 ( 待求角角点,沿环方向角点下一顶点 ) 与 ( 待求角角点,面内面外判断点 ) 的外积(在本文图中为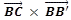 和
和  ):结果若大于 0,则面内面外判断点在环的左侧和多边形外部,待求角为优角,求内积计算夹角的组角作为结果;结果若小于等于 0,则面内面外判断点在环的右侧和多边形内部或边界上,待求角为劣角或平角,内积计算夹角直接作为结果。
):结果若大于 0,则面内面外判断点在环的左侧和多边形外部,待求角为优角,求内积计算夹角的组角作为结果;结果若小于等于 0,则面内面外判断点在环的右侧和多边形内部或边界上,待求角为劣角或平角,内积计算夹角直接作为结果。
以判断 B' 在 BC 的哪一侧为例,数学计算公式如下。
左右侧判断代码如下:

public struct CxLine { public CxLine(CxPoint fromPoint, CxPoint toPoint) { FromPoint = fromPoint; ToPoint = toPoint; } public CxPoint FromPoint; public CxPoint ToPoint; } /// <summary> /// 判断点在线的左方还是右方,在左为 true,在线上或在右为 false /// </summary> public static bool JudgAbout(CxLine pLine, CxPoint pPoint) { double ax = pLine.ToPoint.X - pLine.FromPoint.X; double ay = pLine.ToPoint.Y - pLine.FromPoint.Y; double bx = pPoint.X - pLine.FromPoint.X; double by = pPoint.Y - pLine.FromPoint.Y; double judge = ax * by - ay * bx; if (judge > 0.0) return true; else return false; }
3. 求角源码整理
通过上述分析,将所有代码整理成一个 cs 类。

/// <summary> /// 调用示例:AngleCalculation.CxPoint p1 = new AngleCalculation.CxPoint(-112, -12); /// AngleCalculation.CxPoint p2 = new AngleCalculation.CxPoint(-68, -51); /// AngleCalculation.CxPoint p3 = new AngleCalculation.CxPoint(0, 0); /// double angle = AngleCalculation.Analysis(p1, p2, p3, true); /// </summary> public sealed class AngleCalculation { public struct CxPoint { public CxPoint(double x, double y) { X = x; Y = y; } public double X; public double Y; } public struct CxLine { public CxLine(CxPoint fromPoint, CxPoint toPoint) { FromPoint = fromPoint; ToPoint = toPoint; } public CxPoint FromPoint; public CxPoint ToPoint; } /// <summary> /// 角度计算主方法,p1-p2-p3为沿环方向的三个连续顶点,其中p2为角点。 /// </summary> /// <param name="IsClockwise">p1-p2-p3所在环方向,顺时针为 true,逆时针为 false</param> public static double Analysis(CxPoint p1, CxPoint p2, CxPoint p3, bool IsClockwise) { double Angle = CalculationAngle(p1, p2, p3); if (Angle == -1) return Angle; CxPoint JudgePoint = CalculationJudgePoint(p1, p2, p3); CxLine ReferenceLine = new CxLine(p2, p3); bool IsLeft = JudgAbout(ReferenceLine, JudgePoint); if (IsClockwise == IsLeft) Angle = 360 - Angle; return Angle; } /// <summary> /// 计算三点角度,p1-p2-p3为沿环方向的三个连续顶点,其中p2为角点。计算结果范围 0° - 180°,-1为无效值 /// </summary> private static double CalculationAngle(CxPoint p1, CxPoint p2, CxPoint p3) { //Cos(Angle) = a•b/(|a|*|b|) double x1 = p1.X - p2.X, y1 = p1.Y - p2.Y; //向量 a double x2 = p3.X - p2.X, y2 = p3.Y - p2.Y; //向量 b //零向量,存在共点 if (x1 == 0 && y1 == 0) return -1; if (x2 == 0 && y2 == 0) return -1; double v = x1 * x2 + y1 * y2; //向量内积 a•b double val = Math.Sqrt((x1 * x1 + y1 * y1) * (x2 * x2 + y2 * y2)); //a,b模长乘积 |a|*|b| double CosAngle = v / val; //求出来的值可能略小于 -1 或者略大于 1,此时 Angle 等于 NaN double Angle = Math.Acos(CosAngle) * 180.0 / 3.14159265358979; //两向量夹角,0-180 if (System.Double.IsNaN(Angle)) { if (v > 0) return 0; else return 180; } else { if (Angle > 180) return 180; else if (Angle < 0) return 0; else return Angle; } } /// <summary> /// 求取面内面外判断点,p1-p2-p3为沿环方向的三个连续顶点,其中p2为角点。 /// </summary> private static CxPoint CalculationJudgePoint(CxPoint p1, CxPoint p2, CxPoint p3, double SmallDis = 0.01) { double TempX = (p1.X + p3.X) / 2; double TempY = (p1.Y + p3.Y) / 2; double DisX = TempX - p2.X; double DisY = TempY - p2.Y; double val = Math.Sqrt(DisX * DisX + DisY * DisY); double Scale = SmallDis / val; return new CxPoint(p2.X + Scale * DisX, p2.Y + Scale * DisY); } /// <summary> /// 判断点在线的左方还是右方,在左为 true,在线上或在右为 false /// </summary> private static bool JudgAbout(CxLine pLine, CxPoint pPoint) { double ax = pLine.ToPoint.X - pLine.FromPoint.X; double ay = pLine.ToPoint.Y - pLine.FromPoint.Y; double bx = pPoint.X - pLine.FromPoint.X; double by = pPoint.Y - pLine.FromPoint.Y; double judge = ax * by - ay * bx; if (judge > 0.0) return true; else return false; } } }
|
作者:喵...鱼...喵 出处:https://www.cnblogs.com/bwuwj/ 本文为作者原创,版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接,否则保留追究法律责任的权利。如本文有误,欢迎批评指正。 |