bzoj 4237: 稻草人 cdq分治

　　

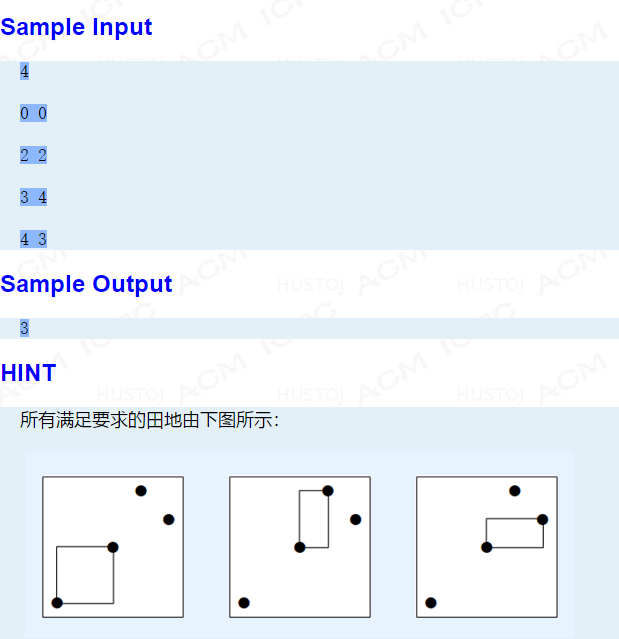
求有多少个点对  其一个点为左下角  一个点为右下角所形成的矩形内部没有点 每个x与y都不同

一开始的思路：

先按照x坐标排序  进行cdq分治  

然后在cdq内对y进行排序  枚举mid+1-r的点作为右上角的点

发现只要维护左半边的的单调递增就可以形成点对  用单调栈很好的维护

但是忽略了右半边已经遍历过的点对答案产生的影响

参考了yyb巨佬:https://www.cnblogs.com/cjyyb/p/8419102.ht

 想一下新增点的x左边可以发现影响关系

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i>=(b);--i)
#define ll long long
#define see(x) (cerr<<(#x)<<'='<<(x)<<endl)
#define inf 0x3f3f3f3f
#define CLR(A,v)  memset(A,v,sizeof A)
/////////////////////////////////////
const int N=1e6+10;
//维护单调递减的单调栈
int n,m;ll ans[N];ll sum;
struct node{int x,y,id;}s[N];
bool cmp(node a,node b){return a.y>b.y;}
bool cmpx(node a,node b){return a.x<b.x;}
int sta1[N],top1,sta2[N],top2;

void cdq(int l,int r)
{
    if(l==r)return ;int mid=(l+r)>>1;
    cdq(l,mid);cdq(mid+1,r);
    int j=mid+1;
    sort(s+l,s+mid+1,cmp);sort(s+mid+1,s+r+1,cmp);
    int top1=top2=0;
    rep(i,l,mid)
    {
        while(j<=r&&s[i].y<s[j].y)
        {
            while(top1>0&&s[sta1[top1]].x>s[j].x)top1--;
            sta1[++top1]=j++;
        }
        while(top2>0&&s[sta2[top2]].x<s[i].x)top2--;
        sta2[++top2]=i;
        if(top2==1)sum+=1ll*top1;
        else 
        {
            int L=1,R=top1,an=top1+1;
            while(L<=R)
            {
                int mid=(L+R)>>1;
                if(s[sta1[mid]].y>s[sta2[top2-1]].y)L=mid+1;
                else an=mid,R=mid-1;
            }
            sum+=1ll*top1-an+1;
        }
    }
}
int main()
{
    cin>>n;
    rep(i,1,n)
    {
        scanf("%d%d",&s[i].x,&s[i].y);s[i].id=i;
    }
    sort(s+1,s+1+n,cmpx);
    cdq(1,n);
    cout<<sum;
    return 0;
}