D. Marcin and Training Camp
题意: 每个人有两个属性ai bi bi表示这个人的能力值 ai的二进制表示为这个人会哪几种技能
当b会某种技能而a不会的时候 那么a佩服b 所以也可以互相佩服
需要组建一个团队 至少两个人 要求团队中不存在一个人没有佩服的对象 问团队的最大能力值
如果团队中一个人的能力值不被其他一个人的能力值所完全碾压的话 那么肯定组不成团队
这样的话就可以一路往强的人走 那么最强的ai 肯定不止一个人 否则组不成团队
那么就可以枚举所有的超过一个人的ai 累和所有的bi即可

#include<bits/stdc++.h> using namespace std; #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define ll long long #define see(x) (cerr<<(#x)<<'='<<(x)<<endl) #define inf 0x3f3f3f3f #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// const int N=2e6+10; ll ans; ll a[N],b[N]; map<ll,ll>mp,mp2,vis; vector<ll>t; int main() { int n; cin>>n; rep(i,1,n)scanf("%lld",&a[i]); rep(i,1,n)scanf("%lld",&b[i]); rep(i,1,n) { mp2[a[i]]++; if(mp2[a[i]]==1)t.push_back(a[i]); mp[a[i]]+=b[i]; } for(auto i:t) { if(mp2[i]<2||vis[i])continue; vis[i]=1; ans+=mp[i]; for(auto j:t) { if(vis[j])continue; if( (i|j)==i )vis[j]=1,ans+=mp[j]; } } cout<<ans; return 0; }
E. Kamil and Making a Stream
题意:一棵以1为根节点点权树 问每个点与其到根节点路径上的点对(包括自己)的路径gcd之和
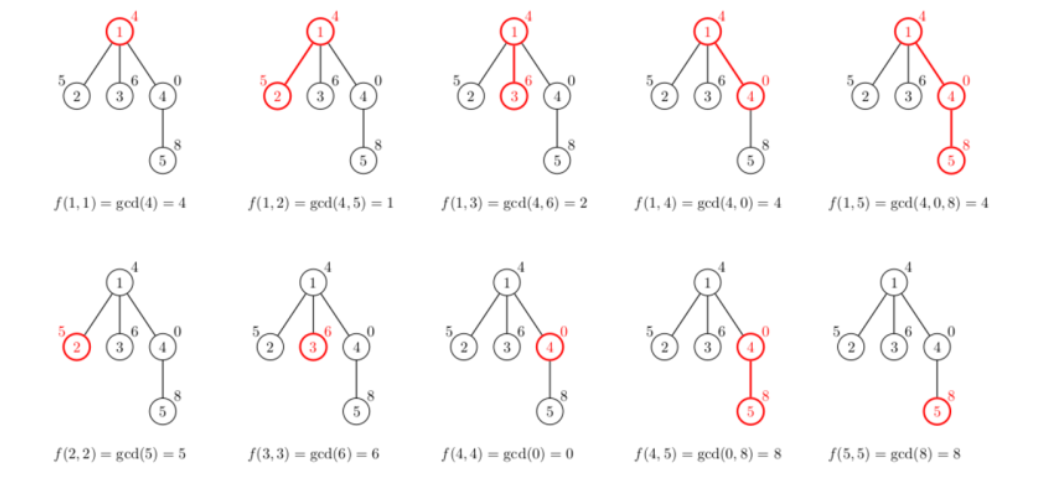
第一眼看起来很像是点分治 但是明显不行 点分治是任意点对
dfs一路继承x节点的所有gcd 转移到v节点的时候 只要和x节点的gcd遍历一遍即可 显然gcd数量不会很多

#include<bits/stdc++.h> using namespace std; #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define ll long long #define see(x) (cerr<<(#x)<<'='<<(x)<<endl) #define inf 0x3f3f3f3f #define CLR(A,v) memset(A,v,sizeof A) ///////////////////////////////////// const int N=1e5+10; const ll mod=1e9+7; int n; vector<int>edge[N]; ll ans,x[N]; map<ll,ll>mp[N]; void dfs(int u,int fa) { mp[u][x[u]]+=1; ans+=x[u]; for(auto v:mp[fa]) { ll g=__gcd(v.first,x[u]); ans=(ans + g*v.second ) % mod; mp[u][g]+=v.second; } for(auto v:edge[u])if(v!=fa) dfs(v,u); } int main() { cin>>n; rep(i,1,n)scanf("%lld",&x[i]); int u,v; rep(i,1,n-1)scanf("%d%d",&u,&v),edge[u].push_back(v),edge[v].push_back(u); dfs(1,0); cout<<ans; return 0; }
F. Konrad and Company Evaluation
题意:一个有向图有n个点m条边 每条边从编号大的点指向编号小的点 有q个操作 每次将一个点的编号变为最大 也就是将x点的所有边全部变为被指向 每次输出当前图有多少个三元关系 满足 a指向b b指向c


非常好的思维题!
首先考虑建图:
因为每次对一个点进行操作的时候 显然要更新图 假设y本来指向x 当更新x的时候 y指向x的edge要被删去 如果遍历y的边肯定是会t
可以考虑反向建图 那么对x操作的时候只只需要给加边 然后将x的边清空即可 避免了删除操作 !!!
所以问题就可以转化为指向大的点 每次操作将一个点 变为最小的点
然后枚举一下情况就可以了

#include<bits/stdc++.h> using namespace std; #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define ll long long #define see(x) (cerr<<(#x)<<'='<<(x)<<endl) #define inf 0x3f3f3f3f #define CLR(A,v) memset(A,v,sizeof A) ///////////////////////////////////// const int N=1e5+10; const ll mod=1e9+7; vector<int>edge[N]; int n,m,q,x,u,v,d[N]; ll ans,res[N]; int main() { cin>>n>>m; rep(i,1,m) { scanf("%d%d",&u,&v); if(u>v)swap(u,v); d[u]++;d[v]++; edge[u].push_back(v); } rep(i,1,n) { ll temp=edge[i].size(); res[i]=temp*(d[i]-temp);//当前点作为中间点的答案为入度乘出度 ans+=res[i]; } cout<<ans<<endl; cin>>q; while(q--) { scanf("%d",&x); ans-=res[x];//作为中间点的情况不存在了 res[x]=0; for(auto v:edge[x]) { res[v]-=edge[v].size(); ans-=edge[v].size();//减去v点作为中间点的情况 ll temp= d[v]-1-edge[v].size() ; res[v]+=temp; ans+=temp; edge[v].push_back(x); } edge[x].clear(); printf("%lld ",ans); } return 0; }
