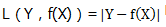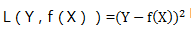前言:损失函数是机器学习里最基础也是最为关键的一个要素,通过对损失函数的定义、优化,就可以衍生到我们现在常用的机器学习等算法中
损失函数的作用:衡量模型模型预测的好坏。
正文:
首先我们假设要预测一个公司某商品的销售量:
X:门店数 Y:销量
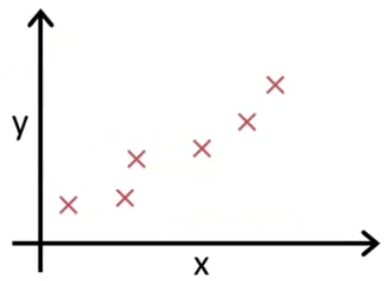
我们会发现销量随着门店数上升而上升。于是我们就想要知道大概门店和销量的关系是怎么样的呢?
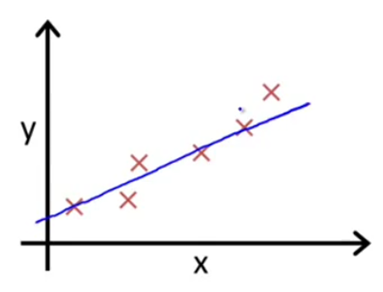
我们根据图上的点描述出一条直线:
似乎这个直线差不多能说明门店数X和Y得关系了:我们假设直线的方程为Y=a0+a1X(a为常数系数)。假设a0=10 a1=3 那么Y=10+3X(公式1)
|
X |
公式Y |
实际Y |
差值 |
|
1 |
13 |
13 |
0 |
|
2 |
16 |
14 |
2 |
|
3 |
19 |
20 |
-1 |
|
4 |
22 |
21 |
1 |
|
5 |
25 |
25 |
0 |
|
6 |
28 |
30 |
-2 |
我们希望我们预测的公式与实际值差值越小越好,所以就定义了一种衡量模型好坏的方式,即损失函数(用来表现预测与实际数据的差距程度)。于是乎我们就会想到这个方程的损失函数可以用绝对损失函数表示:
公式Y-实际Y的绝对值,数学表达式:
上面的案例它的绝对损失函数求和计算求得为:6
为后续数学计算方便,我们通常使用平方损失函数代替绝对损失函数:
公式Y-实际Y的平方,数学表达式:L(Y,f(X))=
上面的案例它的平方损失函数求和计算求得为:10
以上为公式1模型的损失值。
假设我们再模拟一条新的直线:a0=8,a1=4
|
X |
公式Y |
实际Y |
差值 |
|
1 |
12 |
13 |
-1 |
|
2 |
16 |
14 |
2 |
|
3 |
20 |
20 |
0 |
|
4 |
24 |
21 |
3 |
|
5 |
28 |
25 |
3 |
|
6 |
32 |
30 |
2 |
公式对比,学习损失函数的意义
公式2 Y=8+4X
绝对损失函数求和:11 平方损失函数求和:27
公式1 Y=10+3X
绝对损失函数求和:6 平方损失函数求和:10
从损失函数求和中,就能评估出公式1能够更好得预测门店销售。
统计学习中常用的损失函数有以下几种:
(1) 0-1损失函数(0-1 lossfunction):
(2) 平方损失函数(quadraticloss function)
(3) 绝对损失函数(absoluteloss function)
(4) 对数损失函数(logarithmicloss function)或对数似然损失函数(log-likelihood loss function)
损失函数越小,模型就越好。
总结:
损失函数可以很好得反映模型与实际数据差距的工具,理解损失函数能够更好得对后续优化工具(梯度下降等)进行分析与理解。很多时候遇到复杂的问题,其实最难的一关是如何写出损失函数。