数学优化

数学优化（Mathematical Optimization）问题，也叫最优化问题，是指在一定约束条件下，求解一个目标函数的最大值（或最小值）问题。

数学优化问题的定义为：给定一个目标函数（也叫代价函数）f : A → R，寻找一个变量（也叫参数）x^∗ ∈ D，使得对于所有D中的x，f(x^∗) ≤ f(x)（最小化）；或者f(x^∗) ≥ f(x)（最大化），其中D为变量x 的约束集，也叫可行域；D中的变量被称为是可行解。

 最优化问题一般可以表示为求最小值问题。求f(x) 最大值等价于求−f(x) 的最小值。

数学优化的类型

离散优化问题

离散优化（Discrete Optimization）问题是目标函数的输入变量为离散变量，比如为整数或有限集合中的元素。离散优化问题的求解一般都比较困难，优化算法的复杂度都比较高。离散优化问题主要有两个分支：

　　1. 组合优化（Combinatorial Optimization）：其目标是从一个有限集合中找出使得目标函数最优的元素。在一般的组合优化问题中，集合中的元素之间存在一定的关联，可以表示为图结构。典型的组合优化问题有旅行商问题、最小生成树问题、图着色问题等。很多机器学习问题都是组合优化问题，比如特征选择、聚类问题、超参数优化问题以及结构化学习（Structured Learning）中标签预测问题等。

　　2. 整数规划（Integer Programming）：输入变量x ∈ Z^d 为整数。一般常见的整数规划问题为整数线性规划（Integer Linear Programming，ILP）。整数线性规划的一种最直接的求解方法是：

　　　　（1）去掉输入必须为整数的限制，将原问题转换为一般的线性规划问题，这个线性规划问题为原问题的松弛问题；

　　　　（2）求得相应松弛问题的解；

　　　　（3）把松弛问题的解四舍五入到最接近的整数。但是这种方法得到的解一般都不是最优的，因此原问题的最优解不一定在松弛问题最优解的附近。另外，这种方法得到的解也不一定满足约束条件。

连续优化问题

连续优化（Continuous Optimization）问题是目标函数的输入变量为连续变量x ∈ R^d，即目标函数为实函数。

无约束优化和约束优化

在连续优化问题中，根据是否有变量的约束条件，可以将优化问题分为无约束优化问题和约束优化问题。

　　无约束优化问题：可行域为整个实数域D = R^d，可以写为

　　其中x ∈ R^d 为输入变量，f : R^d → R为目标函数。

　　约束优化问题：变量x需要满足一些等式或不等式的约束。约束优化问题通常使用拉格朗日乘数法来进行求解。

线性优化和非线性优化

如果在公式(C.1) 中，目标函数和所有的约束函数都为线性函数，则该问题为线性规划问题（Linear Programming）。相反，如果目标函数或任何一个约束函数为非线性函数，则该问题为非线性规划问题（Nonlinear Programming）

在非线性优化问题中，有一类比较特殊的问题是凸优化问题（Convex Programming）。在凸优化问题中，变量x 的可行域为凸集，即对于集合中任意两点，它们的连线全部位于在集合内部。目标函数f 也必须为凸函数，即满足

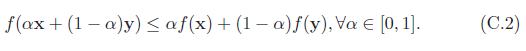
凸优化问题是一种特殊的约束优化问题，需满足目标函数为凸函数，并且等式约束函数为线性函数，不等式约束函数为凹函数。

优化算法

优化问题一般都是通过迭代的方式来求解：通过猜测一个初始的估计x₀，然后不断迭代产生新的估计x₁, x₂, · · · x_t，希望x_t 最终收敛到期望的最优解x^∗。一个好的优化算法应该是在一定的时间或空间复杂度下能够快速准确地找到最优解。同时，好的优化算法受初始猜测点的影响较小，通过迭代能稳定地找到最优解x^∗ 的邻域，然后迅速收敛于x^∗。

优化算法中常用的迭代方法有线性搜索和置信域方法等。线性搜索的策略是寻找方向和步长，具体算法有梯度下降法、牛顿法、共轭梯度法等。

全局最优和局部最优

对于很多非线性优化问题，会存在若干个局部的极小值。局部最小值，或局部最优解x^∗ 定义为：存在一个δ > 0，对于所有的满足∥x−x^∗∥ ≤ δ 的x，公式f(x^∗) ≤ f(x) 成立。也就是说，在x^∗ 的附近区域内，所有的函数值都大于或者等于f(x^∗)。

对于所有的x ∈ A，都有f(x^∗) ≤ f(x) 成立，则x^∗ 为全局最小值，或全局最优解（像loss一样，loss最小）。

一般的，求局部最优解是容易的，但很难保证其为全局最优解。对于线性规划或凸优化问题，局部最优解就是全局最优解。

要确认一个点x^∗ 是否为局部最优解，通过比较它的邻域内有没有更小的函数值是不现实的。如果函数f(x) 是二次连续可微（连续的二阶导数）的，我们可以通过检查目标函数在点x^∗ 的梯度∇f(x^∗) 和Hessian 矩阵∇²f(x^∗) 来判断。

　　

局部最小值的一阶必要条件： 如果x^∗ 为局部最优解并且函数f 在x^∗ 的邻域内一阶可微，则在∇f(x^∗) = 0。

证明：如果函数f(x) 是连续可微的，根据泰勒展开公式（Taylor’s Formula），函数f(x) 的一阶展开可以近似为

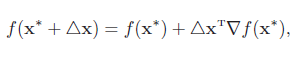
注：在这里可以将x*看做是x₀，△x看做是x-x_0，对照Taylaor展开式。

假设∇f(x^∗) ̸= 0，则可以找到一个△x（比如△x = −α∇f(x^∗)，α为很小的正数），使得

这和局部最优的定义矛盾。

注：为什么要选a为正数，因为采用了反证法，找到了一个反例，那么这个就不成立

局部最优解的二阶必要条件： 如果x^∗ 为局部最优解并且函数f 在x^∗ 的邻域内二阶可微，则在∇f(x^∗) = 0，∇2f(x^∗)为半正定矩阵。

证明：如果函数f(x) 是二次连续可微的，函数f(x) 的二阶展开可以近似为

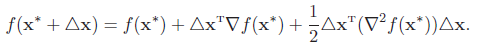
由一阶必要性定理可知∇f(x^∗) = 0，则

　

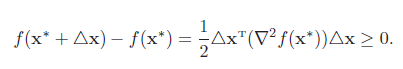
即∇²f(x^∗) 为半正定矩阵。

梯度下降法

梯度下降法（Gradient Descent Method），也叫最速下降法（Steepest Descend Method），经常用来求解无约束优化（可实行域为整个实数域）的极小值问题。

对于函数f(x)，如果f(x) 在点xt 附近是连续可微的，那么f(x) 下降最快的方向是f(x) 在xt 点的梯度方向的反方向。

根据泰勒一阶展开公式，

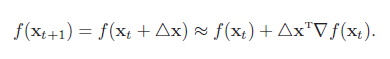
要使得f(x_t+1) < f(x_t)，就得使△x^T∇f(x_t) < 0。我们取△x = −α∇f(x_t)。如果α > 0 为一个够小数值时，那么f(x_t+1) < f(x_t) 成立。

这样我们就可以从一个初始值x₀ 出发，通过迭代公式

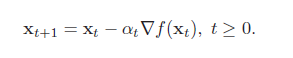
生成序列x₀, x₁, x₂, . . . 使得

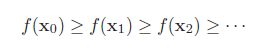
如果顺利的话，序列(x_n) 收敛到局部最优解x^∗。注意每次迭代步长α 可以改变，但其取值必须合适，如果过大就不会收敛，如果过小则收敛速度太慢。

梯度下降法为一阶收敛算法，当靠近极小值时梯度变小，收敛速度会变慢，并且可能以“之字形”的方式下降。如果目标函数为二阶连续可微，我们可以采用牛顿法。牛顿法为二阶收敛算法，收敛速度更快，但是每次迭代需要计算Hessian 矩阵的逆矩阵，复杂度较高。