Spark GraphX - 走看看

zoukankan html css js c++ java

Spark GraphX
1、GraphX介绍
 1.1 GraphX应用背景
Spark GraphX是一个分布式图处理框架，它是基于Spark平台提供对图计算和图挖掘简洁易用的而丰富的接口，极大的方便了对分布式图处理的需求。
众所周知·，社交网络中人与人之间有很多关系链，例如Twitter、Facebook、微博和微信等，这些都是大数据产生的地方都需要图计算，现在的图处理基本都是分布式的图处理，而并非单机处理。Spark GraphX由于底层是基于Spark来处理的，所以天然就是一个分布式的图处理系统。
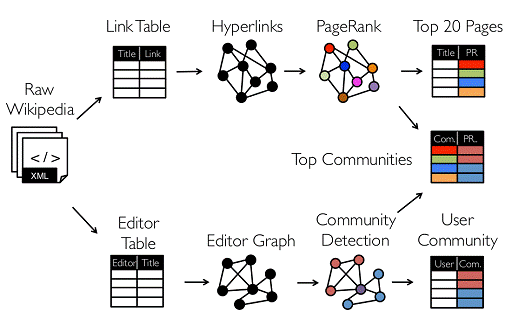
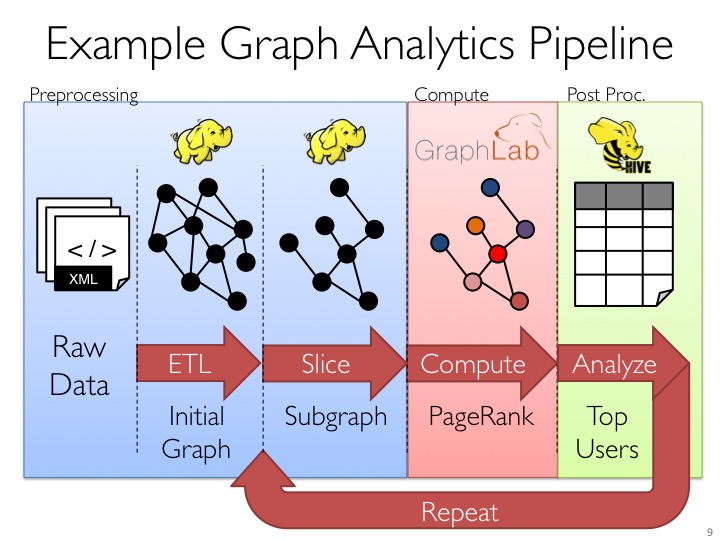
图的分布式或者并行处理其实是把图拆分成很多的子图，然后分别对这些子图进行计算，计算的时候可以分别迭代进行分阶段的计算，即对图进行并行计算。下面我们看一下图计算的简单示例：
从图中我们可以看出：拿到Wikipedia的文档以后，可以变成Link Table形式的视图，然后基于Link Table形式的视图可以分析成Hyperlinks超链接，最后我们可以使用PageRank去分析得出Top Communities。在下面路径中的Editor Graph到Community，这个过程可以称之为Triangle Computation，这是计算三角形的一个算法，基于此会发现一个社区。从上面的分析中我们可以发现图计算有很多的做法和算法，同时也发现图和表格可以做互相的转换。
1.2  GraphX的框架
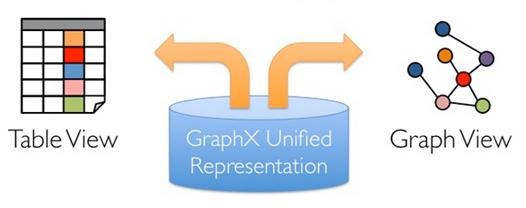
设计GraphX时，点分割和GAS都已成熟，在设计和编码中针对它们进行了优化，并在功能和性能之间寻找最佳的平衡点。如同Spark本身，每个子模块都有一个核心抽象。GraphX的核心抽象是Resilient Distributed Property Graph，一种点和边都带属性的有向多重图。它扩展了Spark RDD的抽象，有Table和Graph两种视图，而只需要一份物理存储。两种视图都有自己独有的操作符，从而获得了灵活操作和执行效率。
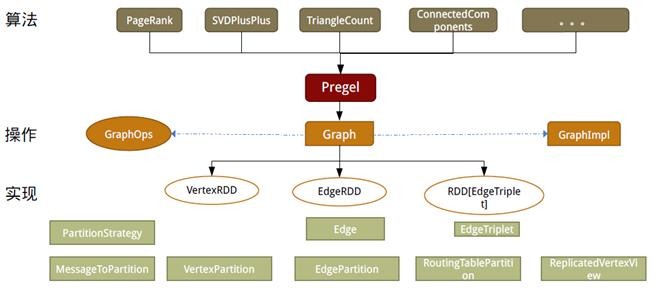
如同Spark，GraphX的代码非常简洁。GraphX的核心代码只有3千多行，而在此之上实现的Pregel模式，只要短短的20多行。GraphX的代码结构整体下图所示，其中大部分的实现，都是围绕Partition的优化进行的。这在某种程度上说明了点分割的存储和相应的计算优化，的确是图计算框架的重点和难点。
1.3 发展历程
l早在0.5版本，Spark就带了一个小型的Bagel模块，提供了类似Pregel的功能。当然，这个版本还非常原始，性能和功能都比较弱，属于实验型产品。
l到0.8版本时，鉴于业界对分布式图计算的需求日益见涨，Spark开始独立一个分支Graphx-Branch，作为独立的图计算模块，借鉴GraphLab，开始设计开发GraphX。
l在0.9版本中，这个模块被正式集成到主干，虽然是Alpha版本，但已可以试用，小面包圈Bagel告别舞台。1.0版本，GraphX正式投入生产使用。
值得注意的是，GraphX目前依然处于快速发展中，从0.8的分支到0.9和1.0，每个版本代码都有不少的改进和重构。根据观察，在没有改任何代码逻辑和运行环境，只是升级版本、切换接口和重新编译的情况下，每个版本有10%~20%的性能提升。虽然和GraphLab的性能还有一定差距，但凭借Spark整体上的一体化流水线处理，社区热烈的活跃度及快速改进速度，GraphX具有强大的竞争力。
2、GraphX实现分析
如同Spark本身，每个子模块都有一个核心抽象。GraphX的核心抽象是Resilient Distributed Property Graph，一种点和边都带属性的有向多重图。它扩展了Spark RDD的抽象，有Table和Graph两种视图，而只需要一份物理存储。两种视图都有自己独有的操作符，从而获得了灵活操作和执行效率。
GraphX的底层设计有以下几个关键点。
对Graph视图的所有操作，最终都会转换成其关联的Table视图的RDD操作来完成。这样对一个图的计算，最终在逻辑上，等价于一系列RDD的转换过程。因此，Graph最终具备了RDD的3个关键特性：Immutable、Distributed和Fault-Tolerant，其中最关键的是Immutable（不变性）。逻辑上，所有图的转换和操作都产生了一个新图；物理上，GraphX会有一定程度的不变顶点和边的复用优化，对用户透明。
两种视图底层共用的物理数据，由RDD[Vertex-Partition]和RDD[EdgePartition]这两个RDD组成。点和边实际都不是以表Collection[tuple]的形式存储的，而是由VertexPartition/EdgePartition在内部存储一个带索引结构的分片数据块，以加速不同视图下的遍历速度。不变的索引结构在RDD转换过程中是共用的，降低了计算和存储开销。
图的分布式存储采用点分割模式，而且使用partitionBy方法，由用户指定不同的划分策略（PartitionStrategy）。划分策略会将边分配到各个EdgePartition，顶点Master分配到各个VertexPartition，EdgePartition也会缓存本地边关联点的Ghost副本。划分策略的不同会影响到所需要缓存的Ghost副本数量，以及每个EdgePartition分配的边的均衡程度，需要根据图的结构特征选取最佳策略。目前有EdgePartition2d、EdgePartition1d、RandomVertexCut和CanonicalRandomVertexCut这四种策略。
2.1 存储模式
 2.1.1 图存储模式
巨型图的存储总体上有边分割和点分割两种存储方式。2013年，GraphLab2.0将其存储方式由边分割变为点分割，在性能上取得重大提升，目前基本上被业界广泛接受并使用。
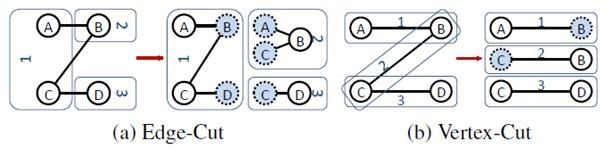
l边分割（Edge-Cut）：每个顶点都存储一次，但有的边会被打断分到两台机器上。这样做的好处是节省存储空间；坏处是对图进行基于边的计算时，对于一条两个顶点被分到不同机器上的边来说，要跨机器通信传输数据，内网通信流量大。
l点分割（Vertex-Cut）：每条边只存储一次，都只会出现在一台机器上。邻居多的点会被复制到多台机器上，增加了存储开销，同时会引发数据同步问题。好处是可以大幅减少内网通信量。
虽然两种方法互有利弊，但现在是点分割占上风，各种分布式图计算框架都将自己底层的存储形式变成了点分割。主要原因有以下两个。
1.磁盘价格下降，存储空间不再是问题，而内网的通信资源没有突破性进展，集群计算时内网带宽是宝贵的，时间比磁盘更珍贵。这点就类似于常见的空间换时间的策略。
2.在当前的应用场景中，绝大多数网络都是“无尺度网络”，遵循幂律分布，不同点的邻居数量相差非常悬殊。而边分割会使那些多邻居的点所相连的边大多数被分到不同的机器上，这样的数据分布会使得内网带宽更加捉襟见肘，于是边分割存储方式被渐渐抛弃了。
2.1.2 GraphX存储模式
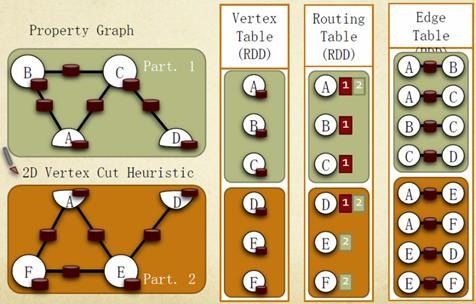
Graphx借鉴PowerGraph，使用的是Vertex-Cut(点分割)方式存储图，用三个RDD存储图数据信息：
lVertexTable(id, data)：id为Vertex id，data为Edge data
lEdgeTable(pid, src, dst, data)：pid为Partion id，src为原定点id，dst为目的顶点id
lRoutingTable(id, pid)：id为Vertex id，pid为Partion id
点分割存储实现如下图所示：
2.2 计算模式
 2.2.1 图计算模式
目前基于图的并行计算框架已经有很多，比如来自Google的Pregel、来自Apache开源的图计算框架Giraph/HAMA以及最为著名的GraphLab，其中Pregel、HAMA和Giraph都是非常类似的，都是基于BSP（Bulk Synchronous Parallell）模式。
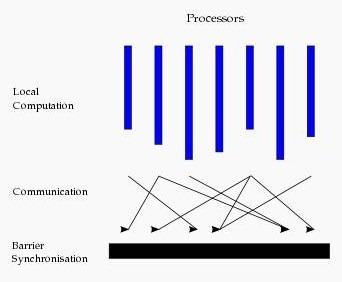
Bulk Synchronous Parallell，即整体同步并行，它将计算分成一系列的超步（superstep）的迭代（iteration）。从纵向上看，它是一个串行模式，而从横向上看，它是一个并行的模式，每两个superstep之间设置一个栅栏（barrier），即整体同步点，确定所有并行的计算都完成后再启动下一轮superstep。
每一个超步（superstep）包含三部分内容：
1.计算compute：每一个processor利用上一个superstep传过来的消息和本地的数据进行本地计算；
2.消息传递：每一个processor计算完毕后，将消息传递个与之关联的其它processors
3.整体同步点：用于整体同步，确定所有的计算和消息传递都进行完毕后，进入下一个superstep。
2.2.2GraphX计算模式
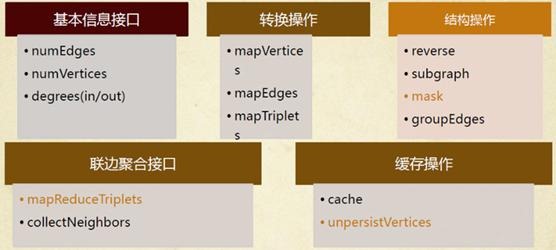
如同Spark一样，GraphX的Graph类提供了丰富的图运算符，大致结构如下图所示。可以在官方GraphX Programming Guide中找到每个函数的详细说明，本文仅讲述几个需要注意的方法。
2.2.2.1 图的缓存
每个图是由3个RDD组成，所以会占用更多的内存。相应图的cache、unpersist和checkpoint，更需要注意使用技巧。出于最大限度复用边的理念，GraphX的默认接口只提供了unpersistVertices方法。如果要释放边，调用g.edges.unpersist()方法才行，这给用户带来了一定的不便，但为GraphX的优化提供了便利和空间。参考GraphX的Pregel代码，对一个大图，目前最佳的实践是：
大体之意是根据GraphX中Graph的不变性，对g做操作并赋回给g之后，g已不是原来的g了，而且会在下一轮迭代使用，所以必须cache。另外，必须先用prevG保留住对原来图的引用，并在新图产生后，快速将旧图彻底释放掉。否则，十几轮迭代后，会有内存泄漏问题，很快耗光作业缓存空间。
2.2.2.2 邻边聚合
mrTriplets（mapReduceTriplets）是GraphX中最核心的一个接口。Pregel也基于它而来，所以对它的优化能很大程度上影响整个GraphX的性能。mrTriplets运算符的简化定义是：
它的计算过程为：map，应用于每一个Triplet上，生成一个或者多个消息，消息以Triplet关联的两个顶点中的任意一个或两个为目标顶点；reduce，应用于每一个Vertex上，将发送给每一个顶点的消息合并起来。
mrTriplets最后返回的是一个VertexRDD[A]，包含每一个顶点聚合之后的消息（类型为A），没有接收到消息的顶点不会包含在返回的VertexRDD中。
在最近的版本中，GraphX针对它进行了一些优化，对于Pregel以及所有上层算法工具包的性能都有重大影响。主要包括以下几点。
1. Caching for Iterative mrTriplets & Incremental Updates for Iterative mrTriplets：在很多图分析算法中，不同点的收敛速度变化很大。在迭代后期，只有很少的点会有更新。因此，对于没有更新的点，下一次mrTriplets计算时EdgeRDD无需更新相应点值的本地缓存，大幅降低了通信开销。
2.Indexing Active Edges：没有更新的顶点在下一轮迭代时不需要向邻居重新发送消息。因此，mrTriplets遍历边时，如果一条边的邻居点值在上一轮迭代时没有更新，则直接跳过，避免了大量无用的计算和通信。
3.Join Elimination：Triplet是由一条边和其两个邻居点组成的三元组，操作Triplet的map函数常常只需访问其两个邻居点值中的一个。例如，在PageRank计算中，一个点值的更新只与其源顶点的值有关，而与其所指向的目的顶点的值无关。那么在mrTriplets计算中，就不需要VertexRDD和EdgeRDD的3-way join，而只需要2-way join。
所有这些优化使GraphX的性能逐渐逼近GraphLab。虽然还有一定差距，但一体化的流水线服务和丰富的编程接口，可以弥补性能的微小差距。
2.2.2.3 进化的Pregel模式
GraphX中的Pregel接口，并不严格遵循Pregel模式，它是一个参考GAS改进的Pregel模式。定义如下：
这种基于mrTrilets方法的Pregel模式，与标准Pregel的最大区别是，它的第2段参数体接收的是3个函数参数，而不接收messageList。它不会在单个顶点上进行消息遍历，而是将顶点的多个Ghost副本收到的消息聚合后，发送给Master副本，再使用vprog函数来更新点值。消息的接收和发送都被自动并行化处理，无需担心超级节点的问题。
常见的代码模板如下所示：
可以看到，GraphX设计这个模式的用意。它综合了Pregel和GAS两者的优点，即接口相对简单，又保证性能，可以应对点分割的图存储模式，胜任符合幂律分布的自然图的大型计算。另外，值得注意的是，官方的Pregel版本是最简单的一个版本。对于复杂的业务场景，根据这个版本扩展一个定制的Pregel是很常见的做法。
2.2.2.4 图算法工具包
GraphX也提供了一套图算法工具包，方便用户对图进行分析。目前最新版本已支持PageRank、数三角形、最大连通图和最短路径等6种经典的图算法。这些算法的代码实现，目的和重点在于通用性。如果要获得最佳性能，可以参考其实现进行修改和扩展满足业务需求。另外，研读这些代码，也是理解GraphX编程最佳实践的好方法。
3、GraphX实例
 3.1  图例演示
 3.1.1 例子介绍
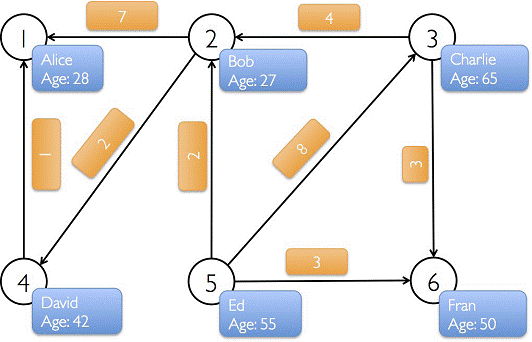
下图中有6个人，每个人有名字和年龄，这些人根据社会关系形成8条边，每条边有其属性。在以下例子演示中将构建顶点、边和图，打印图的属性、转换操作、结构操作、连接操作、聚合操作，并结合实际要求进行演示。
3.1.2 程序代码
import org.apache.log4j.{Level, Logger}
import org.apache.spark.{SparkContext, SparkConf}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
object GraphXExample {
  def main(args: Array[String]) {
    //屏蔽日志
    Logger.getLogger("org.apache.spark").setLevel(Level.WARN)
    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)
    //设置运行环境
    val conf = new SparkConf().setAppName("SimpleGraphX").setMaster("local")
    val sc = new SparkContext(conf)
    //设置顶点和边，注意顶点和边都是用元组定义的Array
    //顶点的数据类型是VD:(String,Int)
    val vertexArray = Array(
      (1L, ("Alice", 28)),
      (2L, ("Bob", 27)),
      (3L, ("Charlie", 65)),
      (4L, ("David", 42)),
      (5L, ("Ed", 55)),
      (6L, ("Fran", 50))
    )
    //边的数据类型ED:Int
    val edgeArray = Array(
      Edge(2L, 1L, 7),
      Edge(2L, 4L, 2),
      Edge(3L, 2L, 4),
      Edge(3L, 6L, 3),
      Edge(4L, 1L, 1),
      Edge(5L, 2L, 2),
      Edge(5L, 3L, 8),
      Edge(5L, 6L, 3)
    )
    //构造vertexRDD和edgeRDD
    val vertexRDD: RDD[(Long, (String, Int))] = sc.parallelize(vertexArray)
    val edgeRDD: RDD[Edge[Int]] = sc.parallelize(edgeArray)
    //构造图Graph[VD,ED]
    val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)
    //***********************************************************************************
    //***************************  图的属性    ****************************************
    //**********************************************************************************
    println("***********************************************")
    println("属性演示")
    println("**********************************************************")
    println("找出图中年龄大于30的顶点：")
    graph.vertices.filter { case (id, (name, age)) => age > 30}.collect.foreach {
      case (id, (name, age)) => println(s"$name is $age")
    }
    //边操作：找出图中属性大于5的边
    println("找出图中属性大于5的边：")
graph.edges.filter(e => e.attr > 5).collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))
    println
    //triplets操作，((srcId, srcAttr), (dstId, dstAttr), attr)
    println("列出边属性>5的tripltes：")
    for (triplet <- graph.triplets.filter(t => t.attr > 5).collect) {
      println(s"${triplet.srcAttr._1} likes ${triplet.dstAttr._1}")
    }
    println
    //Degrees操作
    println("找出图中最大的出度、入度、度数：")
    def max(a: (VertexId, Int), b: (VertexId, Int)): (VertexId, Int) = {
      if (a._2 > b._2) a else b
    }
println("max of outDegrees:" + graph.outDegrees.reduce(max) + " max of inDegrees:" + graph.inDegrees.reduce(max) + " max of Degrees:" + graph.degrees.reduce(max))
    println
    //***********************************************************************************
    //***************************  转换操作    ****************************************
    //**********************************************************************************
    println("**********************************************************")
    println("转换操作")
    println("**********************************************************")
    println("顶点的转换操作，顶点age + 10：")
    graph.mapVertices{ case (id, (name, age)) => (id, (name, age+10))}.vertices.collect.foreach(v => println(s"${v._2._1} is ${v._2._2}"))
    println
    println("边的转换操作，边的属性*2：")
    graph.mapEdges(e=>e.attr*2).edges.collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))
    println
      //***********************************************************************************
    //***************************  结构操作    ****************************************
    //**********************************************************************************
    println("**********************************************************")
    println("结构操作")
    println("**********************************************************")
    println("顶点年纪>30的子图：")
    val subGraph = graph.subgraph(vpred = (id, vd) => vd._2 >= 30)
    println("子图所有顶点：")
    subGraph.vertices.collect.foreach(v => println(s"${v._2._1} is ${v._2._2}"))
    println
    println("子图所有边：")
    subGraph.edges.collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))
    println
      //***********************************************************************************
    //***************************  连接操作    ****************************************
    //**********************************************************************************
    println("**********************************************************")
    println("连接操作")
    println("**********************************************************")
    val inDegrees: VertexRDD[Int] = graph.inDegrees
    case class User(name: String, age: Int, inDeg: Int, outDeg: Int)
    //创建一个新图，顶点VD的数据类型为User，并从graph做类型转换
    val initialUserGraph: Graph[User, Int] = graph.mapVertices { case (id, (name, age)) => User(name, age, 0, 0)}
    //initialUserGraph与inDegrees、outDegrees（RDD）进行连接，并修改initialUserGraph中inDeg值、outDeg值
    val userGraph = initialUserGraph.outerJoinVertices(initialUserGraph.inDegrees) {
      case (id, u, inDegOpt) => User(u.name, u.age, inDegOpt.getOrElse(0), u.outDeg)
    }.outerJoinVertices(initialUserGraph.outDegrees) {
      case (id, u, outDegOpt) => User(u.name, u.age, u.inDeg,outDegOpt.getOrElse(0))
    }
    println("连接图的属性：")
userGraph.vertices.collect.foreach(v => println(s"${v._2.name} inDeg: ${v._2.inDeg}  outDeg: ${v._2.outDeg}"))
    println
    println("出度和入读相同的人员：")
    userGraph.vertices.filter {
      case (id, u) => u.inDeg == u.outDeg
    }.collect.foreach {
      case (id, property) => println(property.name)
    }
    println
      //***********************************************************************************
    //***************************  聚合操作    ****************************************
    //**********************************************************************************
    println("**********************************************************")
    println("聚合操作")
    println("**********************************************************")
    println("找出年纪最大的追求者：")
    val oldestFollower: VertexRDD[(String, Int)] = userGraph.mapReduceTriplets[(String, Int)](
      // 将源顶点的属性发送给目标顶点，map过程
      edge => Iterator((edge.dstId, (edge.srcAttr.name, edge.srcAttr.age))),
      // 得到最大追求者，reduce过程
      (a, b) => if (a._2 > b._2) a else b
    )
    userGraph.vertices.leftJoin(oldestFollower) { (id, user, optOldestFollower) =>
      optOldestFollower match {
        case None => s"${user.name} does not have any followers."
        case Some((name, age)) => s"${name} is the oldest follower of ${user.name}."
      }
    }.collect.foreach { case (id, str) => println(str)}
    println
     //***********************************************************************************
    //***************************  实用操作    ****************************************
    //**********************************************************************************
    println("**********************************************************")
    println("聚合操作")
    println("**********************************************************")
    println("找出5到各顶点的最短：")
    val sourceId: VertexId = 5L // 定义源点
    val initialGraph = graph.mapVertices((id, _) => if (id == sourceId) 0.0 else Double.PositiveInfinity)
    val sssp = initialGraph.pregel(Double.PositiveInfinity)(
      (id, dist, newDist) => math.min(dist, newDist),
      triplet => {  // 计算权重
        if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {
          Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))
        } else {
          Iterator.empty
        }
      },
      (a,b) => math.min(a,b) // 最短距离
    )
    println(sssp.vertices.collect.mkString(" "))
    sc.stop()
  }
}
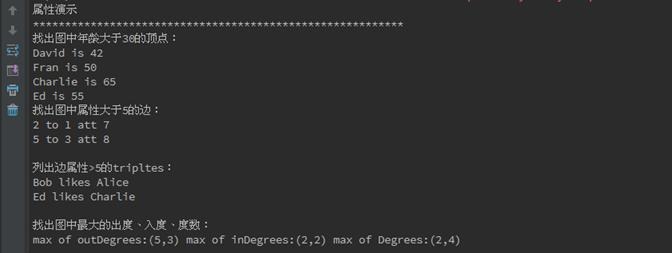
3.1.3 运行结果
在IDEA（如何使用IDEA参见第3课《3.Spark编程模型（下）--IDEA搭建及实战》）中首先对GraphXExample.scala代码进行编译，编译通过后进行执行，执行结果如下：
**********************************************************
属性演示
**********************************************************
找出图中年龄大于30的顶点：
David is 42
Fran is 50
Charlie is 65
Ed is 55
找出图中属性大于5的边：
2 to 1 att 7
5 to 3 att 8
列出边属性>5的tripltes：
Bob likes Alice
Ed likes Charlie
找出图中最大的出度、入度、度数：
max of outDegrees:(5,3) max of inDegrees:(2,2) max of Degrees:(2,4)
**********************************************************
转换操作
**********************************************************
顶点的转换操作，顶点age + 10：
4 is (David,52)
1 is (Alice,38)
6 is (Fran,60)
3 is (Charlie,75)
5 is (Ed,65)
2 is (Bob,37)
边的转换操作，边的属性*2：
2 to 1 att 14
2 to 4 att 4
3 to 2 att 8
3 to 6 att 6
4 to 1 att 2
5 to 2 att 4
5 to 3 att 16
5 to 6 att 6
**********************************************************
结构操作
**********************************************************
顶点年纪>30的子图：
子图所有顶点：
David is 42
Fran is 50
Charlie is 65
Ed is 55

子图所有边：
3 to 6 att 3
5 to 3 att 8
5 to 6 att 3
**********************************************************
连接操作
**********************************************************
连接图的属性：
David inDeg: 1  outDeg: 1
Alice inDeg: 2  outDeg: 0
Fran inDeg: 2  outDeg: 0
Charlie inDeg: 1  outDeg: 2
Ed inDeg: 0  outDeg: 3
Bob inDeg: 2  outDeg: 2
出度和入读相同的人员：
David
Bob
**********************************************************
聚合操作
**********************************************************
找出年纪最大的追求者：
Bob is the oldest follower of David.
David is the oldest follower of Alice.
Charlie is the oldest follower of Fran.
Ed is the oldest follower of Charlie.
Ed does not have any followers.
Charlie is the oldest follower of Bob.
**********************************************************
实用操作
**********************************************************
找出5到各顶点的最短：
(4,4.0)
(1,5.0)
(6,3.0)
(3,8.0)
(5,0.0)
(2,2.0)
3.2 PageRank 演示
 3.2.1 例子介绍
PageRank, 即网页排名，又称网页级别、Google 左侧排名或佩奇排名。它是Google 创始人拉里· 佩奇和谢尔盖· 布林于1997 年构建早期的搜索系统原型时提出的链接分析算法。目前很多重要的链接分析算法都是在PageRank 算法基础上衍生出来的。PageRank 是Google 用于用来标识网页的等级/ 重要性的一种方法，是Google 用来衡量一个网站的好坏的唯一标准。在揉合了诸如Title 标识和Keywords 标识等所有其它因素之后，Google 通过PageRank 来调整结果，使那些更具“等级/ 重要性”的网页在搜索结果中令网站排名获得提升，从而提高搜索结果的相关性和质量。
3.2.2 测试数据
在这里测试数据为顶点数据graphx-wiki-vertices.txt和边数据graphx-wiki-edges.txt，可以在本系列附带资源/data/class9/目录中找到这两个数据文件，其中格式为：
l  顶点为顶点编号和网页标题
l  边数据由两个顶点构成
 3.2.3 程序代码
import org.apache.log4j.{Level, Logger}
import org.apache.spark.{SparkContext, SparkConf}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD

object PageRank {
  def main(args: Array[String]) {
    //屏蔽日志
    Logger.getLogger("org.apache.spark").setLevel(Level.WARN)
    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)
    //设置运行环境
    val conf = new SparkConf().setAppName("PageRank").setMaster("local")
    val sc = new SparkContext(conf)
    //读入数据文件
    val articles: RDD[String] = sc.textFile("/home/hadoop/IdeaProjects/data/graphx/graphx-wiki-vertices.txt")
    val links: RDD[String] = sc.textFile("/home/hadoop/IdeaProjects/data/graphx/graphx-wiki-edges.txt")
    //装载顶点和边
    val vertices = articles.map { line =>
      val fields = line.split(' ')
      (fields(0).toLong, fields(1))
    }
    val edges = links.map { line =>
      val fields = line.split(' ')
      Edge(fields(0).toLong, fields(1).toLong, 0)
    }
    //cache操作
    //val graph = Graph(vertices, edges, "").persist(StorageLevel.MEMORY_ONLY_SER)
    val graph = Graph(vertices, edges, "").persist()
    //graph.unpersistVertices(false)
    //测试
    println("**********************************************************")
    println("获取5个triplet信息")
    println("**********************************************************")
    graph.triplets.take(5).foreach(println(_))
    //pageRank算法里面的时候使用了cache()，故前面persist的时候只能使用MEMORY_ONLY
    println("**********************************************************")
    println("PageRank计算，获取最有价值的数据")
    println("**********************************************************")
    val prGraph = graph.pageRank(0.001).cache()
    val titleAndPrGraph = graph.outerJoinVertices(prGraph.vertices) {
      (v, title, rank) => (rank.getOrElse(0.0), title)
    }
    titleAndPrGraph.vertices.top(10) {
      Ordering.by((entry: (VertexId, (Double, String))) => entry._2._1)
    }.foreach(t => println(t._2._2 + ": " + t._2._1))
    sc.stop()
  }
}
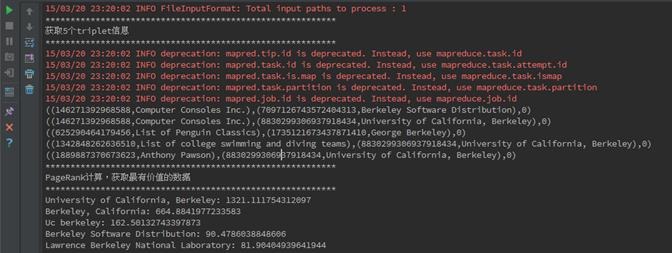
3.2.4 运行结果
在IDEA中首先对PageRank.scala代码进行编译，编译通过后进行执行，执行结果如下：
**********************************************************
获取5个triplet信息
**********************************************************
((146271392968588,Computer Consoles Inc.),(7097126743572404313,Berkeley Software Distribution),0)
((146271392968588,Computer Consoles Inc.),(8830299306937918434,University of California, Berkeley),0)
((625290464179456,List of Penguin Classics),(1735121673437871410,George Berkeley),0)
((1342848262636510,List of college swimming and diving teams),(8830299306937918434,University of California, Berkeley),0)
((1889887370673623,Anthony Pawson),(8830299306937918434,University of California, Berkeley),0)
**********************************************************
PageRank计算，获取最有价值的数据
**********************************************************
University of California, Berkeley: 1321.111754312097
Berkeley, California: 664.8841977233583
Uc berkeley: 162.50132743397873
Berkeley Software Distribution: 90.4786038848606
Lawrence Berkeley National Laboratory: 81.90404939641944
George Berkeley: 81.85226118457985
Busby Berkeley: 47.871998218019655
Berkeley Hills: 44.76406979519754
Xander Berkeley: 30.324075347288037
Berkeley County, South Carolina: 28.908336483710308
4、参考资料
（1）《GraphX:基于Spark的弹性分布式图计算系统》 http://lidrema.blog.163.com/blog/static/20970214820147199643788/
（2）《快刀初试：Spark GraphX在淘宝的实践》 http://www.csdn.net/article/2014-08-07/2821097
概述
- GraphX是 Spark中用于图(如Web-Graphs and Social Networks)和图并行计算(如 PageRank and Collaborative Filtering)的API,可以认为是GraphLab(C++)和Pregel(C++)在Spark(Scala)上的重写及优化，跟其他分布式图计算框架相比，GraphX最大的贡献是，在Spark之上提供一站式数据解决方案，可以方便且高效地完成图计算的一整套流水作业。
- Graphx是Spark生态中的非常重要的组件，融合了图并行以及数据并行的优势，虽然在单纯的计算机段的性能相比不如GraphLab等计算框架，但是如果从整个图处理流水线的视角（图构建，图合并，最终结果的查询）看，那么性能就非常具有竞争性了。
图计算应用场景
    “图计算”是以“图论”为基础的对现实世界的一种“图”结构的抽象表达，以及在这种数据结构上的计算模式。通常，在图计算中，基本的数据结构表达就是：G = （V，E，D） V = vertex （顶点或者节点） E = edge （边） D = data （权重）。
    图数据结构很好的表达了数据之间的关联性，因此，很多应用中出现的问题都可以抽象成图来表示，以图论的思想或者以图为基础建立模型来解决问题。
下面是一些图计算的应用场景：
PageRank让链接来”投票”
基于GraphX的社区发现算法FastUnfolding分布式实现
http://bbs.pinggu.org/thread-3614747-1-1.html
社交网络分析
如基于Louvian社区发现的新浪微博社交网络分析
社交网络最适合用图来表达和计算了，图的“顶点”表示社交中的人，“边”表示人与人之间的关系。
基于三角形计数的关系衡量
基于随机游走的用户属性传播
推荐应用
如淘宝推荐商品，腾讯推荐好友等等（同样是基于社交网络这个大数据，可以很好构建一张大图）
淘宝应用
度分布、二跳邻居数、连通图、多图合并、能量传播模型
所有的关系都可以从“图”的角度来看待和处理，但到底一个关系的价值多大？健康与否？适合用于什么场景？
快刀初试：Spark GraphX在淘宝的实践
http://www.csdn.net/article/2014-08-07/2821097
Spark中图的建立及图的基本操作
图的构建
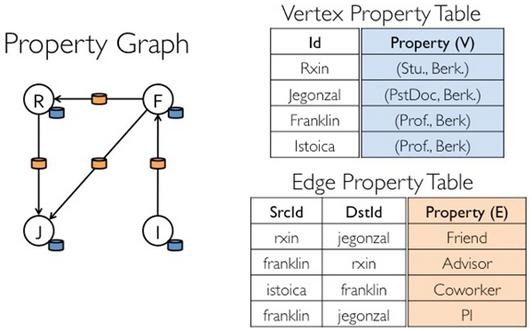
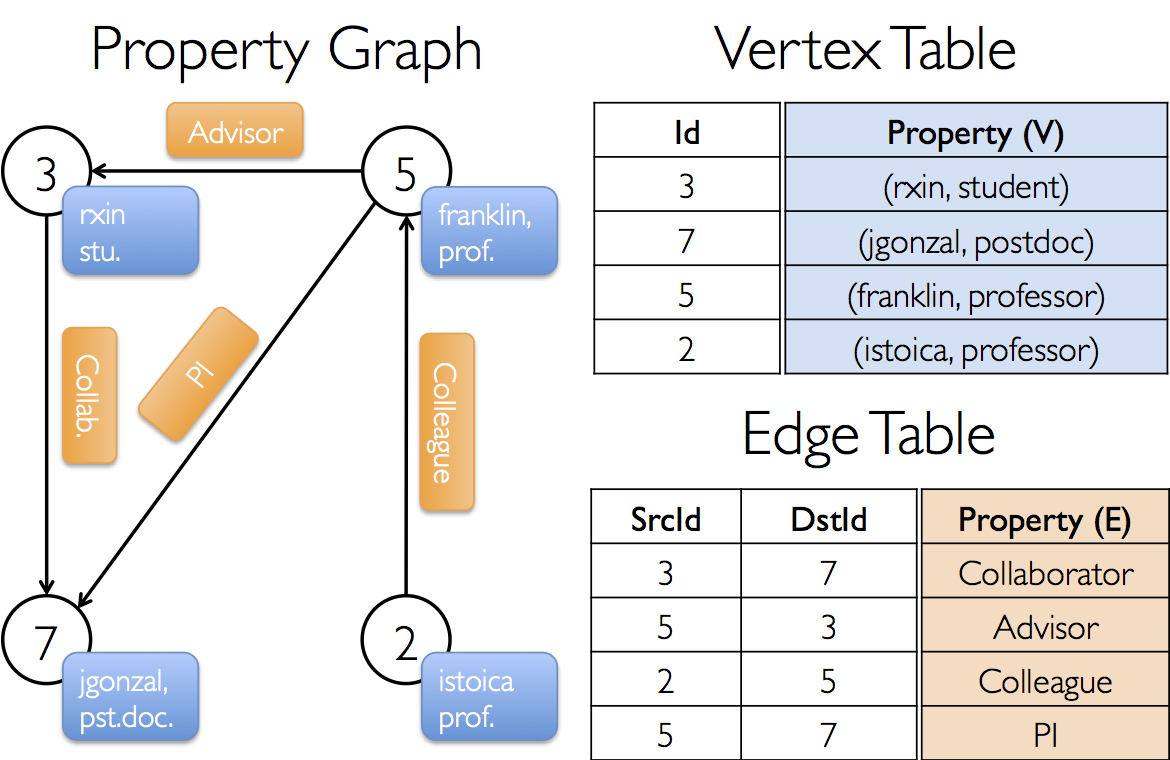
          首先利用“顶点”和“边”RDD建立一个简单的属性图，通过这个例子，了解完整的GraphX图构建的基本流程。
          如下图所示，顶点的属性包含用户的姓名和职业，带标注的边表示不同用户之间的关系。
```
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext

import org.apache.spark._
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD

object myGraphX {

  def main(args:Array[String]){

    // Create the context  
    val sparkConf = new SparkConf().setAppName("myGraphPractice").setMaster("local[2]")
    val sc=new SparkContext(sparkConf) 

    // 顶点RDD[顶点的id,顶点的属性值]
    val users: RDD[(VertexId, (String, String))] =
      sc.parallelize(Array((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")),
                       (5L, ("franklin", "prof")), (2L, ("istoica", "prof"))))
    // 边RDD[起始点id,终点id，边的属性（边的标注,边的权重等）]
    val relationships: RDD[Edge[String]] =
      sc.parallelize(Array(Edge(3L, 7L, "collab"),    Edge(5L, 3L, "advisor"),
                       Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi")))
    // 默认（缺失）用户
    //Define a default user in case there are relationship with missing user
    val defaultUser = ("John Doe", "Missing")

    //使用RDDs建立一个Graph（有许多建立Graph的数据来源和方法，后面会详细介绍）
    val graph = Graph(users, relationships, defaultUser)     
  }
}
```
上面是一个简单的例子，说明如何建立一个属性图，那么建立一个图主要有哪些方法呢？我们先看图的定义：
```
object Graph {
  def apply[VD, ED](
      vertices: RDD[(VertexId, VD)],
      edges: RDD[Edge[ED]],
      defaultVertexAttr: VD = null)
    : Graph[VD, ED]

  def fromEdges[VD, ED](
      edges: RDD[Edge[ED]],
      defaultValue: VD): Graph[VD, ED]

  def fromEdgeTuples[VD](
      rawEdges: RDD[(VertexId, VertexId)],
      defaultValue: VD,
      uniqueEdges: Option[PartitionStrategy] = None): Graph[VD, Int]

}
```
- 由上面的定义我们可以看到，GraphX主要有三种方法可以建立图：
（1）在构造图的时候，会自动使用apply方法，因此前面那个例子中实际上就是使用apply方法。相当于Java/C++语言的构造函数。有三个参数，分别是：vertices: RDD[(VertexId, VD)], edges: RDD[Edge[ED]], defaultVertexAttr: VD = null)，前两个必须有，最后一个可选择。“顶点“和”边“的RDD来自不同的数据源，与Spark中其他RDD的建立并没有区别。
这里再举读取文件，产生RDD，然后利用RDD建立图的例子：
（1）读取文件，建立顶点和边的RRD，然后利用RDD建立属性图
```
//读入数据文件
val articles: RDD[String] = sc.textFile("E:/data/graphx/graphx-wiki-vertices.txt")
val links: RDD[String] = sc.textFile("E:/data/graphx/graphx-wiki-edges.txt")

//装载“顶点”和“边”RDD
val vertices = articles.map { line =>
    val fields = line.split('	')
      (fields(0).toLong, fields(1))
    }//注意第一列为vertexId，必须为Long，第二列为顶点属性，可以为任意类型，包括Map等序列。

val edges = links.map { line =>
    val fields = line.split('	')
      Edge(fields(0).toLong, fields(1).toLong, 1L)//起始点ID必须为Long，最后一个是属性，可以为任意类型
    }
//建立图
val graph = Graph(vertices, edges, "").persist()//自动使用apply方法建立图
```
（2）Graph.fromEdges方法:这种方法相对而言最为简单，只是由”边”RDD建立图，由边RDD中出现所有“顶点”（无论是起始点src还是终点dst）自动产生顶点vertextId，顶点的属性将被设置为一个默认值。
Graph.fromEdges allows creating a graph from only an RDD of edges, automatically creating any vertices mentioned by edges and assigning them the default value.
举例如下：
```
//读入数据文件        
val records: RDD[String] = sc.textFile("/microblogPCU/microblogPCU/follower_followee")   
//微博数据：000000261066,郜振博585,3044070630,redashuaicheng,1929305865,1994,229,3472,male,first
// 第三列是粉丝Id：3044070630,第五列是用户Id：1929305865
val followers=records.map {case x => val fields=x.split(",")
          Edge(fields(2).toLong, fields(4).toLong,1L )       
      }    
val graph=Graph.fromEdges(followers, 1L)
```
（3）Graph.fromEdgeTuples方法
          Graph.fromEdgeTuples allows creating a graph from only an RDD of edge tuples, assigning the edges the value 1, and automatically creating any vertices mentioned by edges and assigning them the default value. It also supports deduplicating the edges; to deduplicate, pass Some of a PartitionStrategy as the uniqueEdges parameter (for example, uniqueEdges = Some(PartitionStrategy.RandomVertexCut)). A partition strategy is necessary to colocate identical edges on the same partition so they can be deduplicated.
          除了三种方法，还可以用GraphLoader构建图。如下面GraphLoader.edgeListFile：
（4）GraphLoader.edgeListFile建立图的基本结构,然后Join属性
(a)首先建立图的基本结构：
          利用GraphLoader.edgeListFile函数从边List文件中建立图的基本结构（所有“顶点”+“边”），且顶点和边的属性都默认为1。
```
object GraphLoader {
  def edgeListFile(
      sc: SparkContext,
      path: String,
      canonicalOrientation: Boolean = false,
      minEdgePartitions: Int = 1)
    : Graph[Int, Int]
}
```
使用方法如下：
```
val graph=GraphLoader.edgeListFile(sc, "/data/graphx/followers.txt") 
//文件的格式如下：
//2 1
//4 1
//1 2  依次为第一个顶点和第二个顶点
```
（b)然后读取属性文件，获得RDD后和（1）中得到的基本结构图join在一起，就可以组合成完整的属性图。
三种视图及操作
Spark中图有以下三种视图可以访问，分别通过graph.vertices，graph.edges，graph.triplets来访问。
在Scala语言中，可以用case语句进行形式简单、功能强大的模式匹配
```
//假设graph顶点属性(String,Int)-(name,age),边有一个权重（int)
val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)
用case匹配可以很方便访问顶点和边的属性及id
graph.vertices.map{
      case (id,(name,age))=>//利用case进行匹配
        (age,name)//可以在这里加上自己想要的任何转换
    }

graph.edges.map{
      case Edge(srcid,dstid,weight)=>//利用case进行匹配
        (dstid,weight*0.01)//可以在这里加上自己想要的任何转换
    }
```
也可以通过下标访问
```
graph.vertices.map{
      v=>(v._1,v._2._1,v._2._2)//v._1,v._2._1,v._2._2分别对应Id，name，age
}

graph.edges.map {
      e=>(e.attr,e.srcId,e.dstId)
}

graph.triplets.map{
      triplet=>(triplet.srcAttr._1,triplet.dstAttr._2,triplet.srcId,triplet.dstId)
    }
```
可以不用graph.vertices先提取顶点再map的方法，也可以通过graph.mapVertices直接对顶点进行map，返回是相同结构的另一个Graph，访问属性的方法和上述方法是一模一样的。如下：
```
graph.mapVertices{
      case (id,(name,age))=>//利用case进行匹配
        (age,name)//可以在这里加上自己想要的任何转换
}

graph.mapEdges(e=>(e.attr,e.srcId,e.dstId))

graph.mapTriplets(triplet=>(triplet.srcAttr._1))
```
Spark GraphX中的图的函数大全
```
/** Summary of the functionality in the property graph */
class Graph[VD, ED] {
  // Information about the Graph 
  //图的基本信息统计
===================================================================
  val numEdges: Long
  val numVertices: Long
  val inDegrees: VertexRDD[Int]
  val outDegrees: VertexRDD[Int]
  val degrees: VertexRDD[Int]

  // Views of the graph as collections 
  // 图的三种视图
=============================================================
  val vertices: VertexRDD[VD]
  val edges: EdgeRDD[ED]
  val triplets: RDD[EdgeTriplet[VD, ED]]

  // Functions for caching graphs ==================================================================
  def persist(newLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]
  def cache(): Graph[VD, ED]
  def unpersistVertices(blocking: Boolean = true): Graph[VD, ED]
  // Change the partitioning heuristic  ============================================================
  def partitionBy(partitionStrategy: PartitionStrategy): Graph[VD, ED]

  // Transform vertex and edge attributes 
  // 基本的转换操作
==========================================================
  def mapVertices[VD2](map: (VertexID, VD) => VD2): Graph[VD2, ED]
  def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
  def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]
  def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
  def mapTriplets[ED2](map: (PartitionID, Iterator[EdgeTriplet[VD, ED]]) => Iterator[ED2])
    : Graph[VD, ED2]

  // Modify the graph structure 
  //图的结构操作（仅给出四种基本的操作，子图提取是比较重要的操作）
====================================================================
  def reverse: Graph[VD, ED]
  def subgraph(
      epred: EdgeTriplet[VD,ED] => Boolean = (x => true),
      vpred: (VertexID, VD) => Boolean = ((v, d) => true))
    : Graph[VD, ED]
  def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]
  def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED]

  // Join RDDs with the graph 
  // 两种聚合方式，可以完成各种图的聚合操作  ======================================================================
  def joinVertices[U](table: RDD[(VertexID, U)])(mapFunc: (VertexID, VD, U) => VD): Graph[VD, ED]
  def outerJoinVertices[U, VD2](other: RDD[(VertexID, U)])
      (mapFunc: (VertexID, VD, Option[U]) => VD2)

  // Aggregate information about adjacent triplets 
  //图的邻边信息聚合，collectNeighborIds都是效率不高的操作，优先使用aggregateMessages，这也是GraphX最重要的操作之一。
  =================================================
  def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexID]]
  def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexID, VD)]]
  def aggregateMessages[Msg: ClassTag](
      sendMsg: EdgeContext[VD, ED, Msg] => Unit,
      mergeMsg: (Msg, Msg) => Msg,
      tripletFields: TripletFields = TripletFields.All)
    : VertexRDD[A]

  // Iterative graph-parallel computation ==========================================================
  def pregel[A](initialMsg: A, maxIterations: Int, activeDirection: EdgeDirection)(
      vprog: (VertexID, VD, A) => VD,
      sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexID,A)],
      mergeMsg: (A, A) => A)
    : Graph[VD, ED]

  // Basic graph algorithms 
  //图的算法API（目前给出了三类四个API）  ========================================================================
  def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double]
  def connectedComponents(): Graph[VertexID, ED]
  def triangleCount(): Graph[Int, ED]
  def stronglyConnectedComponents(numIter: Int): Graph[VertexID, ED]
}
```
结构操作
Structural Operators
Spark2.0版本中，仅仅有四种最基本的结构操作，未来将开发更多的结构操作。
```
class Graph[VD, ED] {
  def reverse: Graph[VD, ED]
  def subgraph(epred: EdgeTriplet[VD,ED] => Boolean,
               vpred: (VertexId, VD) => Boolean): Graph[VD, ED]
  def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]
  def groupEdges(merge: (ED, ED) => ED): Graph[VD,ED]
}
```
子图subgraph
      子图(subgraph)是图论的基本概念之一。子图是指节点集和边集分别是某一图的节点集的子集和边集的子集的图。
  Spark API–subgraph利用EdgeTriplet（epred）或/和顶点（vpred）满足一定条件，来提取子图。利用这个操作可以使顶点和边被限制在感兴趣的范围内，比如删除失效的链接。
        The subgraph operator takes vertex and edge predicates and returns the graph containing only the vertices that satisfy the vertex predicate (evaluate to true) and edges that satisfy the edge predicate and connect vertices that satisfy the vertex predicate. The subgraph operator can be used in number of situations to restrict the graph to the vertices and edges of interest or eliminate broken links. For example in the following code we remove broken links:
```
//假设graph有如下的顶点和边 顶点RDD(id,(name,age) 边上有一个Int权重（属性）
(4,(David,42))(6,(Fran,50))(2,(Bob,27)) (1,(Alice,28))(3,(Charlie,65))(5,(Ed,55))
Edge(5,3,8)Edge(2,1,7)Edge(3,2,4) Edge(5,6,3)Edge(3,6,3)

//可以使用以下三种操作方法获取满足条件的子图
//方法1，对顶点进行操作
val subGraph1=graph.subgraph(vpred=(id,attr)=>attr._2>30)
//vpred=(id,attr)=>attr._2>30 顶点vpred第二个属性（age）>30岁
subGraph1.vertices.foreach(print)
println
subGraph1.edges.foreach {print}
println
输出结果：
顶点：(4,(David,42))(6,(Fran,50))(3,(Charlie,65))(5,(Ed,55))
边：Edge(3,6,3)Edge(5,3,8)Edge(5,6,3)

//方法2--对EdgeTriplet进行操作
val subGraph2=graph.subgraph(epred=>epred.attr>2)
//epred（边）的属性（权重）大于2
输出结果：
顶点：(4,(David,42))(6,(Fran,50))(2,(Bob,27))(1,(Alice,28)) (3,(Charlie,65))(5,(Ed,55))
边：Edge(5,3,8)Edge(5,6,3)Edge(2,1,7)Edge(3,2,4) Edge(3,6,3)
//也可以定义如下的操作
val subGraph2=graph.subgraph(epred=>pred.srcAttr._2<epred.dstAttr._2))
//起始顶点的年龄小于终点顶点年龄
顶点：1,(Alice,28))(4,(David,42))(3,(Charlie,65))(6,(Fran,50)) (2,(Bob,27))(5,(Ed,55))
边 ：Edge(5,3,8)Edge(2,1,7)Edge(2,4,2)

//方法3--对顶点和边Triplet两种同时操作“，”号隔开epred和vpred
val subGraph3=graph.subgraph(epred=>epred.attr>3,vpred=(id,attr)=>attr._2>30)
输出结果：
顶点：(3,(Charlie,65))(5,(Ed,55))(4,(David,42))(6,(Fran,50))
边：Edge(5,3,8)
```
图的基本信息统计-度计算
度分布：这是一个图最基础和重要的指标。度分布检测的目的，主要是了解图中“超级节点”的个数和规模，以及所有节点度的分布曲线。超级节点的存在对各种传播算法都会有重大的影响（不论是正面助力还是反面阻力），因此要预先对这些数据量有个预估。借助GraphX最基本的图信息接口degrees: VertexRDD[Int]（包括inDegrees和outDegrees），这个指标可以轻松计算出来，并进行各种各样的统计（摘自《快刀初试：Spark GraphX在淘宝的实践》。
```
//-----------------度的Reduce，统计度的最大值-----------------
def max(a:(VertexId,Int),b:(VertexId,Int)):(VertexId,Int)={
            if (a._2>b._2) a  else b }

val totalDegree=graph.degrees.reduce((a,b)=>max(a, b))
val inDegree=graph.inDegrees.reduce((a,b)=>max(a,b))
val outDegree=graph.outDegrees.reduce((a,b)=>max(a,b))

print("max total Degree = "+totalDegree)
print("max in Degree = "+inDegree)
print("max out Degree = "+outDegree)
//小技巧：如何知道a和b的类型为(VertexId,Int)？
//当你敲完graph.degrees.reduce((a,b)=>，再将鼠标点到a和b上查看，
//就会发现a和b是(VertexId,Int)，当然reduce后的返回值也是(VertexId,Int)
//这样就很清楚自己该如何定义max函数了  

//平均度
val sumOfDegree=graph.degrees.map(x=>(x._2.toLong)).reduce((a,b)=>a+b)    
val meanDegree=sumOfDegree.toDouble/graph.vertices.count().toDouble
print("meanDegree "+meanDegree)
println     

//------------------使用RDD自带的统计函数进行度分布分析--------
//度的统计分析
//最大，最小
val degree2=graph.degrees.map(a=>(a._2,a._1))
//graph.degrees是VertexRDD[Int],即（VertexID，Int）。
//通过上面map调换成map(a=>(a._2,a._1)),即RDD[(Int,VetexId)]
//这样下面就可以将度（Int）当作键值（key）来操作了，
//包括下面的min，max，sortByKey，top等等，因为这些函数都是对第一个值也就是key操作的
//max degree
print("max degree = " + (degree2.max()._2,degree2.max()._1))
println

//min degree
print("min degree =" +(degree2.min()._2,degree2.min()._1))
println

//top（N） degree"超级节点"
print("top 3 degrees:
")   
degree2.sortByKey(true, 1).top(3).foreach(x=>print(x._2,x._1))
println

/*输出结果：
 * max degree = (2,4)//（Vetext，degree）
 * min degree =（1,2)
 * top 3 degrees:
 * (2,4)(5,3)(3,3)
 */ 
```
相邻聚合—消息聚合
       相邻聚合（Neighborhood Aggregation）
       图分析任务的一个关键步骤是汇总每个顶点附近的信息。例如我们可能想知道每个用户的追随者的数量或者每个用户的追随者的平均年龄。许多迭代图算法（如PageRank，最短路径和连通体）多次聚合相邻顶点的属性。
       聚合消息(aggregateMessages)
GraphX中的核心聚合操作是 aggregateMessages，它主要功能是向邻边发消息，合并邻边收到的消息，返回messageRDD。这个操作将用户定义的sendMsg函数应用到图的每个边三元组(edge triplet)，然后应用mergeMsg函数在其目的顶点聚合这些消息。
```
class Graph[VD, ED] {
  def aggregateMessages[Msg: ClassTag](
      sendMsg: EdgeContext[VD, ED, Msg] => Unit,//(1)--sendMsg:向邻边发消息,相当与MR中的Map函数
      mergeMsg: (Msg, Msg) => Msg,//(2)--mergeMsg:合并邻边收到的消息，相当于Reduce函数
      tripletFields: TripletFields = TripletFields.All)//(3)可选项，TripletFields.Src/Dst/All
    : VertexRDD[Msg]//(4)--返回messageRDD
}
```
（1）sendMsg：
将sendMsg函数看做map-reduce过程中的map函数，向邻边发消息，应用到图的每个边三元组(edge triplet)，即函数的左侧为每个边三元组(edge triplet)。
The user defined sendMsg function takes an EdgeContext, which exposes the source and destination attributes along with the edge attribute and functions (sendToSrc, and sendToDst) to send messages to the source and destination attributes. Think of sendMsg as the map function in map-reduce.
```
//关键数据结构EdgeContext源码解析

package org.apache.spark.graphx

/**
 * Represents an edge along with its neighboring vertices and allows sending messages along the
 * edge. Used in [[Graph#aggregateMessages]].
 */
abstract class EdgeContext[VD, ED, A] {//三个类型分别是：顶点、边、自定义发送消息的类型（返回值的类型）
  /** The vertex id of the edge's source vertex. */
  def srcId: VertexId
  /** The vertex id of the edge's destination vertex. */
  def dstId: VertexId
  /** The vertex attribute of the edge's source vertex. */
  def srcAttr: VD
  /** The vertex attribute of the edge's destination vertex. */
  def dstAttr: VD
  /** The attribute associated with the edge. */
  def attr: ED

  /** Sends a message to the source vertex. */
  def sendToSrc(msg: A): Unit
  /** Sends a message to the destination vertex. */
  def sendToDst(msg: A): Unit

  /** Converts the edge and vertex properties into an [[EdgeTriplet]] for convenience. */
  def toEdgeTriplet: EdgeTriplet[VD, ED] = {
    val et = new EdgeTriplet[VD, ED]
    et.srcId = srcId
    et.srcAttr = srcAttr
    et.dstId = dstId
    et.dstAttr = dstAttr
    et.attr = attr
    et
  }
}
```
（2）mergeMsg ：
用户自定义的mergeMsg函数指定两个消息到相同的顶点并保存为一个消息。可以将mergeMsg函数看做map-reduce过程中的reduce函数。
The user defined mergeMsg function takes two messages destined to the same vertex and yields a single message. Think of mergeMsg as the reduce function in map-reduce.
```
这里写代码片
```
（3）TripletFields可选项
        它指出哪些数据将被访问（源顶点特征，目的顶点特征或者两者同时，即有三种可选择的值：TripletFields.Src，TripletFieldsDst，TripletFields.All。
      因此这个参数的作用是通知GraphX仅仅只需要EdgeContext的一部分参与计算，是一个优化的连接策略。例如，如果我们想计算每个用户的追随者的平均年龄，我们仅仅只需要源字段。所以我们用TripletFields.Src表示我们仅仅只需要源字段。
     takes an optional tripletsFields which indicates what data is accessed in the EdgeContext (i.e., the source vertex attribute but not the destination vertex attribute). The possible options for the tripletsFields are defined in TripletFields and the default value is TripletFields.All which indicates that the user defined sendMsg function may access any of the fields in the EdgeContext. The tripletFields argument can be used to notify GraphX that only part of the EdgeContext will be needed allowing GraphX to select an optimized join strategy. For example if we are computing the average age of the followers of each user we would only require the source field and so we would use TripletFields.Src to indicate that we only require the source field
（4）返回值：
    The aggregateMessages operator returns a VertexRDD[Msg] containing the aggregate message (of type Msg) destined to each vertex. Vertices that did not receive a message are not included in the returned VertexRDD.
```
//假设已经定义好如下图：
//顶点:[Id,(name,age)]
//(4,(David,18))(1,(Alice,28))(6,(Fran,40))(3,(Charlie,30))(2,(Bob,70))(5,Ed,55))
//边：Edge(4,2,2)Edge(2,1,7)Edge(4,5,8)Edge(2,4,2)Edge(5,6,3)Edge(3,2,4)
//    Edge(6,1,2)Edge(3,6,3)Edge(6,2,8)Edge(4,1,1)Edge(6,4,3)(4,(2,110))

//定义一个相邻聚合，统计比自己年纪大的粉丝数（count）及其平均年龄（totalAge/count)
val olderFollowers=graph.aggregateMessages[(Int,Int)](
//方括号内的元组(Int,Int)是函数返回值的类型，也就是Reduce函数（mergeMsg )右侧得到的值（count，totalAge）
        triplet=> {
          if(triplet.srcAttr._2>triplet.dstAttr._2){            
              triplet.sendToDst((1,triplet.srcAttr._2))
          }
        },//(1)--函数左侧是边三元组，也就是对边三元组进行操作，有两种发送方式sendToSrc和 sendToDst
        (a,b)=>(a._1+b._1,a._2+b._2),//(2)相当于Reduce函数，a，b各代表一个元组（count，Age）
        //对count和Age不断相加（reduce），最终得到总的count和totalAge
        TripletFields.All)//(3)可选项,TripletFields.All/Src/Dst
olderFollowers.collect().foreach(println)
输出结果：
(4,(2,110))//顶点Id=4的用户，有2个年龄比自己大的粉丝，同年龄是110岁
(6,(1,55))
(1,(2,110))

//计算平均年龄
val averageOfOlderFollowers=olderFollowers.mapValues((id,value)=>value match{
      case (count,totalAge) =>(count,totalAge/count)//由于不是所有顶点都有结果，所以用match-case语句
    })    

averageOfOlderFollowers.foreach(print)  
输出结果：
(1,(2,55))(4,(2,55))(6,(1,55))//Id=1的用户，有2个粉丝，平均年龄是55岁
```
Spark Join连接操作
许多情况下，需要将图与外部获取的RDDs进行连接。比如将一个额外的属性添加到一个已经存在的图上，或者将顶点属性从一个图导出到另一图中(在自己编写图计算API 时，往往需要多次进行aggregateMessages和Join操作，因此这两个操作可以说是Graphx中非常重要的操作，需要非常熟练地掌握，在本文最后的实例中，有更多的例子可供学习）
In many cases it is necessary to join data from external collections (RDDs) with graphs. For example, we might have extra user properties that we want to merge with an existing graph or we might want to pull vertex properties from one graph into another.
有两个join API可供使用：
```
class Graph[VD, ED] {
  def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD)
    : Graph[VD, ED]

  def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2)
    : Graph[VD2, ED]
}
```
         两个连接方式差别非常大。下面分别来说明
joinVertices连接
          返回值的类型就是graph顶点属性的类型，不能新增，也不可以减少（即不能改变原始graph顶点属性类型和个数）。
         经常会遇到这样的情形，”一个额外的费用（extraCost）增加到老的费用（oldCost）中”，oldCost为graph的顶点属性值，extraCost来自外部RDD，这时候就要用到joinVertices：
         extraCosts: RDD[(VertexID, Double)]//额外的费用
         graph:Graph[Double,Long]//oldCost
         val totlCosts = graph.joinVertices(extraCosts)( (id, oldCost, extraCost) => oldCost + extraCost)
         //extraCost和oldCost数据类型一致，且返回时无需改变原始graph顶点属性的类型。
再举一个例子：
```
// 假设graph的顶点如下[id,(user_name,initial_energy)]
//(6,(Fran,0))(2,(Bob,3))(4,(David,3))(3,(Charlie,1))(1,(Alice,2))(5,(Ed,2))

// graph边如下：
//Edge(2,1,1)Edge(2,4,1)Edge(4,1,1)Edge(5,2,1)Edge(5,3,1)Edge(5,6,1)Edge(3,2,1)Edge(3,6,1)

// 每个src向dst邻居发送生命值为2能量
val energys=graph.aggregateMessages[Long](
            triplet=>triplet.sendToDst(2), (a,b)=>a+b)      

// 输出结果：
// (1,4)(4,2)(3,2)(6,4)(2,4)
val energys_name=graph.joinVertices(energys){
              case(id,(name,initialEnergy),energy)=>(name,initialEnergy+energy)
              }
//输出结果：
// (3,(Charlie,3))(1,(Alice,6))(5,(Ed,2))(4,(David,5))(6,(Fran,4))(2,(Bob,7))

// 我们注意到，如果energys：RDD中没有graph某些顶点对应的值，则graph不进行任何改变，如(5,(Ed,2))。
```
从上面的例子我们知道：将外部RDD joinvertices到graph中，对应于graph某些顶点，RDD中无对应的属性，则保留graph原有属性值不进行任何改变。
而与之相反的是另一种情况，对应于graph某一些顶点，RDD中的值不止一个，这种情况下将只有一个值在join时起作用。可以先使用aggregateUsingIndex的进行reduce操作，然后再join graph。
```
val nonUniqueCosts: RDD[(VertexID, Double)]
val uniqueCosts: VertexRDD[Double] =
  graph.vertices.aggregateUsingIndex(nonUnique, (a,b) => a + b)
val joinedGraph = graph.joinVertices(uniqueCosts)(
  (id, oldCost, extraCost) => oldCost + extraCost)
```
         If the RDD contains more than one value for a given vertex only one will be used. It is therefore recommended that the input RDD be made unique using the following which will also pre-index the resulting values to substantially accelerate the subsequent join.
（2）outerJoinVertices
         更为常用，使用起来也更加自由的是outerJoinVertices，至于为什么后面会详细分析。
         The more general outerJoinVertices behaves similarly to joinVertices except that the user defined map function is applied to all vertices and can change the vertex property type. Because not all vertices may have a matching value in the input RDD the map function takes an Option type.
         从下面函数的定义我们注意到，与前面JoinVertices不同之处在于map函数右侧类型是VD2，不再是VD，因此不受原图graph顶点属性类型VD的限制，在outerJoinVertices中使用者可以随意定义自己想要的返回类型，从而可以完全改变图的顶点属性值的类型和属性的个数。
```
class Graph[VD, ED] {

  def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2)
    : Graph[VD2, ED]

}
```
用上面例子中的graph和energys数据：
```
 val graph_energy_total=graph.outerJoinVertices(energys){
      case(id,(name,initialEnergy),Some(energy))=>(name,initialEnergy,energy,initialEnergy+energy)
      case(id,(name,initialEnergy),None)=>(name,initialEnergy,0,initialEnergy)
    }

// 输出结果:
// (3,(Charlie,1,2,3))(1,(Alice,2,4,6))(5,(Ed,2,0,2))
// (4,(David,3,2,5))(6,(Fran,0,4,4))(2,(Bob,3,4,7))
```
Spark Scala几个语法问题
（1）遇到null怎么处理？
可参考【Scala】使用Option、Some、None，避免使用null
http://www.jianshu.com/p/95896d06a94d
         大多数语言都有一个特殊的关键字或者对象来表示一个对象引用的是“无”，在Java，它是null。
         Scala鼓励你在变量和函数返回值可能不会引用任何值的时候使用Option类型。在没有值的时候，使用None，这是Option的一个子类。如果有值可以引用，就使用Some来包含这个值。Some也是Option的子类。
         通过模式匹配分离可选值，如果匹配的值是Some的话，将Some里的值抽出赋给x变量。举一个综合的例子：
```
def showCapital(x: Option[String]) = x match {
    case Some(s) => s
    case None => "?"
}

/*
Option用法：Scala推荐使用Option类型来代表一些可选值。使用Option类型，读者一眼就可以看出这种类型的值可能为None。
如上面：x: Option[String])参数，就是因为参数可能是String，也可能为null，这样程序不会在为null时抛出异常
*/
```
Spark中，经常使用在map中使用case语句进行匹配None和Some，再举一个例子
```
//假设graph.Vertice:(id，（name，weight））如下：
//(4,(David,Some(2)))(3,(Charlie,Some(2)))(6,(Fran,Some(4)))(2,(Bob,Some(4)))(1,(Alice,Some(4)))(5,(Ed,None))
//id=5时，weight=None，其他的为Some

val weights=graph.vertices.map{
      case (id,(name,Some(weight)))=>(id,weight)
      case (id,(name,None))=>(id,0)
    }    
weights.foreach(print)
println

//输出结果如下(id,weight)：
//(3,2)(6,4)(2,4)(4,2)(1,4)(5,0)
```
在上面的例子中，其实我们也可以选用另外一个方法，getOrElse。这个方法在这个Option是Some的实例时返回对应的值，而在是None的实例时返函数参数。
上面例子可以用下面的语句获得同样的结果：
```
val weights=graph.vertices.map{
      attr=>(attr._1,attr._2._2.getOrElse(0))
      //如果attr._2._2！=None，返回attr._2._2（weight）的值，
      //否则（即attr._2._2==None），返回自己设置的函数参数（0）
    }

//输出同样的结果：
//(id,weight)
(4,2)(6,4)(2,4)(3,2)(1,4)(5,0)
```
图算法工具包
1.数三角形
TriangleCount主要用途之一是用于社区发现，如下图所示：

例如说在微博上你关注的人也互相关注，大家的关注关系中就会有很多三角形，这说明社区很强很稳定，大家的联系都比较紧密；如果说只是你一个人关注很多人，这说明你的社交群体是非常小的。(摘自《大数据Spark企业级实战》一书）
```
graph.triangleCount().vertices.foreach(x=>print(x+"
"))
    /*输出结果
     * (1,1)//顶点1有1个三角形
     * (3,2)//顶点3有2个三角形
     * (5,2)
     * (4,1)
     * (6,1)
     * (2,2)
     */
```
2.连通图
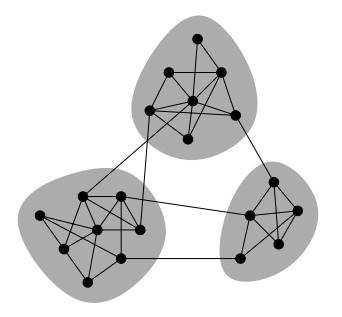
        现实生活中存在各种各样的网络，诸如人际关系网、交易网、运输网等等。对这些网络进行社区发现具有极大的意义，如在人际关系网中，可以发现出具有不同兴趣、背景的社会团体，方便进行不同的宣传策略；在交易网中，不同的社区代表不同购买力的客户群体，方便运营为他们推荐合适的商品；在资金网络中，社区有可能是潜在的洗钱团伙、刷钻联盟，方便安全部门进行相应处理；在相似店铺网络中，社区发现可以检测出商帮、价格联盟等，对商家进行指导等等。总的来看，社区发现在各种具体的网络中都能有重点的应用场景，图1展示了基于图的拓扑结构进行社区发现的例子。
        检测连通图可以弄清一个图有几个连通部分及每个连通部分有多少顶点。这样可以将一个大图分割为多个小图，并去掉零碎的连通部分，从而可以在多个小子图上进行更加精细的操作。目前，GraphX提供了ConnectedComponents和StronglyConnected-Components算法，使用它们可以快速计算出相应的连通图。
        连通图可以进一步演化变成社区发现算法，而该算法优劣的评判标准之一，是计算模块的Q值，来查看所谓的modularity情况。
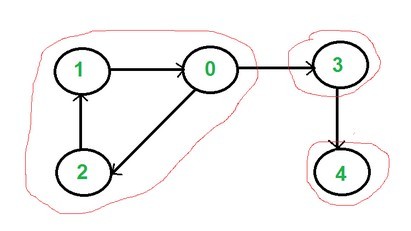
         如果一个有向图中的每对顶点都可以从通过路径可达，那么就称这个图是强连通的。一个 strongly connected component就是一个有向图中最大的强连通子图。下图中就有三个强连通子图：
```
//连通图
def connectedComponents(maxIterations: Int): Graph[VertexId, ED]
def connectedComponents(): Graph[VertexId, ED]

//强连通图
//numIter：the maximum number of iterations to run for
def stronglyConnectedComponents(numIter: Int): Graph[VertexId, ED]
```
```
//连通图计算社区发现
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.log4j.{Level, Logger}

import org.apache.spark._
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD

object myConnectComponent {
  def main(args:Array[String]){    

    val sparkConf = new SparkConf().setAppName("myGraphPractice").setMaster("local[2]")
    val sc=new SparkContext(sparkConf) 
    //屏蔽日志
    Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)

    val graph=GraphLoader.edgeListFile(sc, "/spark-2.0.0-bin-hadoop2.6/data/graphx/followers.txt")    

    graph.vertices.foreach(print)
    println
    graph.edges.foreach(print)  
    println

    val cc=graph.connectedComponents().vertices
    cc.foreach(print)
    println 
    /*输出结果 
     *  (VertexId,cc)
     * (4,1)(1,1)(6,1)(3,1)(2,1)(7,1)
     */

    //强连通图-stronglyConnectedComponents
    val maxIterations=10//the maximum number of iterations to run for
    val cc2=graph.stronglyConnectedComponents(maxIterations).vertices
    cc2.foreach(print)
    println 


    val path2="/spark-2.0.0-bin-hadoop2.6/data/graphx/users.txt"
    val users=sc.textFile(path2).map{//map 中包含多行 必须使用{}    
      line=>val fields=line.split(",")
      (fields(0).toLong,fields(1))//(id,name) 多行书写 最后一行才是返回值 且与上行splitsplit(",")之间要有换行
    }    
    users.collect().foreach { println}
    println
    /*输出结果 (VertexId,name)
     * (1,BarackObama)
     * (2,ladygaga)
     * ...
     */


    val joint=cc.join(users)
    joint.collect().foreach { println}
    println

    /*输出结果
     * (VertexId,(cc,name))
     * (4,(1,justinbieber))
     * (6,(3,matei_zaharia))
     */

    val name_cc=joint.map{
      case (VertexId,(cc,name))=>(name,cc)
    }
    name_cc.foreach(print)   
    /*
     * (name,cc)
     * (BarackObama,1)(jeresig,3)(odersky,3)(justinbieber,1)(matei_zaharia,3)(ladygaga,1)
     */

  }  

}
```
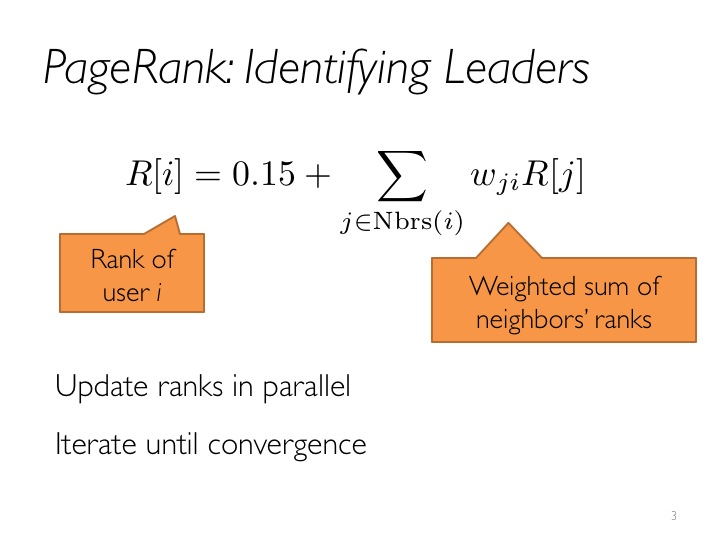
3.PageRank让链接来”投票”
一个页面的“得票数”由所有链向它的页面的重要性来决定，到一个页面的超链接相当于对该页投一票。一个页面的PageRank是由所有链向它的页面（“链入页面”）的重要性经过递归算法得到的。一个有较多链入的页面会有较高的等级，相反如果一个页面没有任何链入页面，那么它没有等级。
Spark Graphx实例直接参考：
http://www.cnblogs.com/shishanyuan/p/4747793.html
```
def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double]
//两个参数
//tol:the tolerance allowed at convergence (smaller => more accurate).
//tol越小计算结果越精确，但是会花更长的时间
//resetProb:the random reset probability (alpha)
//返回一个图，顶点的属性是PageRank(Double);边的属性是规范化的权重（Double）

Run a dynamic version of PageRank returning a graph with vertex attributes containing the PageRank and edge attributes containing the normalized edge weight.
```
```
val prGraph = graph.pageRank(tol=0.001).cache()
```
pregel
     在迭代计算中，释放内存是必要的，在新图产生后，需要快速将旧图彻底释放掉，否则，十几轮迭代后，会有内存泄漏问题，很快耗光作业缓存空间。但是直接使用Spark提供的API cache、unpersist和checkpoint，非常需要使用技巧。所以Spark官方文档建议：对于迭代计算，建议使用Pregal API，它能够正确的释放中间结果，这样就不需要自己费心去操作了。
     In iterative computations, uncaching may also be necessary for best performance.However, because graphs are composed of multiple RDDs, it can be difficult to unpersist them correctly. For iterative computation we recommend using the Pregel API, which correctly unpersists intermediate results.
        图是天然的迭代数据结构，顶点的属性值依赖于邻居的属性值，而邻居们的属性值同样也依赖于他们各自邻居属性值（即邻居的邻居）。许多重要的图算法迭代式的重新计算顶点的属性直到达到预设的迭代条件。这些迭代的图算法被抽象成一系列图并行操作。
     Graphs are inherently recursive data structures as properties of vertices depend on properties of their neighbors which in turn depend on properties of their neighbors. As a consequence many important graph algorithms iteratively recompute the properties of each vertex until a fixed-point condition is reached. A range of graph-parallel abstractions have been proposed to express these iterative algorithms. GraphX exposes a variant of the Pregel API.

     At a high level the Pregel operator in GraphX is a bulk-synchronous parallel messaging abstraction constrained to the topology of the graph. The Pregel operator executes in a series of super steps in which vertices receive the sum of their inbound messages from the previous super step, compute a new value for the vertex property, and then send messages to neighboring vertices in the next super step. Unlike Pregel, messages are computed in parallel as a function of the edge triplet and the message computation has access to both the source and destination vertex attributes. Vertices that do not receive a message are skipped within a super step. The Pregel operators terminates iteration and returns the final graph when there are no messages remaining.
Note, unlike more standard Pregel implementations, vertices in GraphX can only send messages to neighboring vertices and the message construction is done in parallel using a user defined messaging function. These constraints allow additional optimization within GraphX.
```
//Graphx 中pregel 所用到的主要优化：
1.   Caching for Iterative mrTriplets & Incremental Updates for Iterative mrTriplets ：在
很多图分析算法中，不同点的收敛速度变化很大。在迭代后期，只有很少的点会有更新。因此，对于没有更新的点，下一
次 mrTriplets 计算时 EdgeRDD 无需更新相应点值的本地缓存，大幅降低了通信开销。

2. Indexing Active Edges ：没有更新的顶点在下一轮迭代时不需要向邻居重新发送消息。因此， mrTriplets 
遍历边时，如果一条边的邻居点值在上一轮迭代时没有更新，则直接跳过，避免了大量无用的计算和通信。

3. Join Elimination ： Triplet 是由一条边和其两个邻居点组成的三元组，操作 Triplet 的 map 函数常常只
需访问其两个邻居点值中的一个。例如，在 PageRank 计算中，一个点值的更新只与其源顶点的值有关，而与其所指向
的目的顶点的值无关。那么在 mrTriplets 计算中，就不需要 VertexRDD 和 EdgeRDD 的 3-way join ，而只需
要 2-way join 。

所有这些优化使 GraphX 的性能逐渐逼近 GraphLab 。虽然还有一定差距，但一体化的流水线服务和丰富的编程接口，
可以弥补性能的微小差距。

//pregel 操作计算过程分析：
class GraphOps[VD, ED] {
  def pregel[A]
      //包含两个参数列表
      //第一个参数列表包含配置参数初始消息、最大迭代数、发送消息的边的方向（默认是沿边方向出）。
      //VD:顶点的数据类型。
      //ED:边的数据类型
      //A：Pregel message的类型。
      //graph：输入的图
      //initialMsg:在第一次迭代的时候顶点收到的消息。

maxIterations：迭代的次数

      (initialMsg: A,
       maxIter: Int = Int.MaxValue,
       activeDir: EdgeDirection = EdgeDirection.Out)

      //第二个参数列表包含用户 自定义的函数用来接收消息（vprog）、计算消息（sendMsg）、合并消息（mergeMsg）。 
      //vprog：用户定义的顶点程序运行在每一个顶点中，负责接收进来的信息，和计算新的顶点值。
      //在第一次迭代的时候，所有的顶点程序将会被默认的defaultMessage调用，
      //在次轮迭代中，顶点程序只有接收到message才会被调用。      
      (vprog: (VertexId, VD, A) => VD,//vprog：
      //sendMsg：用户提供的函数，应用于边缘顶点在当前迭代中接收message
      sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
      //用户提供定义的函数，将两个类型为A的message合并为一个类型为A的message
      mergeMsg: (A, A) => A)
    : Graph[VD, ED] = {

    // Receive the initial message at each vertex
    // 在第一次迭代的时候，所有的顶点都会接收到initialMsg消息，
    // 在次轮迭代的时候，如果顶点没有接收到消息，verteProgram(vprog)就不会被调用。
    var g = mapVertices( (vid, vdata) => vprog(vid, vdata, initialMsg) ).cache()

    // 使用mapReduceTriplets compute the messages（即map和reduce message，不断减少messages）
    var messages = g.mapReduceTriplets(sendMsg, mergeMsg)
    var activeMessages = messages.count()
    // Loop until no messages remain or maxIterations is achieved
    var i = 0
    while (activeMessages > 0 && i < maxIterations) {
      // Receive the messages and update the vertices.
      g = g.joinVertices(messages)(vprog).cache()
      val oldMessages = messages

      // Send new messages, skipping edges where neither side received a message. We must cache
      // messages so it can be materialized on the next line, allowing us to uncache the previous
      // iteration.
      messages = g.mapReduceTriplets(
        sendMsg, mergeMsg, Some((oldMessages, activeDirection))).cache()
      activeMessages = messages.count()
      i += 1
    }
    g
  }
}
整个过程不是很容易理解，更详细的计算过程分析可以参考：
Spark的Graphx学习笔记--Pregel：http://www.ithao123.cn/content-3510265.html
```
总之，把握住整个迭代过程：
vertexProgram（vprog）在第一次在初始化的时候，会在所有顶点上运行，之后，只有接收到消息的顶点才会运行vertexProgram，重复这个步骤直到迭代条件。
```
//计算最短路径代码
import org.apache.log4j.{Level, Logger}
import org.apache.spark.{SparkContext, SparkConf}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD

object myPregal {
  def main(args:Array[String]){

    //设置运行环境
    val conf = new SparkConf().setAppName("myGraphPractice").setMaster("local[4]")
    val sc=new SparkContext(conf)

    //屏蔽日志
    Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)    

    val vertexArray = Array(
      (1L, ("Alice", 28)),(2L, ("Bob", 27)),(3L, ("Charlie", 65)),(4L, ("David", 42)),
      (5L, ("Ed", 55)),(6L, ("Fran", 50))
    )
    //边的数据类型ED:Int
    val edgeArray = Array(
      Edge(2L, 1L, 7),Edge(2L, 4L, 2),Edge(3L, 2L, 4),Edge(3L, 6L, 3),
      Edge(4L, 1L, 1),Edge(5L, 2L, 2),Edge(5L, 3L, 8),Edge(5L, 6L, 3)
    )

    //构造vertexRDD和edgeRDD
    val vertexRDD: RDD[(Long, (String, Int))] = sc.parallelize(vertexArray)
    val edgeRDD: RDD[Edge[Int]] = sc.parallelize(edgeArray)

    //构造图Graph[VD,ED]
    val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)    


    val sourceId:VertexId=5//定义源点
    val initialGraph=graph.mapVertices((id,_)=>if (id==sourceId) 0 else Double.PositiveInfinity)  
    //pregel函数有两个参数列表
    val shorestPath=initialGraph.pregel(initialMsg=Double.PositiveInfinity,
                                        maxIterations=100,                                  
                                        activeDirection=EdgeDirection.Out)(

                                 //1-顶点属性迭代更新方式，与上一次迭代后保存的属性相比，取较小值
                                 //（将从源点到顶点的最小距离放在顶点属性中）    
                                 (id,dist,newDist)=>math.min(dist,newDist), 

                                 //2-Send Message，在所有能到达目的点的邻居中，计算邻居顶点属性+边属性
                                 //即（邻居-源点的距离+邻居-目的点的距离，并将这个距离放在迭代器中
                                 triplet=>{
                                   if(triplet.srcAttr+triplet.attr<triplet.dstAttr){
                                     Iterator((triplet.dstId,triplet.srcAttr+triplet.attr))
                                   }else{
                                     Iterator.empty
                                   }
                                 }, 

                                 //3-Merge Message，相当于Reduce函数
                                 //对所有能达到目的点的邻居发送的消息，进行min-reduce
                                 //邻居中最终reduce后最小的结果，作为newDist,发送至目的点，
                                 //至此，目的点中有新旧两个dist了，在下一次迭代开始的时候，步骤1中就可以进行更新迭代了
                                 (a,b)=>math.min(a,b))

    shorestPath.vertices.map(x=>(x._2,x._1)).top(30).foreach(print)  

    /*outprint(shorest distance,vertexId)
     * 8.0,3)(5.0,1)(4.0,4)(3.0,6)(2.0,2)(0.0,5)
     */ 
  }  
}
```
应用实例1：Louvain算法社区发现
      实例来自《Spark最佳实践》陈欢等著一书,整个这个实例可参考原书即可。
      源代码来自https://github.com/Sotera/spark-distributed-louvain-modularity git clone后就可以使用了。
      但是2.0版本Spark源码需要进行修改，因为老的聚合函数不能再使用了，需要修改成消息聚合函数，《Spark最佳实践》一书中已经进行了修改，可惜这本书没有给出完整的修改后代码，后面我会贴出修改的后的代码，替换git上的相应部分就可以使用了。
      社区发现算法可供参考的资料也比较多，算法也比较多。
http://blog.csdn.net/peghoty/article/details/9286905
关键概念–模块度（Modularity ）
      很多的社区发现算法都是基于模块度设计的，模块度用于衡量社区划分结构的合理性。
      用某种算法划分结果的内聚性与随机划分结果的内聚性的差值，对划分结果进行评估。
　　模块度是评估一个社区网络划分好坏的度量方法，它的物理含义是社区内节点的连边数与随机情况下的边数只差，它的取值范围是 [−1/2,1)，其定义如下：
Q=12m∑i,j[Aij−kikj2m]δ(ci,cj)

δ(u,v)={1when u==v0 else

　　其中，Aij节点i和节点j之间边的权重，网络不是带权图时，所有边的权重可以看做是1；ki=∑jAij表示所有与节点i相连的边的权重之和（度数）；ci表示节点i所属的社区；m=12∑ijAij表示所有边的权重之和（边的数目）。
　　公式中Aij−kikj2m=Aij−kikj2m，节点j连接到任意一个节点的概率是kj2m，现在节点i有ki的度数，因此在随机情况下节点i与j的边为kikj2m.
　　模块度的公式定义可以作如下简化：
　　
Q=12m∑i,j[Aij−kikj2m]δ(ci,cj)　　=12m[∑i,jAij−∑iki∑jkj2m]δ(ci,cj)　　=12m∑c[Σin−(Σtot)22m]
其中ΣinΣin表示社区c内的边的权重之和，ΣtotΣtot表示与社区c内的节点相连的边的权重之和。
　　上面的公式还可以进一步简化成:
Q=∑c[Σin2m−(Σtot2m)2]=∑c[ec−ac2]

　　这样模块度也可以理解是社区内部边的权重减去所有与社区节点相连的边的权重和，对无向图更好理解，即社区内部边的度数减去社区内节点的总度数。
　　基于模块度的社区发现算法，大都是以最大化模块度Q为目标。
Louvain算法流程
Louvain算法的思想很简单：
　　1）将图中的每个节点看成一个独立的社区，次数社区的数目与节点个数相同；
　　2）对每个节点i，依次尝试把节点i分配到其每个邻居节点所在的社区，计算分配前与分配后的模块度变化ΔQ ΔQ，并记录ΔQ ΔQ最大的那个邻居节点，如果maxΔQ>0 maxΔQ>0，则把节点i分配ΔQ ΔQ最大的那个邻居节点所在的社区，否则保持不变；
　　3）重复2），直到所有节点的所属社区不再变化；
　　4）对图进行压缩，将所有在同一个社区的节点压缩成一个新节点，社区内节点之间的边的权重转化为新节点的环的权重，社区间的边权重转化为新节点间的边权重；
　　5）重复1）直到整个图的模块度不再发生变化。
　　从流程来看，该算法能够产生层次性的社区结构，其中计算耗时较多的是最底一层的社区划分，节点按社区压缩后，将大大缩小边和节点数目，并且计算节点i分配到其邻居j的时模块度的变化只与节点i、j的社区有关，与其他社区无关，因此计算很快。
代码修改
由于版本的问题，Spark2.0中不再使用不稳定的mapReduceTriplets函数，替换为aggregateMessages。
```
(第1处修改）
def createLouvainGraph[VD: ClassTag](graph: Graph[VD,Long]) : Graph[VertexState,Long]与
def compressGraph(graph:Graph[VertexState,Long],debug:Boolean=true) : Graph[VertexState,Long]函数中：
//老版本
val nodeWeightMapFunc = (e:EdgeTriplet[VD,Long]) =>Iterator((e.srcId,e.attr), (e.dstId,e.attr))
val nodeWeightReduceFunc = (e1:Long,e2:Long) => e1+e2    
val nodeWeights = graph.mapReduceTriplets(nodeWeightMapFunc,nodeWeightReduceFunc)

//修改为:   
val nodeWeights = graph.aggregateMessages[Long](triplet=>
          (triplet.sendToSrc(triplet.attr),triplet.sendToDst(triplet.attr)),    
          (a,b)=>a+b)

（第2处修改）def louvain(sc:SparkContext...)函数中sendMsg函数：
//老版本
 private def sendMsg(et:EdgeTriplet[VertexState,Long]) = {
    val m1 = (et.dstId,Map((et.srcAttr.community,et.srcAttr.communitySigmaTot)->et.attr))
    val m2 = (et.srcId,Map((et.dstAttr.community,et.dstAttr.communitySigmaTot)->et.attr))
    Iterator(m1, m2)    
  }

//修改为
//import scala.collection.immutable.Map
private def sendMsg(et:EdgeContext[VertexState,Long,Map[(Long,Long),Long]]) = {    
      et.sendToDst(Map((et.srcAttr.community,et.srcAttr.communitySigmaTot)->et.attr))
      et.sendToSrc(Map((et.dstAttr.community,et.dstAttr.communitySigmaTot)->et.attr))     
  }  
```
使用新浪微博数据进行分析
详细分析可以参考《Spark最佳实践一书》
参考文献
（1）Spark 官方文档
http://spark.apache.org/docs/latest/graphx-programming-guide.html#pregel-api
（2）大数据Spark企业级实战王家林
（3）GraphX迭代的瓶颈与分析
http://blog.csdn.net/pelick/article/details/50630003
（4）基于Spark的图计算框架 GraphX 入门介绍
http://www.open-open.com/lib/view/open1420689305781.html
（5）Spark入门实战系列–9.Spark图计算GraphX介绍及实例
http://www.cnblogs.com/shishanyuan/p/4747793.html
（6）快刀初试：Spark GraphX在淘宝的实践
http://www.csdn.net/article/2014-08-07/2821097
（7）基于GraphX的社区发现算法FastUnfolding分布式实现
http://bbs.pinggu.org/thread-3614747-1-1.html
（8）关于图计算和graphx的一些思考
http://www.tuicool.com/articles/3MjURj
（9）用 LDA 做主题模型：当 MLlib 邂逅 GraphX
http://blog.jobbole.com/86130/
（10）Spark的Graphx学习笔记–Pregel
http://www.ithao123.cn/content-3510265.html
（11）Spark最佳实践陈欢林世飞
（12）社区发现(Community Detection)算法
http://blog.csdn.net/peghoty/article/details/9286905
正因为当初对未来做了太多的憧憬，所以对现在的自己尤其失望。生命中曾经有过的所有灿烂，终究都需要用寂寞来偿还。
查看全文

相关阅读:
open("","r")与open("","rb")的效率区别
 readline与readlines不能同时使用
 for i in xrange(0,5)使用过程中遇到的问题
 xrange()与range()
Maven install 、 Maven package 与 Maven clean package 的区别
 Java--mv clean package命令
 Java----如何解决下载依赖包失败问题
 Jmeter工具学习（六）-- 逻辑控制器 While Controller（转载）
Jmeter工具学习（五）--JDBC Request执行多条SQL语句
 Sqlmap POST注入三种方法（转载）

原文地址：https://www.cnblogs.com/candlia/p/11920130.html

Copyright © 2011-2022 走看看