标题:螺旋折线
如图p1.png所示的螺旋折线经过平面上所有整点恰好一次。
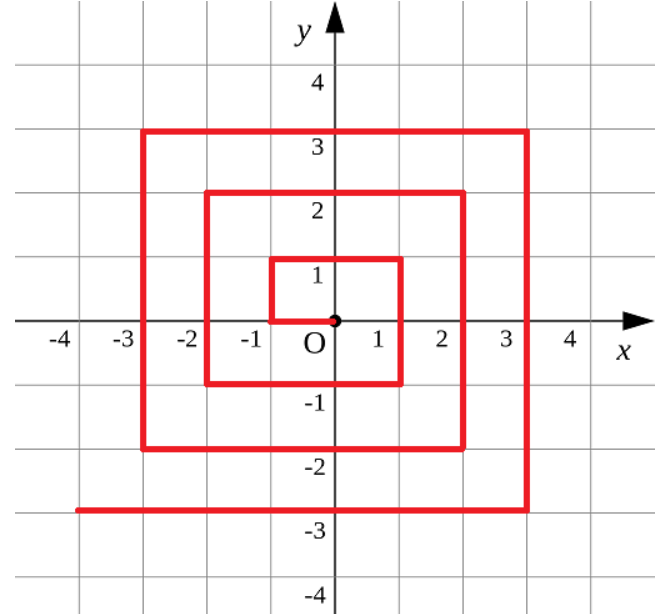
对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。
例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y),你能计算出dis(X, Y)吗?
【输入格式】
X和Y
X和Y
对于40%的数据,-1000 <= X, Y <= 1000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
【输出格式】
输出dis(X, Y)
输出dis(X, Y)
【样例输入】
0 1
【样例输出】
3
3
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms

1 #include <iostream> 2 #include <cmath> 3 using namespace std; 4 // x,y在对角线上 sat. -x = y 5 long long dialog_step(int x,int y) 6 { 7 long long n = 0; 8 if (y>0) 9 n = 2*y - 1; 10 else 11 n = 2*x; 12 return n*(n+1); 13 } 14 // step of any point 15 long long xy_step(int x, int y) 16 { 17 // split the space to 4 subspace 18 if (y>0 && (-y<=x && x<=y)) 19 { 20 // (-y,y) 21 long long step = dialog_step(-y,y)+(x+y); 22 return step; 23 } 24 if (x>0 && (-x<y && y<x)) 25 { 26 // (x,-x) 27 long long step = dialog_step(x,-x) - abs(-x-y); 28 return step; 29 } 30 if (y<0 && (-abs(y)<=x && x<= abs(y))) 31 { 32 // (-y,y) 33 long long step = dialog_step(-y,y) + abs(x-(-y)); 34 return step; 35 } 36 if (x<0 && (-abs(x)<y && y<abs(x))) 37 { 38 //(x,-x) 39 long long step = dialog_step(x,-x) - abs(-x-y); 40 return step; 41 } 42 } 43 int main() 44 { 45 // cout<<dialog_step(-1,1)<<endl; // 2 46 // cout<<dialog_step(1,-1)<<endl; // 6 47 // cout<<dialog_step(-2,2)<<endl; // 12 48 // cout<<dialog_step(2,-2)<<endl; // 20 49 cout<<xy_step(-1,0)<<endl; // 1 50 cout<<xy_step(-1,1)<<endl; // 2 51 cout<<xy_step(0,1)<<endl; // 3 52 cout<<xy_step(1,1)<<endl; // 4 53 cout<<xy_step(1,0)<<endl; // 5 54 cout<<xy_step(1,-1)<<endl; // 6 55 cout<<xy_step(0,-1)<<endl; // 7 56 cout<<xy_step(-1,-1)<<endl; // 8 57 cout<<xy_step(-2,-1)<<endl; // 9 58 cout<<xy_step(-2,0)<<endl; // 10 59 cout<<xy_step(1,-2)<<endl; // 21 60 cout<<xy_step(20,2)<<endl; // 21 61 return 0; 62 } 63
