算法原理
蝙蝠能够在夜间或十分昏暗的环境中自由飞翔和准确无误地捕捉食物,是因为他们能够从喉头发出地超声脉冲回声来定位。受这一启发,Yang教授在2010年提出了蝙蝠算法(Bat Algorithm,BA)[1]。
在蝙蝠算法中,为了模拟蝙蝠捕食猎物、避免障碍地随机搜索过程,做出如下三个近似理想化规则假设[2]:
(1) 种群中所有蝙蝠都利用回声定位的方法感知距离。
(2) 蝙蝠在位置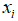 以速度
以速度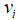 随机飞行,具有固定的频率
随机飞行,具有固定的频率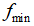 ,同时具有根据自身与猎物距离自动调整的波长
,同时具有根据自身与猎物距离自动调整的波长 和脉冲响度A。
和脉冲响度A。
(3) 假设脉冲响度的变化方式为从一个最大值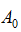 整数变化到固定最小值
整数变化到固定最小值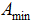 ,变化区间可根据问题调整。
,变化区间可根据问题调整。
假设蝙蝠搜索空间为D维,每一代中蝙蝠位置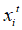 和速度
和速度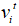 的更新规则如公式(1)~(3)所示。其中
的更新规则如公式(1)~(3)所示。其中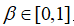 为一个随机变量。
为一个随机变量。 是群体当前局部最优解位置。
是群体当前局部最优解位置。
![]() (1)
(1)
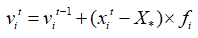 (2)
(2)
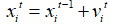 (3)
(3)
而局部搜索时,新的局部解使用随机游走方式生成,如公式(4)。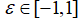 是一个随机数;
是一个随机数;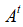 整个群体在同一代中的平均响度。在搜索过程中,蝙蝠会根据距离目标猎物的方位不断减小响度到一个定值的同时不断增大频度,将猎物范围缩小并捕食,在这一过程中,每只蝙蝠的声波响度和频度更新公式如(5)和(6)所示,其中
整个群体在同一代中的平均响度。在搜索过程中,蝙蝠会根据距离目标猎物的方位不断减小响度到一个定值的同时不断增大频度,将猎物范围缩小并捕食,在这一过程中,每只蝙蝠的声波响度和频度更新公式如(5)和(6)所示,其中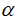 是声波响度衰减系数,值落在0到1之间不包含0和1;
是声波响度衰减系数,值落在0到1之间不包含0和1;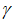 是脉冲频度增强系数大于0;
是脉冲频度增强系数大于0;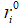 表示为蝙蝠
表示为蝙蝠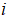 初始脉冲频率。
初始脉冲频率。
![]() (4)
(4)
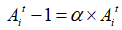 (5)
(5)
![]() (6)
(6)
蝙蝠算法的基本步骤为:
(1) 参数初始化:蝙蝠种群数量m,迭代次数N,目标函数f(x),蝙蝠位置![]() ,速度
,速度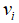 和声波频率
和声波频率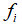 ,声波响度
,声波响度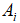 和频度
和频度 。
。
(2) 找出当前种群的最优位置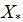 ,根据公式(2)~(4)更新位置和速度。
,根据公式(2)~(4)更新位置和速度。
(3) 生成[0,1]上的随机数rand1,如果rand1>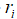 ,在最佳个体(解集)中选择一个最优个体(解),在选择的最优个体(解)周围根据公式(4)生成一个局部个体(解),否则根据公式(4)更新蝙蝠个体位置。
,在最佳个体(解集)中选择一个最优个体(解),在选择的最优个体(解)周围根据公式(4)生成一个局部个体(解),否则根据公式(4)更新蝙蝠个体位置。
(4) 生成[0,1]上的随机数rand2,如果rand2<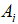 并且
并且 ,则接受该位置,根据公式(6)(7)减小
,则接受该位置,根据公式(6)(7)减小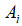 和增大
和增大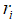 。
。
(5) 对该种群中所有个体适应度值进行排序,并找出当前最佳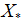 。
。
(6) 重复步骤(2)~(5),判断是否满足最大迭代次数,输出全局最优值。
参考文献
[1] X. S. Yang, A New Metaheuristic Bat-Inspired Algorithm, in: Nature Inspired Cooperative Strategies for Optimization (NISCO 2010), Studies in Computational Intelligence, Springer Berlin, 284, Springer, 65-74 (2010). http://arxiv.org/abs/1004.4170
[2] XU Degang, ZHAO Ping. Literature Survey on Research and Application of Bat Algorithm. CEA, 2019, 55(15): 1-12.
参考代码
1.https://www.mathworks.com/matlabcentral/fileexchange/44707-binary-bat-algorithm