一、定义
Eg.一个保存了8个单词的字典树的结构如下图所示,8个单词分别是:“A”,“to”,“tea”,“ted”,“ten”,“i” ,“in”,“inn”。
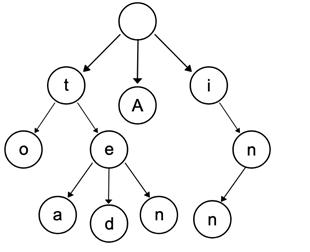
- 字典(Trie)树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种。
- 应用:统计和排序大量的字符串(但不仅限于字符串),经常被搜索引擎系统用于文本词频统计、前缀匹配用来搜索提示,也常用于计算左右信息熵、计算点互信息等,进阶版可与默克尔树融合成Merkle Patricia Tree用于区块链。
- 优点:最大限度地减少无谓的字符串比较,利用字符串的公共前缀来降低查询时间,空间换时间,因而查询效率高。
- 缺点:如果大量字符串没有共同前缀时很耗内存。
- 性质
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
- 时间复杂度:创建时间复杂度为O(L),查询时间复杂度是O(logL),查询时间复杂度最坏情况下是O(L),L是字符串的长度。
二、基本操作(创建、插入和查找)
1 class TrieNode: 2 def __init__(self): 3 # 创建字典树的节点 4 self.nodes = dict() 5 self.is_leaf = False 6 7 def insert(self, word: str): 8 """ 9 基本操作:插入 10 Parameters 11 ---------- 12 word : str 13 Returns 14 ------- 15 None. 16 17 """ 18 curr = self 19 for char in word: 20 if char not in curr.nodes: 21 curr.nodes[char] = TrieNode() 22 curr = curr.nodes[char] 23 curr.is_leaf = True 24 def search(self, word: str): 25 """ 26 基本操作:查找 27 Parameters 28 ---------- 29 word : str 30 31 Returns 32 ------- 33 34 """ 35 curr = self 36 for char in word: 37 if char not in curr.nodes: 38 return False 39 curr = curr.nodes[char] 40 return curr.is_leaf
三、应用实例
1 class TrieNode(object): 2 def __init__(self, value=None, count=0, parent=None): 3 # 值 4 self.value = value 5 # 频数统计 6 self.count = count 7 # 父节点 8 self.parent = parent 9 # 子节点,{value: TrieNode} 10 self.children = {} 11 12 class Trie(object): 13 def __init__(self): 14 # 创建空的根节点 15 self.root = TrieNode() 16 17 def insert(self, sequence): 18 """ 19 基本操作:插入一个单词序列 20 :param sequence:列表 21 :return: 22 """ 23 cur_node = self.root # 当前节点 24 for item in sequence: #遍历单词的每一个字符 25 if item not in cur_node.children: # 当前字符不在当前节点的子节点中 26 # 插入节点 27 child = TrieNode(value=item, count=1, parent=cur_node) # 新建节点 28 cur_node.children[item] = child # 将该节点接入当前节点的子节点 29 cur_node = child # 当前节点更新为子节点 30 else: 31 # 更新节点 32 cur_node = cur_node.children[item] # 更新当前节点为已存在的子节点 33 cur_node.count += 1 # 当前节点的计数+1 34 35 def search(self, sequence): 36 """ 37 基本操作,查询是否存在完整序列 38 39 Parameters 40 ---------- 41 sequence : 列表 42 43 Returns: 44 45 """ 46 cur_node = self.root # 根节点 47 mark = True # 标记是否找到 48 for item in sequence: # 遍历序列 49 if item not in cur_node.children: # 判断子结点中是否存在 50 mark = False 51 break 52 else: # 存在 53 cur_node = cur_node.children[item] # 更新当前节点 54 # 如果还有子节点,说明序列并非完整,则查找不成功【此处可视情况找到前缀即反馈成功】 55 if cur_node.children: 56 mark = False 57 return mark 58 59 def delete(self, sequence): 60 """ 61 基本操作,删除序列,准确来说是减少计数 62 63 Parameters 64 ---------- 65 sequence : 列表 66 67 Returns 68 69 """ 70 mark = False 71 if self.search(sequence): 72 mark = True 73 cur_node = self.root # 获取当前节点 74 for item in sequence: # 遍历序列 75 cur_node.children[item].count -= 1 # 节点计数减1 76 if cur_node.children[item].count == 0: # 如果节点计数为0 77 cur_node.children.pop(item) # 删除该节点 78 break 79 else: 80 cur_node = cur_node.children[item] # 更新当前节点 81 return mark 82 83 def search_part(self, sequence, prefix, suffix, start_node=None): 84 """ 85 递归查找子序列,返回前缀和后缀节点(此处仅返回前后缀的内容与频数) 86 87 Parameters 88 ---------- 89 sequence : 列表 90 DESCRIPTION. 91 prefix : TYPE 92 前缀字典,初始传入空字典 93 suffix : TYPE 94 后缀字典,初始传入空字典 95 start_node : TYPE, optional 96 起始节点,用于子树的查询 97 98 Returns 99 ------- 100 None. 101 102 """ 103 if start_node: # 该节点不为空,获取第一个子结点 104 cur_node = start_node 105 prefix_node = start_node.parent 106 else: # 定位到根节点 107 cur_node = self.root 108 prefix_node = self.root 109 mark = True 110 # 必须从第一个结点开始对比 111 for i in range(len(sequence)): 112 if i == 0: 113 if sequence[i] != cur_node.value: # 第一个节点不相同,找到第一个相同值的节点 114 for child_node in cur_node.children.values(): # 该节点的每一个分支递归查找 115 self.search_part(sequence, prefix, suffix, child_node) 116 mark = False 117 break 118 else: 119 if sequence[i] not in cur_node.children: # 后序列中值不在当前节点孩子中 120 for child_node in cur_node.children.values(): 121 self.search_part(sequence, prefix, suffix, child_node) 122 mark = False 123 break 124 else: 125 cur_node = cur_node.children[sequence[i]] # 继续查找序列 126 if mark: # 找到序列 127 if prefix_node.value in prefix: # 当前节点加入序列中 128 prefix[prefix_node.value] += cur_node.count 129 else: 130 prefix[prefix_node.value] = cur_node.count 131 for suffix_node in cur_node.children.values(): 132 if suffix_node.value in suffix: 133 suffix[suffix_node.value] += suffix_node.count 134 else: 135 suffix[suffix_node.value] = suffix_node.count 136 # 即使找到一部分还需继续查找子节点 137 for child_node in cur_node.children.values(): 138 self.search_part(sequence, prefix, suffix, child_node) 139 140 if __name__ == "__main__": 141 trie = Trie() 142 texts = [["葬爱", "少年", "葬爱", "少年", "慕周力", "哈哈"], ["葬爱", "少年", "阿西吧"], ["烈", "烈", "风", "中"], ["忘记", "了", "爱"], 143 ["埋葬", "了", "爱"]] 144 145 for text in texts: 146 trie.insert(text) 147 markx = trie.search(["忘记", "了", "爱"]) 148 print(markx) 149 markx = trie.search(["忘记", "了"]) 150 print(markx) 151 markx = trie.search(["忘记", "爱"]) 152 print(markx) 153 markx = trie.delete(["葬爱", "少年", "王周力"]) 154 print(markx) 155 prefixx = {} 156 suffixx = {} 157 trie.search_part(["葬爱", "少年"], prefixx, suffixx) 158 print(prefixx) 159 print(suffixx)
参考文献
[1]. 百度百科词条【字典树】:https://baike.baidu.com/item/字典树/9825209
[2]. 看动画轻松理解「Trie树」,https://www.cxyxiaowu.com/1873.html
[3]. 字典树python实现,https://blog.csdn.net/danengbinggan33/article/details/82151220
[4]. 吐血攻略Trie,包教包会,https://leetcode-cn.com/problems/short-encoding-of-words/solution/99-java-trie-tu-xie-gong-lue-bao-jiao-bao-hui-by-s/