二分搜索基础

一、二分搜索模板

简单模板代码：

    public static int binarySearch(int[] array, int target) {
        if (array == null || array.length == 0) {
            return -1;
        }

        int start = 0;
        int end = array.length - 1;
        int middle;
        // 相邻 start = end - 1 或者 start = end
        while (start + 1 < end) { // (1)
            middle = start + (end - start) / 2; // (2)
            if (array[middle] == target) {
                return middle;
            } else if (array[middle] < target) {
                //target在右边
                start = middle;
            } else {
                end = middle;
            }
        }
        if (array[start] == target) {  // (3)
            return start;
        } else if (array[end] == target) { // (4)
            return end;
        } else {
            return -1;
        }
    }

说明:

(1) (start+end)/2 在start+end的值较大的时候有可能会超出范围, 因此这里使用start+(end-start)/2

(2) 为什么使用start+1<end? 为了防止死循环:

　　循环终止条件为:start+1>=end, 即相邻或者相交的情况

(3) (4) : 在相邻或者相交的情况下都终止, 再判断可以简单防止死循环

二、二分查找区间

问题描述: http://www.lintcode.com/en/problem/search-for-a-range/

即给定一个有序的数组和target value, 寻找target value的起始和结束位置, 不存在就返回(-1,-1);

思路: 二分搜索的扩展.

(1) 分二次查找

(2) 结束条件都是相邻或者相交

(3) 找左边界就是start->end

(4) 找右边界就是end->start

public class BinarySearch {

    public static void main(String[] args) {
        int[] array = new int[]{1, 2, 3, 4, 4 ,4, 4, 5};
        System.out.println(Arrays.toString(binarySearch(array, 4)));
    }

    public static int[] binarySearch(int[] array, int target) {
        if (array == null || array.length == 0) {
            return new int[]{-1, -1};
        }

        int start = 0;
        int end = array.length - 1;
        // left是左边的, right是右边的
        int middle, left, right;

        // 相邻 start = end - 1 或者 start = end
        while (start + 1 < end) {
            middle = start + (end - start) / 2;
            if (array[middle] == target) {
                end = middle;
            } else if (array[middle] < target) {
                //target在右边
                start = middle;
            } else {
                end = middle;
            }
        }

        if (array[start] == target) {
            left = start;
        } else if (array[end] == target) {
            left = end;
        } else {
            return new int[]{-1, -1};
        }

        start = 0;
        end = array.length - 1;
        middle = 0;

        while (start + 1 < end) {
            middle = start + (end - start) / 2;
            if (array[middle] == target) {
                start = middle;
            } else if (array[middle] < target) {
                //target在右边
                start = middle;
            } else {
                end = middle;
            }
        }

        if (array[end] == target) {
            right = end;
        } else if (array[start] == target) {
            right = start;
        } else {
            return new int[]{-1, -1};
        }
        return new int[]{left, right};
    }

}

三、二分查找插入位置

问题描述：

http://www.lintcode.com/en/problem/search-insert-position/

(1) 给一个有序的数组

(2) 寻找插入位置

二分查找的精髓: 每次去掉一半, 最后剩下的情况就是start=end或者start+1=end, 而无论哪种都可以当做start+1=end考虑;

   public static int searchInsert(int[] A, int target) {
        if (A == null || A.length == 0) {
            return 0;
        }
        int start = 0, end = A.length - 1;

        while (start + 1 < end) {
            int mid = start + (end - start) / 2;
            if (A[mid] == target) {
                return mid;
            } else if (A[mid] < target) {
                start = mid;
            } else {
                end = mid;
            }
        }

        if (A[start] >= target) {
            return start;
        } else if (A[end] >= target) {
            return end;
        } else {
            return end + 1;
        }
    }

四、循环数组二分查找

问题描述:

http://www.lintcode.com/en/problem/search-in-rotated-sorted-array/

Suppose a sorted array is rotated at some pivot unknown to you beforehand.

(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

循环数组的二分查询，画图2个象限，简单的分类讨论感觉用代码实现也很麻烦.

这里说一下思路:

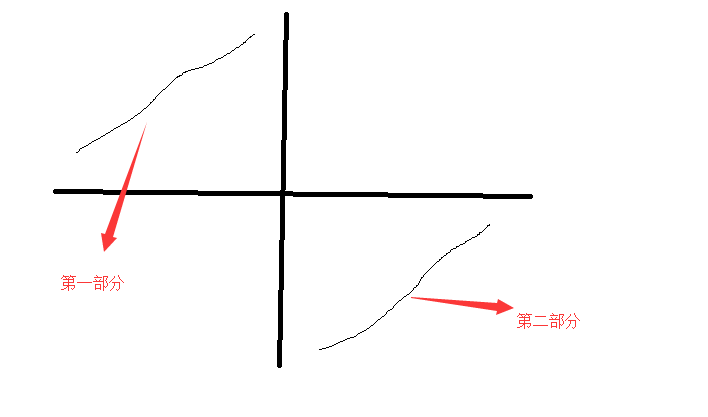
(1) 首先判断mid在第一部分和第二部分

(2) 将问题细化, 这里只考虑第一部分:

　　如果A[start] < A[end], 则是一般情况

　　否则 start, mid ,end将数组分为了3个区间, A[mid]<=target<=A[end]则说明target在mid和end中间, 否则是start,mid中.

(3) 第二部分类似

(4) 问题解决

    public static int search(int[] A, int target) {
        if (A == null || A.length == 0) {
            return -1;
        }
        int start = 0, end = A.length - 1;
        int mid;
        while (start + 1 < end) {
            mid = start + (end - start) / 2;
            if (A[mid] == target)
                return mid;
            // 分为2大类: 在哪边？
            if (A[mid] > A[start]) {
                if (A[end] >= A[start]) {
                    //..
                    if (A[mid] > target) {
                        end = mid;
                    } else {
                        start = mid;
                    }
                } else {
                    if (target >= A[start] && target <= A[mid]) {
                        end = mid;
                    } else {
                        start = mid;
                    }
                }
            } else {
                if (A[start] <= A[end]) {
                    if (A[mid] > target) {
                        end = mid;
                    } else {
                        start = mid;
                    }
                } else {
                    if (target >= A[mid] && target <=A[end]){
                        start = mid;
                    }else {
                        end = mid;
                    }
                }
            }


        }
        if (A[start] == target) {
            return start;
        } else if (A[end] == target) {
            return end;
        } else {
            return -1;
        }
    }

五、矩阵二分搜索

问题描述, 非常简单, 一个矩阵m*n 可以用数组表示:

　　(1) 没一行都有序

　　(2) 第n+1行比第n行的都大

例如:

[
    [1, 3, 5, 7],
    [10, 11, 16, 20],
    [23, 30, 34, 50]
]

非常简单, 看成是一个数组就可以..

    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0) {
            return false;
        }
        if (matrix[0] == null || matrix[0].length == 0) {
            return false;
        }

        int row = matrix.length, column = matrix[0].length;
        int start = 0, end = row * column - 1;

        while (start + 1 < end) {
            int mid = start + (end - start) / 2;
            int number = matrix[mid / column][mid % column];
            if (number == target) {
                return true;
            } else if (number < target) {
                start = mid;
            } else {
                end = mid;
            }
        }

        if (matrix[start / column][start % column] == target) {
            return true;
        } else if (matrix[end / column][end % column] == target) {
            return true;
        }

        return false;
    }

下面考虑更为复杂的情况:

(1) 每一行都是有序的

(2) 每一列都是有序的要怎么做?

这里说明一下思路:

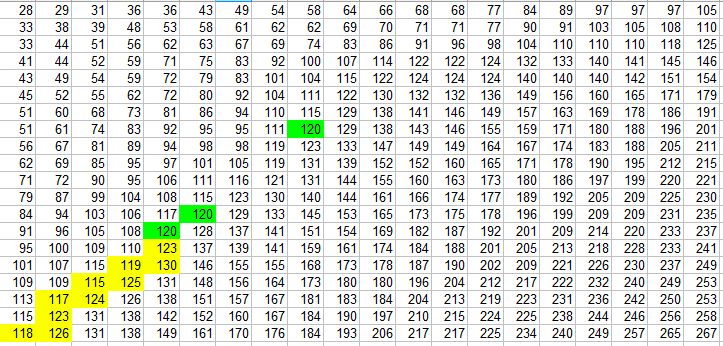
从左下方开始判断, 如果target < matirx[i][j], 说明第i列的数都没用, i++

如果target > matirx[i][j], 说明第j列的数都没有用, j++. 

六、合并有序数组

合并有序数组非常简单, 但是假设这样的情况: A中有足够的位置去合并, 不能创建新的数组要怎么办 ?

A = [1, 2, 3, empty, empty], B = [4, 5]

After merge, A will be filled as [1, 2, 3, 4, 5]

思路非常简单, 看empty在哪边? 这里从后面开始扩展就可以~

代码如下: 这里也是创建了新数组C, 然后把A拷贝进去模拟A中有足够的位置：

    public static void main(String[] args) {
        merge(
                new int[]{1, 3, 4},
                new int[]{2, 3, 5, 8, 9}
        );
    }

    public static void merge(int[] A, int B[]) {
        int[] C = new int[A.length + B.length];
        System.arraycopy(A, 0, C, 0, A.length);
        int a = A.length - 1;
        int b = B.length - 1;
        int i = a + b + 1;
        while (i >= 0 && a >= 0 && b >= 0) {
            if (A[a] > B[b]) {
                C[i] = A[a];
                a--;
            } else {
                C[i] = B[b];
                b--;
            }
            i--;
        }
        if (b < 0) {
            //a 剩下
            System.arraycopy(A, 0, C, 0, a + 1);
        } else if (a < 0) {
            System.arraycopy(B, 0, C, 0, b + 1);
        }

        System.out.println(Arrays.toString(C));
    }

七、2个有序数组寻找kth问题

(1) 2个有序数组

(2) 寻找2个数组加起来第k个

(3) 要求是算法复杂度是log(m+n)

思路是什么：要log的时间复杂度，每次必须抛弃一半:

只要每次比较 A[k/2]和B[k/2]就可以, 如果A[k/2]<B[k/2]就可以抛弃A中的k/2个元素...

代码如下(没有经过充分测试)：

  public static void main(String[] args) {
        int[] A = {1, 2, 3, 4, 5, 6};
        int[] B = {2, 3, 4, 5};
        System.out.println(findMedianSortedArrays(A, B));
    }

    public static double findMedianSortedArrays(int A[], int B[]) {
        int len = A.length + B.length;
        if (len % 2 == 1) {
            return findKth(A, 0, B, 0, len / 2 + 1);
        }
        return (
                findKth(A, 0, B, 0, len / 2) + findKth(A, 0, B, 0, len / 2 + 1)
        ) / 2.0;
    }

    /**
     * @param A       数组A
     * @param A_start 数组A起始位置
     * @param B       数组B
     * @param B_start 数组B起始位置
     * @param k       寻找第K个数
     * @return
     */
    public static int findKth(int[] A, int A_start, int[] B, int B_start, int k) {

        if (A_start > A.length - 1) {
            return B[B_start + k - 1];
        }
        if (B_start > B.length - 1) {
            return A[A_start + k - 1];
        }
        //

        if (k == 1) {
            return Math.min(A[A_start], B[B_start]);
        }
        // 要考虑k/2超出边界的情况
        int a_new_start = A_start + k / 2 - 1;
        int b_new_start = B_start + k / 2 - 1;
        int a_length, b_length;
        if (a_new_start > A.length - 1) {
            a_new_start = A.length - 1;
        }
        a_length = a_new_start - A_start + 1;
        if (b_new_start > B.length - 1) {
            b_new_start = B.length - 1;
        }
        b_length = b_new_start - B_start + 1;

        if (A[a_new_start] < B[b_new_start]) {
            //A这边小一点, 全面的全部被抛弃
            return findKth(A, a_new_start + 1, B, B_start, k - a_length);
        } else {
            return findKth(A, A_start, B, b_new_start + 1, k - b_length);
        }
    }