网址链接:https://algorithms.tutorialhorizon.com/dynamic-programming-edit-distance-problem/
1. 目标:给定两个字符串s1, s2,写出一个算法来找出从s1转化到s2所需要的最小操作步骤数(编辑距离)。
所允许的操作:
-
Insert(插入)——插入一个新的字符
-
delete(删除)——删除一个字符
-
s1 = "horizon"
s2 = "horzon"
Output: 1 {remove 'i' from string s1}
s1 = "horizon"
s2 = "horizontal"
Output: 3 {insert 't', 'a', 'l' characters in string s1}
同时比较两个字符串中的一个字符。在这里,我们从右到左(从后到前backwards)比较字符串。
现在对于每个字符串,我们有两种选择:
-
如果两个字符串中的最后一个字符是相同的,则忽略最后这个字符,然后再同时比较倒数第二个字符,一直比较下去,知道两个字符相同,就进入第二种情况(类似于递归的解决剩余的字符)
-
如果两个字符串中的最后一个字符不相同,那么就尝试上述三种操作(insert,replace,delete)使得最后一个字符相同。并且为每种可能性递归获取剩余字符串的解决方案,并从中选择最小值。
假设给定的字符串分别是s1和s2,长度分别为m和n:
case1:最后一个字符相同,递归的求解剩余的m-1,n-1个字符
case2:最后一个字符不相同,然后递归尝试所有可能的操作。
-
将一个字符插入s1中(插入的字符要与字符串s2中的最后一个字符相同,以便两个字符串中的最后一个字符相同):现在s1的长度将为m + 1,s2的长度为n,忽略最后一个字符并递归求解剩余的m,n -1个字符。
-
从字符串s1中删除最后一个字符。现在s1长度将是m-1,s2长度为n,递归求解m-1,n。
-
将最后一个字符替换为s1(与字符串s2中的最后一个字符相同,以便两个字符串中的最后一个字符相同):s1的长度为m,s2的长度为n,忽略最后一个字符,然后递归求解m-1,n- 1。
# 基于递归的解决方法
def edit_dist(str1, str2, m, n):
if m == 0:
return n
if n == 0:
return m
if str1[m-1] == str2[n-1]:
return edit_dist(str1, str2, m-1, n-1)
return 1 + min(edit_dist(str1, str2, m, n-1),
edit_dist(str1, str2, m-1, n),
edit_dist(str1, str2, m-1, n-1))
s1 = "horizon"
s2 = "horizontal"
print(edit_dist(s1, s2, len(s1), len(s2)))
输出结果:
3
让我们分析上述解决方案。 在最坏的情况下,我们需要对字符串的每个字符执行操作,因为我们有3次操作,所以时间复杂度将为O(3 ^ n)。
让我们看看是否存在重叠的子问题。例: 字符串s1:“ CAT”,字符串s2:“ DOG”
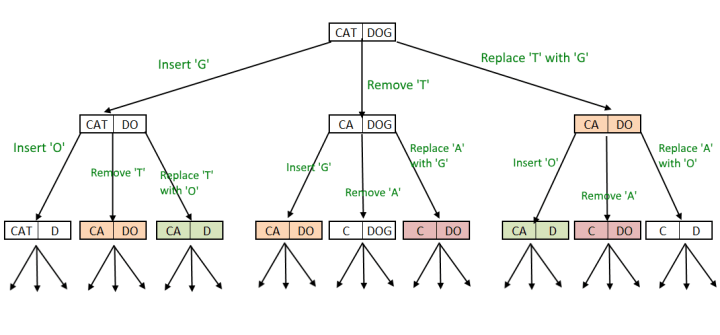
正如我们看到的那样,有很多子问题可以反复解决,因此在这里有很多重叠的子问题。我们可以通过自底向上的方式使用动态编程来解决它。 我们将解决问题并将其存储到数组中(维护数组),并根据需要使用解决方案,以确保每个子问题仅被解决一次。
# 基于动态规划的解法
def dp_edit_dist(str1, str2):
# m,n分别字符串str1和str2的长度
m, n = len(str1), len(str2)
# 构建二位数组来存储子问题(sub-problem)的答案
dp = [[0 for x in range(n+1)] for x in range(m+1)]
# 利用动态规划算法,填充数组
for i in range(m+1):
for j in range(n+1):
# 假设第一个字符串为空,则转换的代价为j (j次的插入)
if i == 0:
dp[i][j] = j
# 同样的,假设第二个字符串为空,则转换的代价为i (i次的插入)
elif j == 0:
dp[i][j] = i
# 如果最后一个字符相等,就不会产生代价
elif str1[i-1] == str2[j-1]:
dp[i][j] = dp[i-1][j-1]
# 如果最后一个字符不一样,则考虑多种可能性,并且选择其中最小的值
else:
dp[i][j] = 1 + min(dp[i][j-1], # Insert
dp[i-1][j], # Remove
dp[i-1][j-1]) # Replace
return dp[m][n]
注释:
在计算机科学中,编辑距离是一种通过计算将一个字符串转换为另一个字符串所需的最小操作数量来量化两个字符串(例如单词)彼此之间有多不同的方式。编辑距离可以在自然语言处理中找到应用之处,如其中自动拼写校正可以通过从字典中选择与所讨论单词的距离较小的单词来确定拼写错误的单词的对其进行更正。在生物信息学中,它可以用于量化DNA序列的相似性,可以将其视为字母A,C,G和T的字符串。