一般来说,我们解决向量旋转问题一般要么是用旋转矩阵,要么是用四元数。但很早以前我从网上找了一种比较另类的函数,当时也没有深究。最近又把这个函数拿出看看,仔细一琢磨,发现真的很另类。这里分享一下,就当是扩展一下思维。这个旋转方法据说叫Rodrigues旋转公式。
这个方法的公式是这样的,P'=P·cosθ + (A×P)sinθ +A(A·P)(1 - cosθ)。这种公式任谁第一眼看到都会摸不着头脑,我们首先来将公式换一个写法:
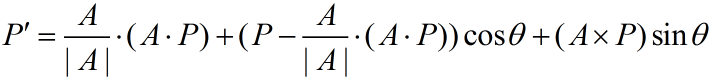
图1
这个公式中|A|=1。为什么这样变换呢?因为P'正好是三个向量相加,后面会详细分析的,我们先将假设P'=u1+u2+u3。接下来我们分析每一项具体是什么。如图2所示,P绕A轴旋转θ角,其中θ角如图位置。φ角是向量P和轴A之间的夹角。u1是向量P在A轴的投影,u2是向量(P'-u1)在向量(P-u1)的投影,u3是从u2末端到P'的向量,垂直于u2。
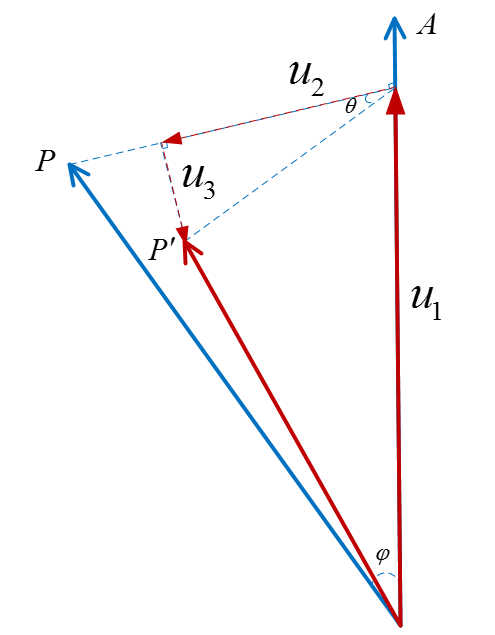
图2
u1的公式如下:
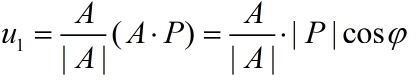
图3
其中|A|=1,u2的公式如下:
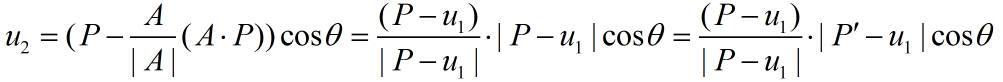
图4
其中|P-u1|=|P'-u1|,u3的公式如下:
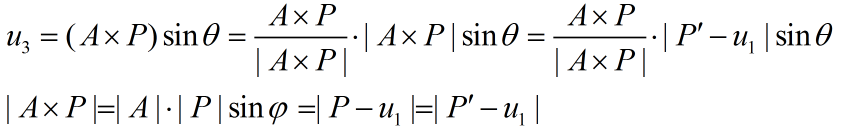
图5
其中公式已经很清楚的阐述了推理过程,下面贴出实现的函数代码。
void rotateWithAxis(CVector3& rotate, CVector3& axis, GLdouble angle, CVector3& direct)
{
/*
P绕A轴旋转角度θ,得到新的向量P',则:
P'=P * cosθ + (A×P)sinθ +A(A·P)(1 - cosθ)
其中A为单位向量,旋转角度θ为"逆时针方向"旋转的角度。
rotate 表示的是向量P
axis 表示的是轴A
angle 表示的是角度θ
direct 表示的是向量P'
A×P=(ay * pz- az * py, ax * pz- az * px , ax * py- ay * px)
A·P = ax * px + ay * py + az * pz
*/
#define PI 3.1415926535898
#define Cos cos(anglePI)
#define Sin sin(anglePI)
GLdouble anglePI = angle/180 * PI;
CVector3 cross;
GLdouble s;
axis.Normal();
cross = CVector3::Cross(rotate, axis);
s = rotate[0]*axis[0] + rotate[1]*axis[1] + rotate[2]*axis[2];
direct.SetVector3(rotate[0]*Cos + cross[0]*Sin + axis[0]*s*(1-Cos),
rotate[1]*Cos + cross[1]*Sin + axis[1]*s*(1-Cos), rotate[2]*Cos + cross[2]*Sin + axis[2]*s*(1-Cos));
}