一 概念
函数式编程（英语：Functional programming），又称泛函编程，是一种编程范型，它将电脑运算视为数学上的函数计算，并且避免状态以及可变数据。函数编程语言最重要的基础是 λ 演算（lambda calculus）。而且λ演算的函数可以接受函数当作输入（引数）和输出（传出值）。代表语言haskell,erlang，lisp等
特点：
（1）函数式编程经常使用递归。
（2）纯函数式的程序不可变量和无副作用(Side effect)。因为纯函数式程序设计语言没有变量，函数没有副作用，编写出的程序可以利用记忆化、公共子表达式消除和并发计算在运行时和编译时得到大量优化。
（3）惰性求值
(4) 高阶函数
（5）一切皆函数
缺点：速度和空间上的顾虑
函数式编程常被认为严重耗费在CPU和存储器资源。主因有二：
- 早期的函数式编程语言实现时并无考虑过效率问题。
- 非函数式编程语言为求提升速度，会在某些部分放弃边界检查或垃圾回收等功能。
二 λ演算
λ演算（lambda calculus）是一套用于研究函数定义、函数应用和递归的形式系统。Lambda演算被称为最小的通用程序设计语言。它包括一条变换规则（变量替换）和一条函数定义方式，Lambda演算之通用在于，任何一个可计算函数都能用这种形式来表达和求值。因而，它是等价于图灵机的。尽管如此，Lambda演算强调的是变换规则的运用，而非实现它们的具体机器。可以认为这是一种更接近软件而非硬件的方式。
形式化定义
所有的lambda表达式可以通过下述以BNF范式表达的上下文无关文法描述：
- <expr> ::= <identifier>
- <expr> ::=(λ<identifier> .<expr>)
- <expr> ::=(<expr> <expr>)
头两条规则用来生成函数，而第三条描述了函数是如何作用在参数上的。
如下假定保证了不会产生歧义：（1）函数的作用是左结合的，和（2）lambda操作符被绑定到它后面的整个表达式。例如，表达式 (λx.x x)(λy.y) 可以简写成λ(x.x x) λy.y 。三 lambda演算中的算术
1 邱奇数
Church 编码是把数据和运算符嵌入到 lambda 演算内的一种方式，最常见的形式是 Church 数，它是使用 lambda 符号的自然数的表示法。这种方法得名于 Alonzo Church，他首先以这种方法把数据编码到 lambda 演算中。
在其他符号系统中通常被认定为基本的项(比如整数、布尔值、有序对、列表和 tagged unions)都被映射到使用 Church 编码的高阶函数；根据邱奇-图灵论题我们知道任何可计算的运算符(和它的运算数)都可以用 Church 编码表示。
很多学数学的学生熟悉可计算函数集合的哥德尔编号；Church
编码是定义在 lambda
抽象而不是自然数上的等价运算。
Church 数
Church 数是在 Church 编码下的自然数的表示法。表示自然数 
的高阶函数是把任何其他函数 
映射到它的 n 重函数复合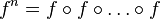 
的函数。
定义
Church 数 0, 1, 2, ... 在 lambda 演算中被定义如下:
-
0 ≡
λf.λx. x -
1 ≡
λf.λx. f x -
2 ≡
λf.λx. f (f x) -
3 ≡
λf.λx. f (f (f x)) - ...
-
n ≡
λf.λx. fn x - ...
就是说，自然数 被表示为 Church 数 n，它对于任何 lambda-项 F和 X 有着性质：
-
n
F X=βFn X。
使用 Church 数的计算
在 lambda 演算中，数值函数被表示为在 Church 数上的相应函数。这些函数在大多数函数式语言中可以通过 lambda 项的直接变换来实现(服从于类型约束)。
加法函数 
利用了恒等式 
。
-
plus ≡
λm.λn.λf.λx. m f (n f x)
后继函数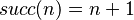 
β-等价于
(plus 1)。
-
succ ≡
λn.λf.λx. f (n f x)
乘法函数 
利用了恒等式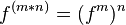 
。
-
mult ≡
λm.λn.λf. n (m f)
指数函数 
由 Church 数定义直接给出。
-
exp ≡
λm.λn. n m
前驱函数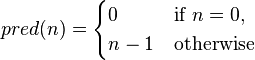 
通过生成每次都应用它们的参数 g 于 f 的 重函数复合来工作；基础情况丢弃它的 f 复本并返回 x。
-
pred ≡
λn.λf.λx. n (λg.λh. h (g f)) (λu. x) (λu. u)
Church 布尔值
Church 布尔值是布尔值真和假的 Church 编码。布尔值被表示为两个参数的函数，它得到这两个参数中的一个。
lambda 演算中的形式定义:
-
true ≡
λa.λb. a -
false ≡
λa.λb. b
从Church 布尔值推导来的布尔算术的函数:
-
and ≡
λm.λn.λa.λb. m (n a b) b -
or ≡
λm.λn.λa.λb. m a (n a b) -
not ≡
λm.λa.λb. m b a
有序对
有序对（2-元组）数据类型可以用TRUE、FALSE和IF来定义。
- CONS := λx y.λp.IF p x y
- CAR := λx.x TRUE
- CDR := λx.x FALSE
链表数据类型可以定义为，要么是为空列表保留的值（e.g.FALSE），要么是CONS一个元素和一个更小的列表。
递归
递归是使用函数自身的函数定义；在表面上，lambda演算不允许这样。但是这种印象是误解。考虑个例子，阶乘函数f(n)递归的定义为
- f(n):= if n = 0 then 1 else n·f(n-1)。
在lambda演算中，你不能定义包含自身的函数。要避免这样，你可以开始于定义一个函数，这里叫g，它接受一个函数f作为参数并返回接受n作为参数的另一个函数：
- g := λf n.(if n = 0 then 1 else n·f(n-1))。
函数g返回要么常量1，要么函数f对n-1的n次应用。使用ISZERO谓词，和上面描述的布尔和代数定义，函数g可以用lambda演算来定义。
但是，g自身仍然不是递归的；为了使用g来建立递归函数，作为参数传递给g的f函数必须有特殊的性质。也就是说，作为参数传递的f函数必须展开为调用带有一个参数的函数g -- 并且这个参数必须再次f函数!
换句话说，f必须展开为g(f)。这个到g的调用将接着展开为上面的阶乘函数并计算下至另一层递归。在这个展开中函数f将再次出现，并将被再次展开为g(f)并继续递归。这种函数，这里的f = g(f)，叫做g的不动点，并且它可以在lambda演算中使用叫做悖论算子或不动点算子来实现，它被表示为Y -- Y组合子：
- Y = λg.(λx.g(x x))(λx.g(x x))
在lambda演算中，Y g是g的不动点，因为它展开为g(Y g)。现在，要完成我们对阶乘函数的递归调用，我们可以简单的调用 g(Y g)n，这里的n是我们要计算它的阶乘的数。
比如假定n = 5，它展开为：
- (λn.(if n = 0 then 1 else n·((Y g)(n-1)))) 5
- if 5 = 0 then 1 else 5·(g(Y g，5-1))
- 5·(g(Y g)4)
- 5·(λn.(if n = 0 then 1 else n·((Y g)(n-1))) 4)
- 5·(if 4 = 0 then 1 else 4·(g(Y g，4-1)))
- 5·(4·(g(Y g)3))
- 5·(4·(λn.(if n = 0 then 1 else n·((Y g)(n-1))) 3))
- 5·(4·(if 3 = 0 then 1 else 3·(g(Y g，3-1))))
- 5·(4·(3·(g(Y g)2)))
- ...
等等，递归的求值算法的结构。所有递归定义的函数都可以看作某个其他适当的函数的不动点，因此，使用Y所有递归定义的函数都可以表达为lambda表达式。特别是，我们现在可以明晰的递归定义自然数的减法、乘法和比较谓词。
四 各种数据结构
各种数据结构的表示，例如，线性表，树，快排等的实现。请参考byvoid同学的讲稿：http://www.byvoid.com/blog/apio-fp/#more-3200
本文总结摘抄自：1 函数式编程
http://zh.wikipedia.org/wiki/%E5%87%BD%E6%95%B8%E7%A8%8B%E5%BC%8F%E8%AA%9E%E8%A8%80
2 lambda演算 http://zh.wikipedia.org/wiki/%CE%9B%E6%BC%94%E7%AE%97
3邱奇数 http://zh.wikipedia.org/wiki/%E9%82%B1%E5%A5%87%E6%95%B0
4 byvoid同学的讲稿：http://www.byvoid.com/blog/apio-fp/#more-3200
5 函数式编程初探 -阮一峰: http://www.ruanyifeng.com/blog/2012/04/functional_programming.html